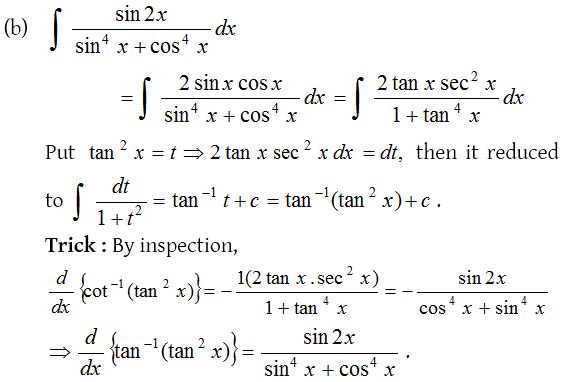Integration by Substitution
Integration by Substitution
(1) When integrand is a function i.e.,∫f[?(x)] ?'(x) dx:
Here, we put ?(x)=t, so that ?'(x) dx=dt and in that case the integrand is reduced to ∫f(t) dt.
(2) When integrand is the product of two factors such that one is the derivative of the others i.e., I = ∫f(x)f'(x) dx:
In this case we put f(x)=t and convert it into a standard integral.
(3) Integral of a function of the form f(ax + b):
Here we put ax + b = t and convert it into standard integral. Obviously if ∫f(x) dx = ?(x) then ∫f(ax + b) dx = \(\frac { 1 }{ a }\) ?(ax + b) + c.
(4) If integral of a function of the form \(\frac { f'(x) }{ f(x) }\)
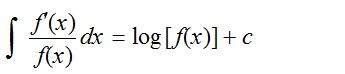
(5) If integral of a function of the form \({ [f(x)] }^{ n }f'(x)\)
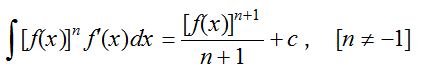
(6) If the integral of a function of the form \(\frac { f'(x) }{ \sqrt { f(x) } } \)
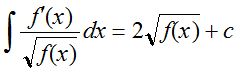
(7) Standard substitutions

Integration by Substitution Problems with Solutions
1.

Solution:
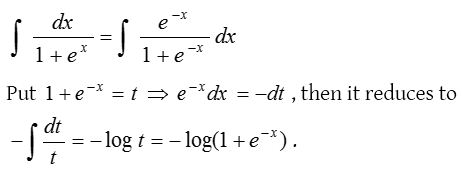
2.
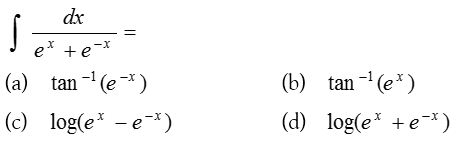
Solution:
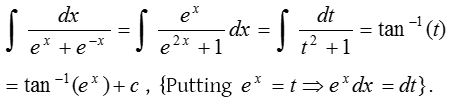
3.
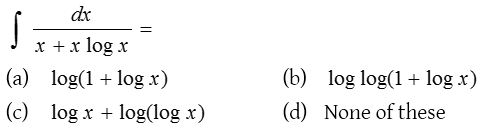
Solution:

4.
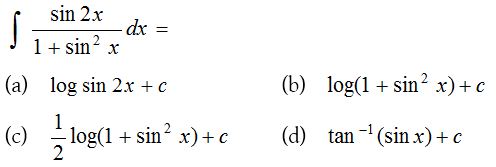
Solution:
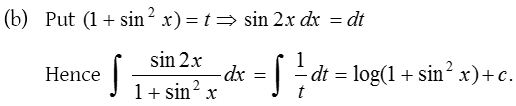
5.
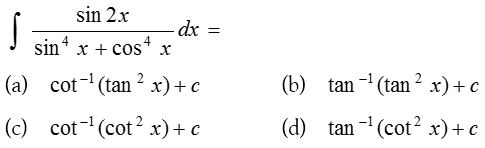
Solution: