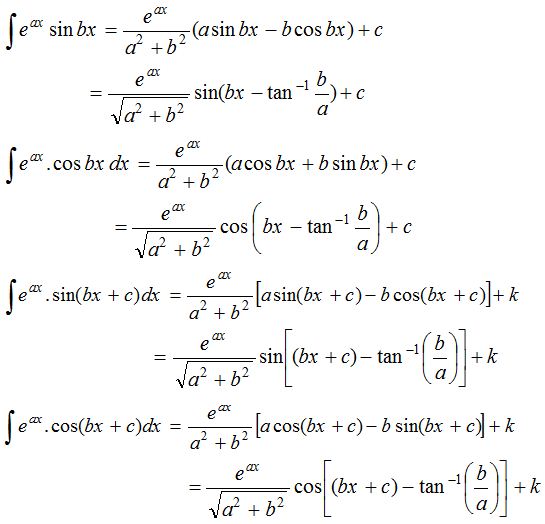Integration by Parts

Integration by Parts

(1) When integrand involves more than one type of functions:
We may solve such integrals by a rule which is known as integration by parts. We know that,

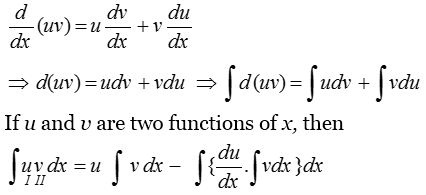
i.e., the integral of the product of two functions = (First function) × (Integral of second function) – Integral of {(Differentiation of first function) × (Integral of second function)}
Before applying this rule proper choice of first and second function is necessary. Normally we use the following methods :

1. In the product of two functions, one of the function is not directly integrable (i.e., log|x|, sin^-1x, cos^-1x, tan^-1x……etc), then we take it as the first function and the remaining function is taken as the second function.
2. If there is no other function, then unity is taken as the second function e.g. in the integration of ∫sin^-1x dx, ∫log x dx, 1 is taken as the second function.
3. If both of the function are directly integrable then the first function is chosen in such a way that the derivative of the function thus obtained under integral sign is easily integrable. Usually, we use the following preference order for the first function.
   (Inverse, Logarithmic, Algebraic, Trigonometric, Exponential). This rule is simply called as “ILATE”.

(2) Integral is of the form ∫e^x {f(x)+f‘(x)} dx:
If the integral is of the form ∫e^x {f(x)+f‘(x)} dx then by breaking this integral into two integrals integrate one integral by parts and keeping other integral as it is, by doing so, we get

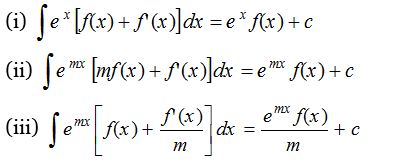
(3) Integral is of the form ∫[x f‘(x)+f(x)] dx:
If the integral is of the form ∫[x f‘(x)+f(x)] dx then by breaking this integral into two integrals, integrate one integral by parts and keeping other integral as it is, by doing so, we get,
∫[x f‘(x)+f(x)] dx = x f(x) + c

(4) Integrals of the form ∫e^ax sin bx dx ∫e^ax cos bx dx: