ICSE Maths Previous Year Question Paper 2008 Solved for Class 10
ICSE Paper 2008
MATHEMATICS
(Two hours and a half)
Answers to this Paper must be written on the paper provided separately.
You will not be allowed to write during the first 15 minutes.
This time is to be spent in reading the question paper.
The time given at the head of this Paper is the time allowed for writing the answers.
Attempt all questions from Section A and any four questions from Section B.
All working, including rough work, must be clearly shown and must be done on the same sheet as the rest of the answer. Omission of essential working will result in the loss of marks.
The intended marks for questions or parts of questions are given in brackets [ ].
Mathematical tables are provided.
SECTION-A (40 Marks)
(Attempt all questions from this Section)
Question 1:
(a) The simple interest on a sum of money for 2 years at 4% per annum is Rs. 340. Find:
(i) the sum of money and
(ii) the compound interest on this sum for one year payable half yearly at the same rate. [3]
![]()
(c) If (x – 2) is a factor of 2x3 – x2 – px – 2
(i) find the value of p.
(ii) with the value of p, factorize the above expression completely. [4]
Solution:
(a)

(b)

(c)
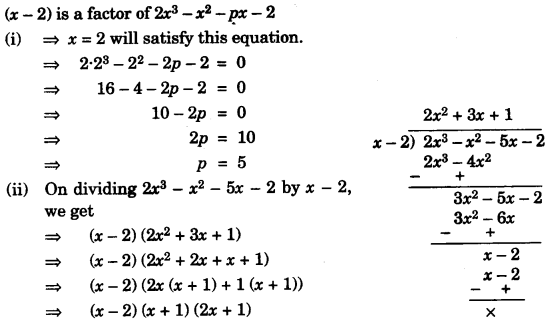
Question 2:
(a) Solve the given inequation and graph the solution on the number line.
2y – 3 < y + 1 ≤ 4y + 7; y ∈ R. [3]
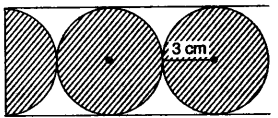
(b) In the given figure, find the area of the unshaded portion within the rectangle. (Take π = 3.14) [3]
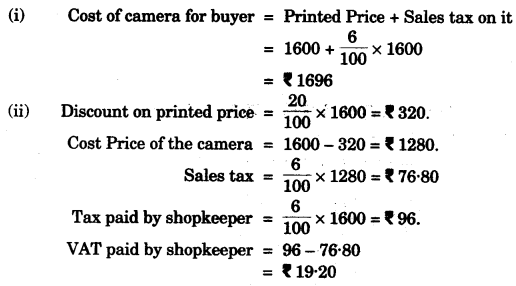
(c) A shopkeeper buys a camera at a discount of 20% from the wholesaler, the printed pried of the camera being Rs. 1600 and the rate of sales tax is 6%. The shopkeeper sells it to the buyer at the printed price and charges tax at the same rate. Find:
(i) The price at which the camera can be bought.
(ii) The VAT (Value Added Tax) paid by the shopkeeper. [4]
Solution:
(a)
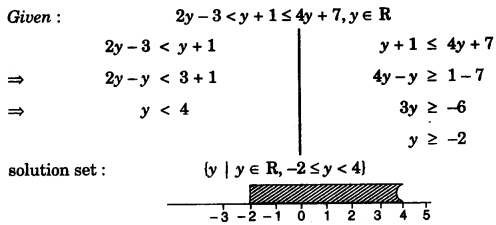
(b)


(c)
Question 3:
(a) David opened a Recurring Deposit Account in a bank and deposited Rs. 300 per month for two years. If he received Rs. 7725 at the time of maturity, find the rate of interest per annum. [3]
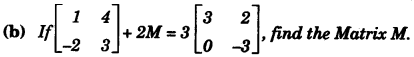 [3]
[3]
(c) Use a graph paper for this question. (Take 1 cm = 1 unit on both the axes). Plot the points A (-2, 0), B (4, 0), C (1, 4) and D (-2, 4).
(i) Draw the line of symmetry of A ABC. Name it L1.
(ii) Point D is reflected about the Line L1 to get the image E. Write the coordinates of E.
(iii) Name the figure ABED.
(iv) Draw all the lines of symmetry of the figure ABED. [4]
Solution:
(a)
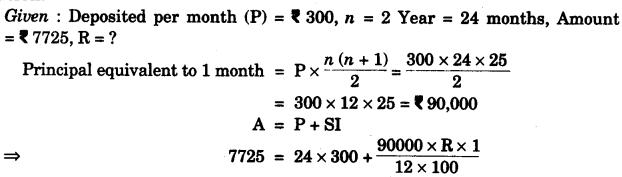
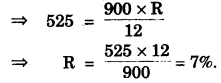
(b)
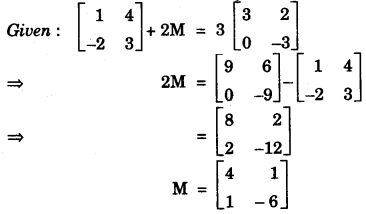
(c)
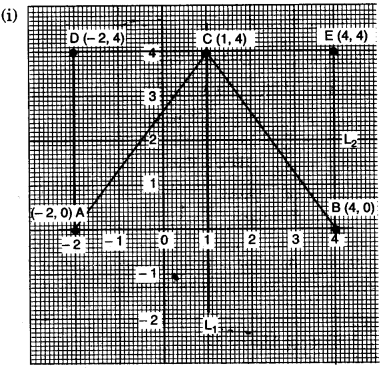
(ii) Co-ordinate of E (4, 4)
(iii) ABED is rectangle.
(iv) See figure (L1 and L2 are the line of symmetry of ractangle ABED)
Question 4:
![]()
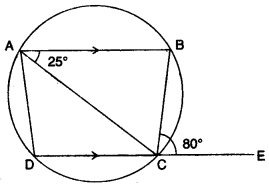
(b) In the alongside figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°. Find:
(i) ∠CAD,
(ii) ∠CBD,
(iii) ∠ADC. [3]
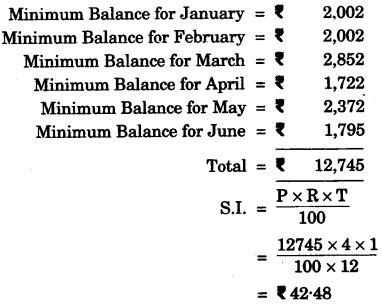
(c) Mr. Dhoni has an account in the Union Bank of India. The following entries are from his pass book:
| Date | Particulars | Withdrawals (in Rs.) | Deposits (in Rs.) | Balance (in Rs.) |
| Jan 3, 07 | B/F | — | — | 2642.00 |
| Jan 16 | To Self | 640.00 | — | 2002.00 |
| March 5 | By Cash | — | 850.00 | 2852.00 |
| April 10 | To Self | 1130.00 | — | 1722.00 |
| April 25 | By Cheque | — | 650.00 | 2372.00 |
| June 15 | By Cash | 577.00 | — | 1795.00 |
Calculate the interest from January 2007 to June 2007 at the rate of 4% per annum. [4]
Solution:
(a)

(b)
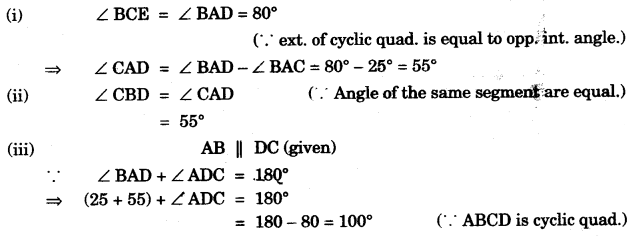
(c)
SECTION-B (40 Marks)
(Attempt any four questions from this Section)
Question 5:
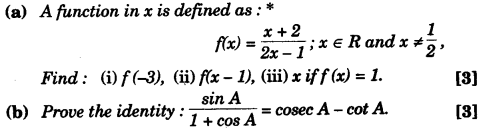
(c) If A = (-4, 3) and B = (8, -6)
(i) Find the length of AB.
(ii) In what ratio is the line joining AB, divided by the x-axis?
Solution:
(b)
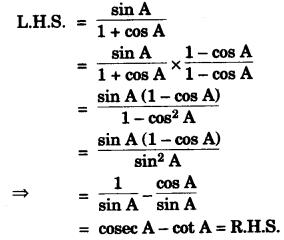
(c)
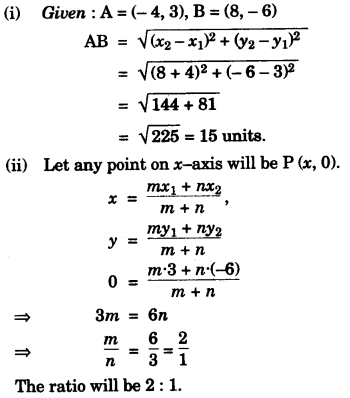
Question 6:
(a) Solve the following quadratic equation for x and give your answer correct to two decimal places:
5x (x + 2) = 3. [3]
(b)
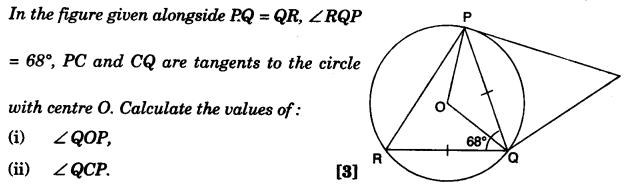
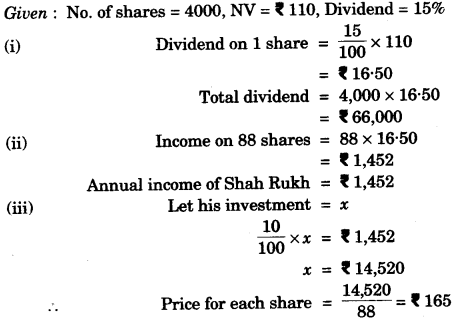
(c) A company with 4000 shares of nominal value of Rs. 110 each declares an annual dividend of 15%. Calculate:
(i) The total amount of dividend paid by the company.
(ii) The annual income of Shah Rukh who holds 88 shares in the company.
(iii) If he received only 10% on his investment, find the price Shah Rukh paid for each share. [4]
Solution:
(a)
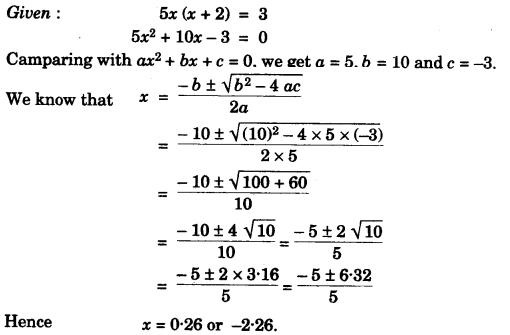
(b)

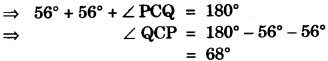
(c)
Question 7:
(a)
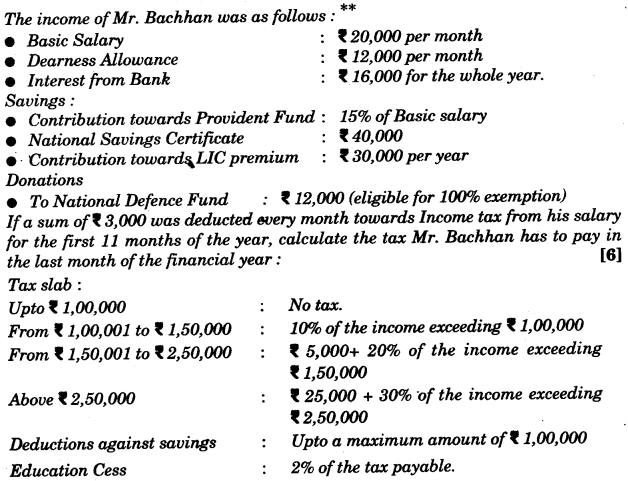
(b) A vertical pole and a vertical tower are on the same level ground. From the top of the pole the angle of elevation of the top of the tower is 60° and the angle of depression of the foot of the tower is 30°. Find the height of the tower if the height of the pole is 20 m. [4]
** Solution has not given due to out of present syllabus.
Solution:
(b) Let h be the height of tower and x be the distance between tower and pole.
Question 8:
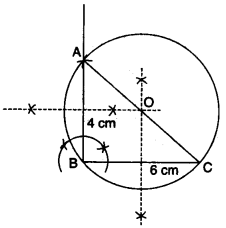
(b) Using a ruler and a pair of compasses only, construct:
(i) A triangle ABC, given AB = 4 cm, BC = 6 cm and ∠ABC = 90°.
(ii) A circle which passes through the points A, B and C and mark its centre as O. [3]
(c) Points A and B have coordinates (7, -3) and (1, 9) respectively. Find:
(i) The slope of AB.
(ii) The equation of the perpendicular bisector of the line segment AB.
(iii) The value of ‘p’ if (-2, p) lies on it. [4]
Solution:
(b) Steps of Construction:
(1) Draw side BAC, 6 cm.
(2) Draw a ∠B = 90°, and cut AB = 4 cm.
(3) Meet AC.
(4) Draw Bisector of BC and AB. Which meet at point ‘O’.
(5) Now draw a circle as centre ‘O’.
(6) This circle passes through the point A, B, and C.
(c)
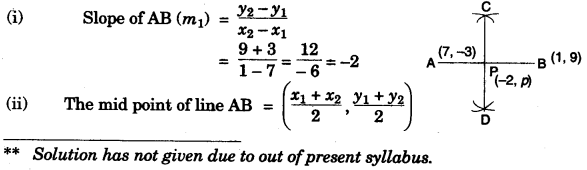

Question 9:
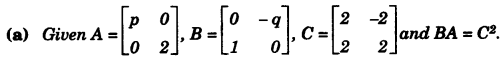
Find the values of p and q. [3]
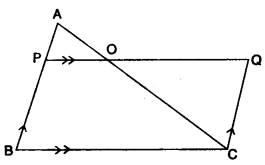
(b) In ∆ABC, AP : PB = 2 : 3. PO is parallel to BC and is extended to Q so that CQ is parallel to BA. Find:
(i) Area ∆APO : area ∆ABC.
(ii) Area ∆APO : area ∆CQO. [3]
(c) The volume of a conical tent is 1232 m3 and the area of the bare floor is 154 m2. Calculate the:
(i) Radius of the floor.
(ii) Height of the tent.
(iii) Length of the canvas required to cover this conical tent if its width is 2 m. [4]
Solution:
(a)
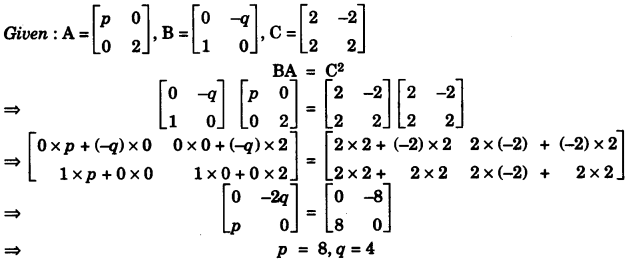
(b)

(c)


Question 10:
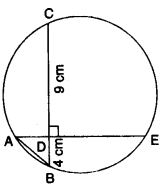
(a) In the given figure, AE and BC intersect each other at point D. If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm, find DE. [3]
(b) A straight line AB is 8 cm long. Locate by construction the locus of a point which is:
(i) Equidistant from A and B.
(ii) Always 4 cm from the line AB.
(iii) Mark two points X and Y, which are 4 cm from AB and equidistant from A and B, Name the figure AXBY. [3]
(c) Some students planned a picnic. The budget for the food was Rs. 480. As eight of them failed to join the party, the cost of the food for each member increased by Rs. 10. Find how many students went for the picnic. [4]
Solution:
(a)
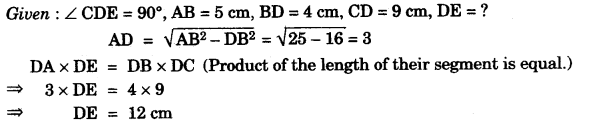
(b) Steps of Construction:
(i) Draw AB is 8 cm, Draw PQ the perpendicular bisector of AB.
(ii) Draw CD and EF both parallel to AB and each at a distance of 4 cm from AB.
(iii) AXBY is a square.
(c)
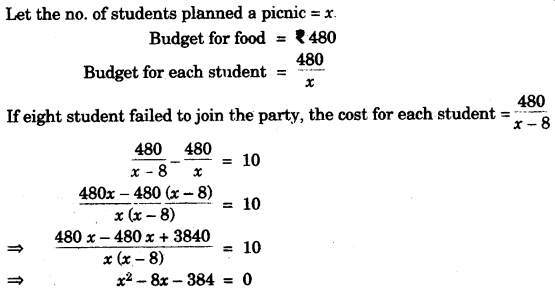
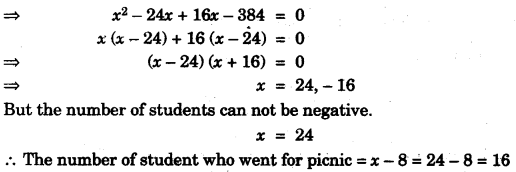
Question 11:
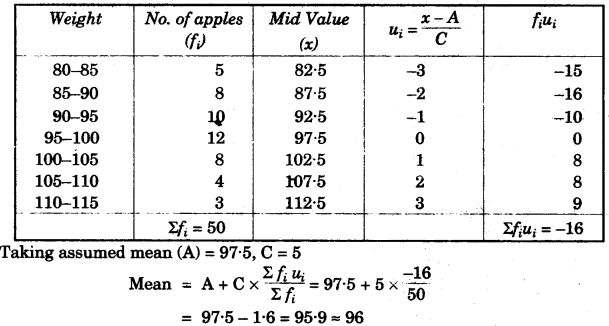
(a) The weight of 50 apples were recorded as given below. Calculate the mean weight, to the nearest gram, by the Step Deviation Method. [5]
| Weight in grams | 80-85 | 85-90 | 90-95 | 95-100 | 100-105 | 105-110 | 110-115 |
| No. of apples | 5 | 8 | 10 | 12 | 8 | 4 | 3 |
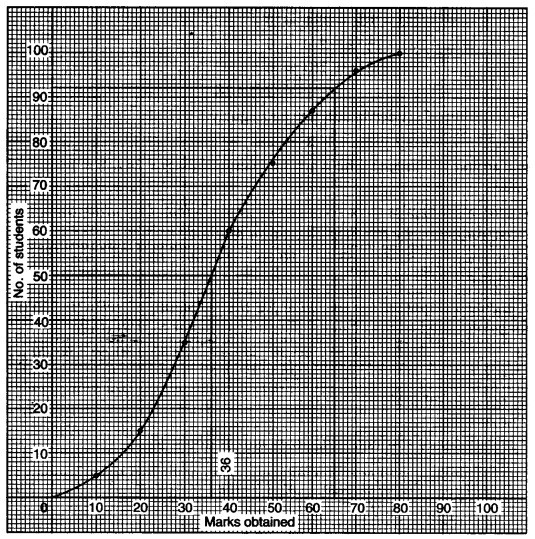
(b) Using a graph paper, draw an ogive for the following distribution which shows the marks obtained in the General Knowledge paper by 100 students.
| Marks | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 |
| No. of students | 5 | 8 | 20 | 25 | 15 | 12 | 9 | 4 |
Use the ogive to estimate:
(i) The median.
(ii) The number of students who score marks above 65. [5]
Solution:
(a)
(b)
| Marks | No. of students | c.f. |
| 0-10 | 5 | 5 |
| 10-20 | 10 | 15 |
| 20-30 | 20 | 35 |
| 30-40 | 25 | 60 |
| 40-50 | 15 | 75 |
| 50-60 | 12 | 87 |
| 60-70 | 9 | 96 |
| 70-80 | 4 | 100 |
| 100 |