ICSE Maths Previous Year Question Paper 2007 Solved for Class 10
ICSE Paper 2007
MATHEMATICS
(Two hours and a half)
Answers to this Paper must be written on the paper provided separately.
You will not be allowed to write during the first 15 minutes.
This time is to be spent in reading the question paper.
The time given at the head of this Paper is the time allowed for writing the answers.
Attempt all questions from Section A and any four questions from Section B.
All working, including rough work, must be clearly shown and must be done on the same sheet as the rest of the answer. Omission of essential working will result in the loss of marks.
The intended marks for questions or parts of questions are given in brackets [ ].
Mathematical tables are provided.
SECTION-A (40 Marks)
(Attempt all questions from this Section)
Question 1:
(a) Show that (x – 1) is a factor of x3 – 7x2 + 14x – 8. Hence, completely factorise the above expression. [3]
(b) Dinesh bought an article for f 374, which included a discount of 15% on the marked price and a sales tax of 10% on the reduced price. Find the marked price of the article. [3]
(c) Ramesh invests 112,800 for three years at the rate of 10% per annum compound interest. Find:
(i) The sum due to Ramesh at the end of the first year.
(ii) The interest he earns for the second year.
(iii) The total amount due to him at the end of the third year. [4]
Solution:

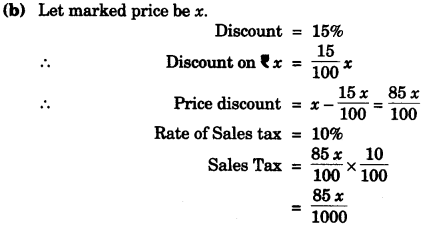


Question 2:
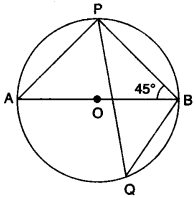
(a) In the given figure, O is the centre of the circle and ∠PBA = 45°. Calculate the value of ∠PQB. [3]
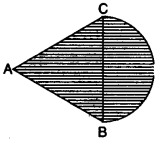
(b) In an equilateral ∆ ABC of side 14 cm, side BC is the diameter of a semi-circle as shown in the figure below. Find the area of the shaded region. [3]
(take π = 22/7 and y (√3 = 1.732)
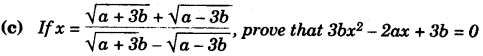
Solution:
(a) ∠AOB = 180°
⇒ ∠APB = 90° (angle of diameter)
⇒ ∠PAB = 90° – 45° = 45°
⇒ ∠PQB = 45° (angle for same arc)


Question 3:
(a) If 2\(\begin{bmatrix} 3 & 4 \\ 5 & x \end{bmatrix}\) + \(\begin{bmatrix} 1 & y \\ 0 & 1 \end{bmatrix}\) = \(\begin{bmatrix} 7 & 0 \\ 10 & 5 \end{bmatrix}\). Find the values of x and y. [3]
(b) Solue following inequation and graph the solution on the number line: [3]
![]()
(c) Use a graph paper for this question.
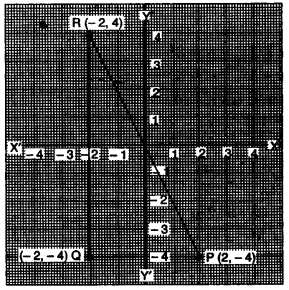
(i) The point P (2,- 4) is reflected about the line x = 0 to get the image Q. Find the co-ordinates of Q.
(ii) Point Q is reflected about the line y = 0 to get the image R. Find the co-ordinates of R.
(iii) Name the figure PQR.
(iv) Find the area of figure PQR. [4]
Solution:
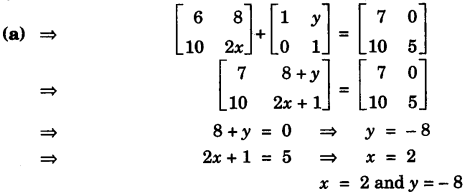

(c) (i) Q (-2, -4)
(ii) R (-2, 4)
(iii) Right angle triangle.
(iv) Area of A PQR = \(\frac { 1 }{ 2 } \) × 4 × 8
= 16 sq. unit
Question 4:
![]()
(b) Saloni deposited Rs.150 per month in her bank for eight months under the Recurring Deposit Scheme. What will be the maturity value of her deposit, if the rate of interest is 8% per annum and the interest is calculate at the end of every month. ? [3]
(c) Find the mean of the following distribution: [4]
| Class Interval | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 |
| Frequency | 10 | 6 | 8 | 12 | 5 |
Solution:

(c)
| Class Interval | f | x | d = x – A | fd |
| 0-10 | 10 | 5 | -20 | -200 |
| 10-20 | 6 | 15 | -10 | -60 |
| 20-30 | 8 | 25 = A | 0 | 0 |
| 30-40 | 12 | 35 | 10 | 120 |
| 40-50 | 5 | 45 | 20 | 100 |
| N = Σf =41 | Σfd = -40 |
Mean = A + Σfd/N = 25 + (-40)/41 = 25 – 0.97 = 24.03
SECTION-B (40 Marks)
(Attempt any four questions from this Section)
Question 5:
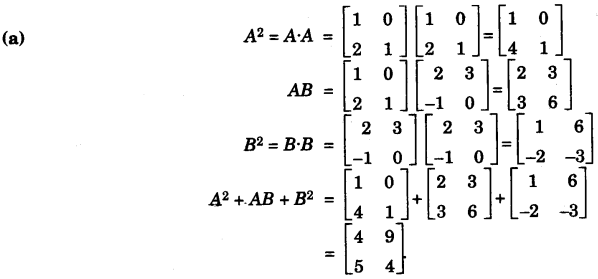
(a) Let A = \(\begin{bmatrix} 1 & 0 \\ 2 & 1 \end{bmatrix}\), B = \(\begin{bmatrix} 2 & 3 \\ -1 & 1 \end{bmatrix}\). Find A2 + AB + B2. [3]
(b) Ajay owns 560 shares of a company. The face value of each share is Rs. 25. The company declares a dividend of 9%. Calculate:
(i) The dividend that Ajay will get.
(ii) The rate of interest on his investment, if Ajay had paid Rs. 30 for each share. [3]
(c) The surface area of a solid metallic sphere is 616 cm2. It is melted and recast into smaller spheres of diameter 3.5 cm. How many such spheres can he obtained ? [4]
Solution:

Question 6:
(a) Mr. Ashok Sharma’s income from his salary in the year 2005-06 was Rs. 2,96,000.
Savings:
Contribution towards Provident Fund: Rs. 1,500 per month
Contribution towards L.I.C. premium: Rs. 10,000 per month
National Saving Certificates Donations: Rs. 15,000 per month
Donations:
To Prime Minister’s Relief Fund : Rs. 12,000 (eligible for 100%tax exemption)
If a sum of Rs. 4,000 was deducted every month towards Income Tax from his salary for the first 11 months of the year, calculate Mr. Sharma’s income tax liability in the last month of the year.
Tax Slab:
Upto Rs. 50,000: Notax
Rs. 50,001 to Rs. 60,000: 10% of income exceeding Rs. 50,000
Rs. 60,001 to Rs. 1,50,000: Rs. 1,000 + 20% of the income exceeding Rs. 60,000
Above Rs. 1,50,000: Rs. 19,000 +30% of the income exceeding Rs. 1,50,000
Standard Deduction: Rs.20,000
Rebate in tax: 20% of the total savings or Rs. 14,000 whichever is less
Surcharge: 10% of the total tax payable after rebate. [6]
(b) Five years ago, a woman’s age was the square of her son’s age. Ten years hence her age will be twice that of her son’s age. Find:
(i) The age of the son five years ago.
(ii) The present age of the women. [4]
Solution:
(a) Solution has not given due to out of present syllabus.

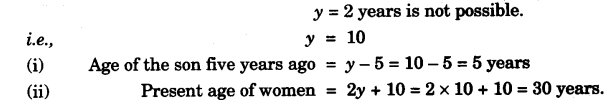
Question 7:
(a) Solve the following quadratic equation for x and give your answer correct to two decimal places:
x2-3x -9 = 0 [3]
(b) Using a ruler, construct a triangle ABC with BC = 6.4 cm, CA = 5.8 cm and ∠ABC = 60°. Draw its incircle. Measure and record the radius of the incircle. [3]
(c) Mrs. Kumar has an account with The Bank of India. The following entries are from her pass book:
| Date | Particulars | Withdrawals Rs. | Deposits Rs. | Balance Rs. |
| 08.02.06 | B/F | — | — | 8500.00 |
| 18.02.06 | To self | 4000.00 | — | — |
| 12.04.06 | By cash | — | 2238.00 | — |
| 15.06.06 | To self | 5000.00 | — | — |
| 08.07.06 | By cash | — | 6000.00 | — |
Complete the above page of her pass book and calculate the interest for the six months, February to July 2006, at 4.5% per annum. [4]
Solution:

(b) Steps of Constructions:

- Draw BC = 6.4 and at B angle 60°.
- Taking C as centre cut AC = 5.8 cm on the arm XB.
- Draw angle bisector of ∠ACB and ∠ABC which intersect at O.
- Taking O as centre. Draw a incircle.
- Draw 1 from O on BC which cut at M.
- Required radius of incircle OM = 1.5 cm.
(c)
| Date | Particulars | Withdrawals Rs. | Deposits Rs. | Balance Rs. |
| 08.02.06 | B/F | — | — | 8500.00 |
| 18.02.06 | To self | 4000.00 | — | 4500.00 |
| 12.04.06 | By cash | — | 2238.00 | 6738.00 |
| 15.06.06 | To self | 5000.00 | — | 1738.00 |
| 08.07.06 | By cash | — | 6000.00 | 7738.00 |

Question 8:
![]()
(b) The mid point of the line segment joining (2a, 4) and (-2, 2b) is (1, 2a + 1). Find the values of a and b. [3]
(c) In the given figure, if ∠ACE = 43° and ∠CAF = 62° find the values of a, b and c. [4]

Solution:


Question 9:

(b) Find the equation of the line parallel to the line 3x + 2y = 8 and passing through the point (0,1). [3]
(c) From the top of a hill, the angles of depression of two consecutive kilometer stones, due east are found to be 30° and 45° respectively. Find the distance of the two stones from the foot of the hill. [4]
Solution:
(a) Solution has not given due to out of present syllabus.



Question 10:
(a) The table below shows the distribution of the scores obtained by 120 shooters in a shooting competition. Using a graph sheet, draw an ogive for the distribution.
| Scores obtained | 0-10 | 10-20 | 20-30 | 30-10 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
| Number of Shooters | 5 | 9 | 16 | 22 | 26 | 18 | 11 | 6 | 4 | 3 |
Use your ogive to estimate:
(i) The Median.
(ii) The inter quartile range.
(iii) The number of shooters who obtained more than 75% scores. [6]
(b) In the given figure, ABC is a triangle. DE is parallel to BC and \(\frac { AD }{ DB } =\frac { 3 }{ 2 }\).
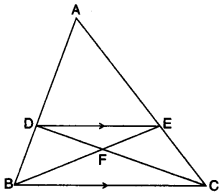
(i) Determine the ratios \(\frac { AD }{ DB }\), \(\frac { DE }{ BC }\).
(ii) Prove that ∆DEF is similar to ∆CBF. Hence, find \(\frac { EF }{ FB }\).
(iii) What is the ratio of the areas of ∆DFE and ∆BFC ? [4]
Solution:
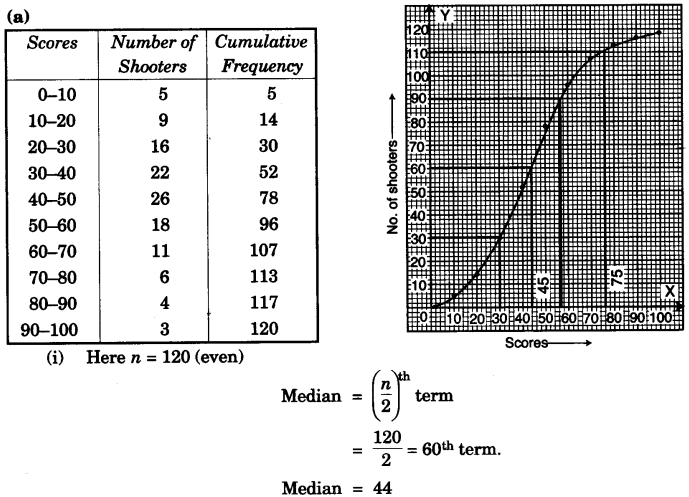

(iii) The number of shooters when obtained more than 75% scores. From E draw a vertical line to meet ogive at F. From F draw horizontal line to D
= 120 – 110 = 10


Question 11:
(a) If the line joining the points A (4, – 5) and B (4, 5) is divided by the point P such that \(\frac { AP }{ AB } =\frac { 2 }{ 5 }\), find the co-ordinates of P. [3]
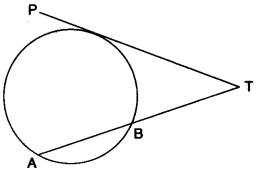
(b) In the figure given, PT is a tangent to the circle.
Find PT if AT = 16 cm and AB = 12 cm. [3]
(c) Construct a triangle BCP given BC = 5 cm, BP = 4 cm and ∠PBC = 45°.
(i) Complete the rectangle ABCD such that:
(1) Pis equidistant from AB and BC.
(2) P is equidistant from C and D.
(ii) Measure and record the length of AB. [4]
Solution:

(c) Steps of Constructions:

(i) Draw a line BC = 5 cm and make an angle of 45° at B.
(ii) Cut an arc of 4 cm from B at P.
(iii) Make an angle of 90° at B and draw a line || to BC from P. Which cuts the line of 90° angle from B at R.
(iv) Cut RB = RA and Mark D at PC = PD
(v) Complete the rectangle ABCD of length AB = 6-5 cm.