ICSE Maths Question Paper 2018 Solved for Class 10

ICSE Maths Previous Year Question Paper 2018 Solved for Class 10

General Instructions :

• Answers to this Paper must be written on the paper provided separately.
• You will not be allowed to write during the first 15 minutes.
• This time is to be spent in reading the question paper.
• The time given at the head of this Paper is the time allowed for writing the answers.
• Attempt all questions from Section A and any four questions from Section B.
• All working, including rough work, must be clearly shown and must be done on the same sheet as the rest of the answer.
• Omission of essential working will result in the loss of marks.
• The intended marks for questions or parts of questions are given in brackets [ ].
• Mathematical tables are provided.
  

Section A [40 marks]
(Answer all questions from this Section.)

Question 1.
(a) Find the value of x’ and y’ if : [3]

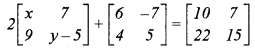
(b) Sonia had a recurring deposit account in a bank and deposited 3600 per month for 244 years. If the rate of interest was 10% p.a., find the maturity value of this account. [3]
(c) Cards bearing numbers 2, 4, 6, 8, 10, 12, 14, 16, 18 and 20 are kept in a bag. A card is drawn at random from the bag. Find the probability of getting a card which is : [4]
(i) a prime number.
(ii) a number divisible by 4.
(iii) a number that is a multiple of 6.
(iv) an odd number.
Answer:

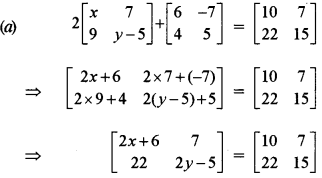
⇒ 2 JC + 6 = 10 ⇒ 2x = 4 ⇒ x = 2
And 2y – 5 = 15 ⇒ 2y = 20 ⇒ y = 10
Hence, the values of x and y are x = 2 and y = 10

(b) Here, amount deposited per month = ₹ 600
Number of months = 2 x 12 + 6 = 30  [∵ v T = \(2 \frac{1}{2}\) years]
Rate of interest = 10% p.a.

Hence, the amount received by Sonia on maturity is ₹ 20325.

(c)Total number of cards in the bag = 10
(i) Total prime numbers = 1 i.e., 2
∴ Required Probability = \(\frac{1}{10}\)
(ii) Total numbers divisible by 4 = 5 (i.e., 4, 8, 12, 16, 20]
Required Probability = \(\frac{5}{10}\) = \(\frac{1}{2}\)
(iii) Total numbers divisible by 6 or multiple of 6 = 3 [i.e., 6, 12, 18]
∴ Required Probability = \(\frac{3}{10}\)
(iv) Total odd number = 0
∴ Required Probability = \(\frac{0}{10}\) = 0.

Question 2.
(a)The circumference of the base of a cylindrical vessel is 132 cm and its height is 25 cm. Find the :
(i) radius of the cylinder
(ii) volume of cylinder, (use π = \(\frac{22}{7}\)) [3]
(b) If (k – 3), (2k + 1) and (4k + 3) are three consecutive terms of an A.P., find the value of k.
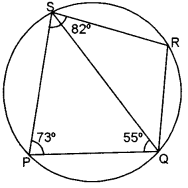
(c) PQRS is a cyclic quadrilateral. Given ∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82 °, calculate: [4]
(i) ∠QRS
(ii) ∠RQS
(iii) ∠PRQ

Answer :
(a) Let r be the radius of the base of cylindrical vessel and ft = 25 cm be its height.
Now, circumference of the base = 132 cm
2πr = 132

Hence, the radius of the cylinder is 21 cm and volume of the cylinder is 34650 cm³

(b) Here, ft – 3, 2k + 1 and 4k + 3 are three consecutive terms of an A.P.
∴ 2k + 1 – (k – 3) = 4k + 3 – (2k + 1)
⇒ 2k + 1 – k + 3 = 4k + 3 – 2k – 1
⇒ k + 4 = 2k + 2
⇒ 2k – k =4 – 2
⇒ k = 2
Hence, the value of ft is 2.

(c) (i) Since PQRS is a cyclic quadrilateral
∠QPS + ∠QRS – 180°
⇒ 73° + ∠QRS = 180°
⇒ ∠QRS = 180° – 73°
∠QRS = 107°
(ii) Again, ∠PQR + ∠PSR = 180°
∠PQS + ∠RQS + ∠PSR = 180°
55° – ∠RQS + 82° = 180°
∠RQS = 180° – 82° – 55° = 43°
(iii) In ∆PQS, by using angles sum property of a ∆.
∠PSQ + ∠SQP + ∠QPS = 180°
∠PSQ + 55° + 73° = 180°
∠PSQ = 180° – 55° – 73°
∠PSQ = 52°
Now, ∠PRQ = ∠PSQ = 52° [Oop. ∠s of the same segment]
Hence, ∠QRS = 107°, ∠RQS = 43° and
∠PRQ = 52°

Question 3.
(a) If (x + 2) and (x + 3) are factors of x³ + ax + b, find the values of ‘a’ and ‘b’. [3]
(b) Prove that  [3]
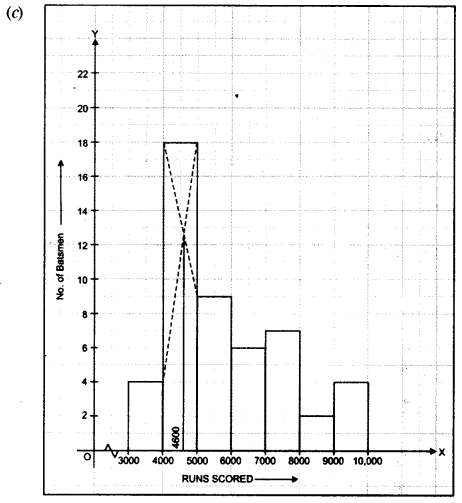
(c) Using a graph paper draw a histogram for the given distribution showing the number of runs scored by 50 batsmen. Estimate the mode of the data : [4]

Answer :
(a) Given that (x + 2) and (x + 3) are factors of p(x) = x³ + ax + b.
∴ p(- 2) = (- 2)³ + o(- 2) + b = 0
⇒ – 8 – 2a + b = 0 => – 2a + b = 8 …….(i)
And p(- 3) = (- 3)³ + a(- 3) + b = 0
⇒ – 27 – 3a + b = 0 => – 3a + b = 27 ……..(ii)
Subtracting (i) from (ii), we obtain
(- 3a 4 – b) – (- 2a + b) = 27 – 8
– 3a + b + 2a – b = 19
-a = 19
⇒ a = 19
From (i), we obtain
– 2(19) + b = 8
– 38 + b = 8
⇒ b = 8 + 38
⇒ b = 46
Hence, the values of a and b are a = 19 and b = 46.

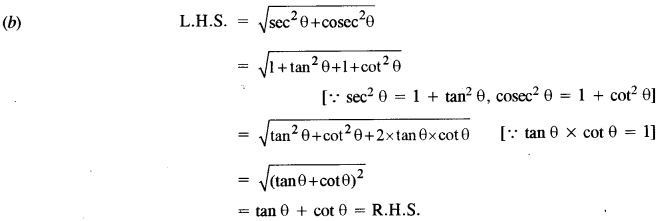
Question 4.
(a) Solve the following in equation, write down the solution set and represent it on the real number line: [3]
– 2 + 10x ≤ 13x + 10 < 24 + 10x, x ∈ Z
(b) If the straight lines 3x – 5y = 7 and 4x + ay + 9 = O are perpendicular to one another, find the value of a. [3]
(c) Solve x² + 7x = 7 and give your answer correct to two decimal places. [4]
Answer.
(a) Given that :

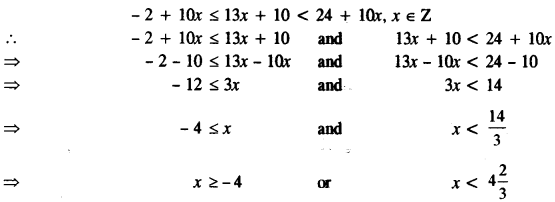
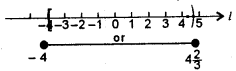
Thus, the required solution set is :

Using number line, we have

(b) Given lines are
3x – 5y = 1 ……….(i) and 4x + ay + 9 = 0  …………(ii)
Slope of line (i) (m₁) =  \(-\left(\frac{3}{-5}\right)=\frac{3}{5}\)
Slope of line (ii) (m₂) = \(-\left(\frac{4}{a}\right)\)

Also, given that two lines are perpendicular to one and another
∴ (m₁) (m₂) = – 1
⇒
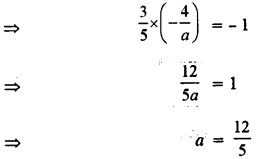
Hence, the value of a = \(\frac{12}{5}\) .

(c) Here, x² + 7x = 7
⇒ x² + 7x – 7 = 0

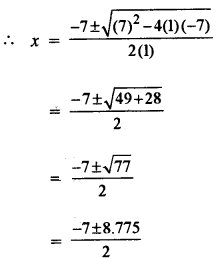
SECTION – B [40 MARKS]
(Attempt any four questions)

Question 5.
(a) The 4^th term of a G. P. is 16 and the 7^h term is 128. Find the first term and common ratio of the series. [3]
(h) A man invests ₹ 22,500 in ₹ 50 shares available at 10% discount. If the dividend paid by the company is 12%c, calculate : [3]
(i) The number of shares purchased.
(ii) The annual dividend received.
(iii) The rate of return he gets on his investment. Give your answer correct to the nearest whole number.
(c) Use graph paper for this question (Take 2 cm = 1 unit along both x and y axis). ABCD is a quadrilateral whose vertices are A(2, 2), B(2, -2), C(0, -1) and D (0,1). [4]
(i) Reflect quadrilateral ABCD on the y-axis and name it as A’B’CD.
(ii) Write down the coordinates of A’ and B’.
(iii) Name two points which are invariant under the above reflection.
(iv) Name the polygon A’B’CD.
Answer.
(a) Let a and r be the first term and common ratio of given G.P.
∴ a₄ = 16
⇒ ar³ = 16
and a₇ = 128
⇒ a⁶ = 128
Dividing (ii) and (i), we obtain

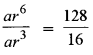
a3 = 3
a³ = 2³
a = 2
⇒
From (i), we have
2(r³) = 16
r³ = 8
r³ = 23
⇒ r = 2
Hence, the first term and common ratio of the given series is 2 and 2.

(b) Total investment = ₹ 22,500
Face value of a share = ₹ 50
Market value of a share = ₹ (50 – 10% of 50) = ₹ (50 – 5) = ₹ 45
∴ No. of shares purchased = \(\frac{22500}{45}\) = 500
Annual dividend per share = 12 % of 50
= \(\frac{12}{100} \times 50\) = ₹ 6
Total annual dividend = ₹ 6 × 500 = ₹ 3000
Rate of return =\(\frac{3000}{22500}\) × 100
= 13.3 %
= 13% (Nearest whole number)
Hence, number of shares purchased are 500, total annual dividend is ₹ 3000 and rate of return on investment is nearly 13 % p. a.
(c) Scale used is : 2 cm = 1 unit along both x and y axis.
(i) Here, vertices of the quadrilateral ABCD are A(2, 2), B(2, -2), C(0, -1) and D(0, 1)

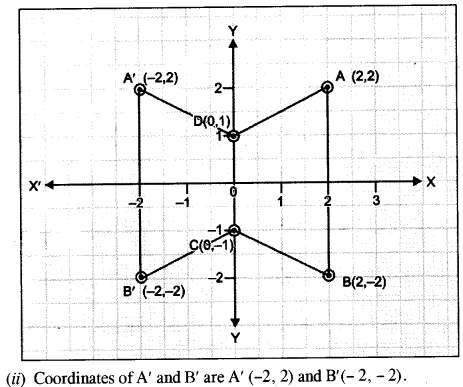
(iii) Two points which are invariant are C and D.
(iv) A’B’CD is a trapezium.

Question 6.
(a) Using properties of proportion, solve for x. Given that x is positive : [3]
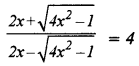[3]
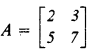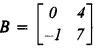(b) ,and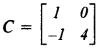, find AC + B² – 10C. [3]
(c) Prove that (1 + cot θ – cosec θ) (1 + tan θ + sec θ) = 2 [4]
Answer.

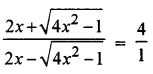
By componendo and Dividendo, we have

Squaring both sides, we have

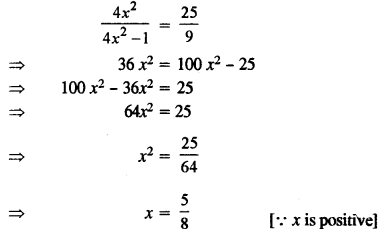
Hence the value of x is \(\frac{5}{8}\)

(b) Given that

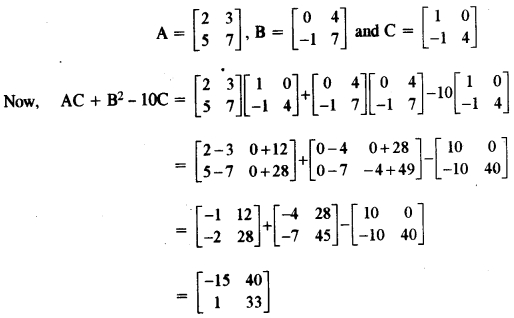
(c) L.H.S. = (1 +cot θ – cosec θ) (1 + tan θ + sec θ)

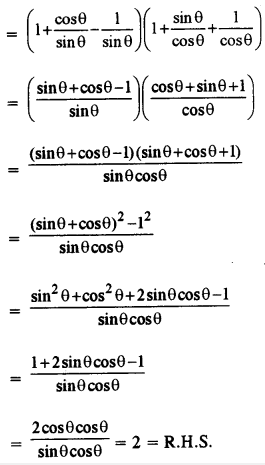
Question 7.
(a) Find the value of kfor which the following equation has equal roots. [3]
x² + 4kx + (k² – k + 2) =0
(b) On a map drawn to a scale of 1 : 50,000, a rectangular plot of land ABCD has the following daimentions AB = 6 cm;BC = 8 cm and all angles are right angles. Find :
(i) the actual length of the diagonal distance AC of the plot in km.
(ii) the actual area of the plot in sq. km.
(c) A(2, 5), B(-1, 2) and C(5, 8) are the vertices of a triangle ABC, ‘M’ is a point on AB such that AM : MB = 1:2. Find the co-ordinates of M’. Hence find the equation of the line passing through the points C and M. [4]
Answer.
(a) Given quadratic equation is :
x² + 4kx + (k² – k + 2) = 0
For equal roots, we have
b² – 4 ac = 0
⇒ (4k)2 – 4(1) (k2-k + 2) = 0
⇒ 16k² – 4k² + 4k – 8 = 0
⇒ 12k² + 4k – 8 = 0
or 3k² + k – 2 = 0
⇒ 3k² + 3k – 2k -2 = 0
⇒ 3k(k + 1) – 2(k + 1) = 0
⇒ (k + 1)(3k – 2) = 0
⇒ k + 1=0 or 3k – 2 = 0
k = – 1 or k = \(\frac{2}{3}\)

(b) Scale used on the map is 1 : 50,000
Dimensions of a rectangular plot ABCD are AB = 6 cm, BC = 8 cm Since each angle is right angle
∴ By using Pythagoras theorem, we have

(i) Actual length of the diagonal AC = 10 × 50000 cm
= \(\frac{500000}{100000}\) km
= 5 km
(ii) Area of the rectangular field ABCD on map
= 6 × 8 = 48 cm²
Actual area of the field = 48 × 500000 × 500000
= 12(10)¹⁰ sq. cm.
= 12 sq. km.

(c) Coordinates of the vertices of a ∆ ABC are A(2, 5), B(- 1, 2) and C (5, 8). Since M is a point on AB such that AM : MB = 1 : 2

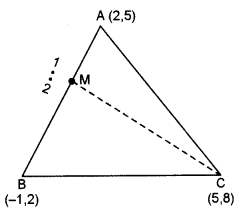
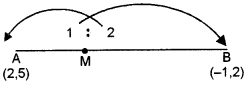
Coordinates M are

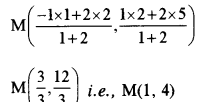
Now, equation of the line CM is given as :

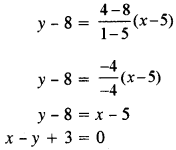
Question 8.
(a) ₹ 7500 were divided equally among a certain number of children. Had there been 20 less children, each would have received ₹ 100 more. Find the original number of children. [3]
(b) If the mean of the following distribution is 24, find the value of ‘a’. [3]

(i) Using ruler and compass only, construct a ∆ABC such that BC = 5 cm and AB = 6.5 cm and ∠ABC = 120°. [4]
(ii) Construct a circum-circle of ∆ABC.
(iii) Construct a cyclic quadrilateral ABCD, such that D is equidistant from AB and BC.
Answer.
(a) Total amount = ₹ 7500
Let the number of children be x
∴ Share of each child = ₹ \(\frac{7500}{x}\)
According to the statement

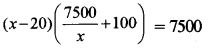
(x – 20) (7500 + 100a) = 7500 x
7500x + 100x² – 150000 – 2000x – 7500x = 0
100x² – 200x – 150000 = 0
x² – 20a – 1500 = 0
x² – 50x + 30x – 1500 = 0
x(x – 50) + 30(x – 50) = 0
(x – 50) (a + 30) = 0
⇒ a = 50 or a = – 30
Rejecting -ve value, because number of children cannot be negative.
∴ x = 50

Hence, the original number of children is 50.

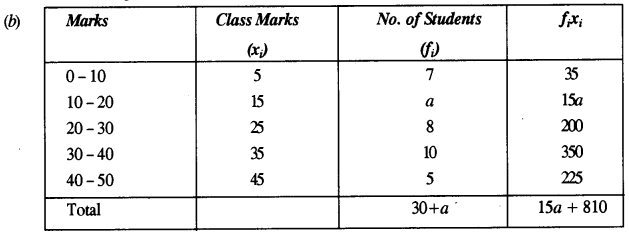
Mean = 24 (given)
∴ \(\frac{15 a+810}{30+a}\) = 24
15a + 810 = 720 + 24a
⇒ 24a – 15a = 810 – 720
⇒ 9a = 90
⇒ a = 10
Hence, the value of a is 10.

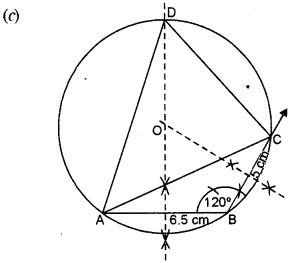
Steps of Construction :

1. Draw a line segment AB = 6.5 cm.
2. At B, construct an angle of 120° and cut off BC = 5 cm.
3. Join AC, to have ∆ABC.
4. Draw the perpendicular bisectors of line segments AB and BC.
5. Let they intersect each other in 0.
6. With 0 as centre and radius OA or OB or OC, draw the circumcircle of ∆ABC.
7. Produce perpendicular bisector of line segment AB and let it intersect the circumcircle of ∆ABC at D.
8. Join AD and CD.
   Thus, quad. ABCD is the required quadrilateral.

Question 9.
(a) Priyanka has a recurring deposit account of ₹ 1000 per month at 10% per annum. If she gets ₹ 5550 as interest at the time of maturity, find the total time for which account has held. [3]
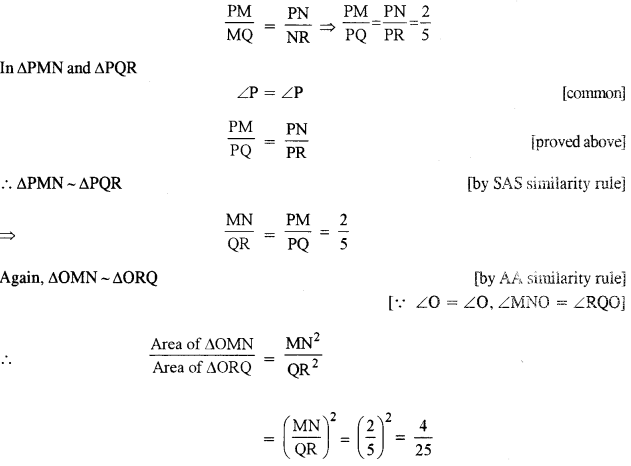
(b) In ∆ PQR, MN is parallel to QR and \(\frac{P M}{M Q}\) = \(\frac{2}{3}\) [3]

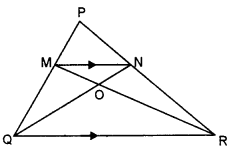
(i) Find \(\frac{M N}{Q R}\)
(ii) Prove that ∆OMN and ∆ORQ are similar.
(iii) Find, Area of ∆OMN: Area of ∆ORQ
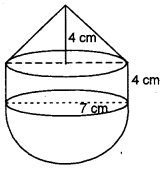
(c) The following figure represents a solid consisting of a right circular cylinder with a hemisphere at one end and a cone at the other. Their common radius is 7 The height of the cylinder and cone are each of 4 cm. Find the volume of the solid. [4]

Answer:
Amount deposited per month = ₹ 1000
Rate of interest = 10% p.a.
Interest = ₹ 5550

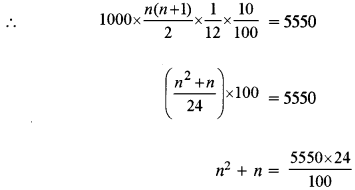
n² + n = 1332
n² + n – 1332 = 0
n² + 37n – 36n – 1332 = 0
n(n + 37) – 36(n + 37) = 0
(n – 36) (n + 37) = 0
n = 36 or n = – 37
Rejecting – ve value of n, we have n = 36
Hence, the total time for which the account was held, was 36 month or 3 years.

(c) Given that:

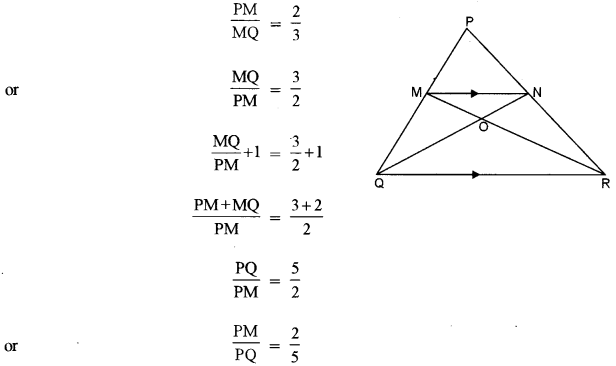
In ∆PQR, MN is parallel to QR
∴ By using Basic Proportionality theorem, we have

(c) Here, radius of cone = radius of cylinder = radius of hemisphere = 7 cm
Height of cone = 4 cm
Height of cylinder = 4 cm

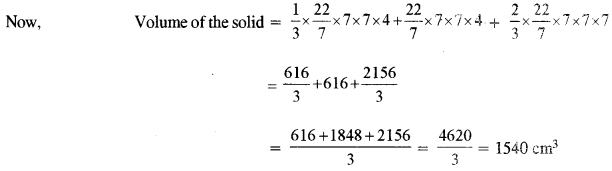
Question 10.
(a) Use Remainder theorem to factorize the following polynomial: [3]
2x³ + 3x² – 9x – 10.
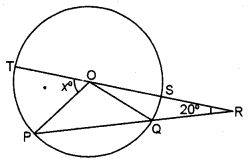
(b) In the figure given below ‘O’ is the centre of the circle. If QR = OP and ∠ORP = 20°. Find the value of ‘x ’ giving reasons. [3]

(c) The angle of elevation from a point P of the top of a tower QR, 50 m high is 60 ° and that of the tower PT from a point Q is 30°. Find the height of the tower PT, correct to the nearest metre

Answer :
(a)  Let p(x) = 2x³ + 3x² – 9x – 10
Factors of constant term 10 are ± 1, ± 2, ± 5
Put x = 2, we have
p(2) =2(2)³ + 3(2)² – 9(2) – 10
= 16 + 12 – 18 – 10
= 0
∴ (x – 2) is a factor of p(x)
Put x = – 1, we have
P(-1) =2(-1)³ + 3(-1)² – 9 (-1) – 10
= – 2 + 3 + 9 – 10 = 0
∴ (x + 1) is a factor of p(x)
Thus, (x + 1) (x – 2) i.e.,x² – x – 2 is a factor of p(x)

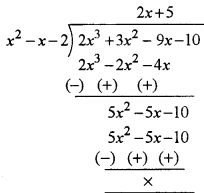
Hence, (x + 1), (x – 2) and (2x + 5) are the factors of given polynomial 2x³ + 3x² – 9x – 10.
(b) Here, in ∆OPQ
OP = OQ = r
Also, OP = QR [Given]
OP = OQ = QR = r

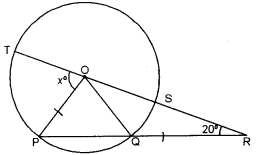
In ∆OQR, OQ = QR
∠QOR = ∠ORP = 20°
And ∠OQP = ∠QOR + ∠ORQ
= 20° + 20°
= 40°
Again, in ∆ OPQ
∠POQ = 180° – ∠OPQ – ∠OQP
= 180°- 40° – 40°
= 100°
Now, x° + ∠POQ + ∠QOR = 180° [a straight angle]
x° + 100° + 20° = 180°
x° = 180° – 120° = 60°
Hence, the value of x is 60.

(c) Here, Height of the tower (QR) = 50 m
Height of the tower (PT) = h m
Inrt. ∠ed ∆ PQR, ∠RPQ = 60°

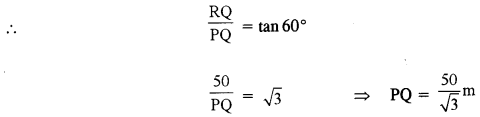
Also, inrt. ∠ed ∆ QPT, ∠TQP = 30°

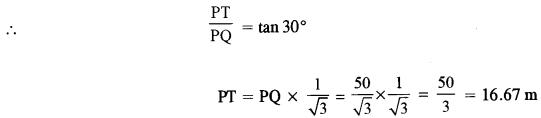
Hence, the required height of tower PT is 17 m (nearest to metre).

Question 11.
(a) The 4^th term of an A. P. is 22 and 15^th term is 66. Find the first term and the common difference. Hence find the sum of the series to 8 terms. [4]
(b) Use Graph paper for this question. [6]
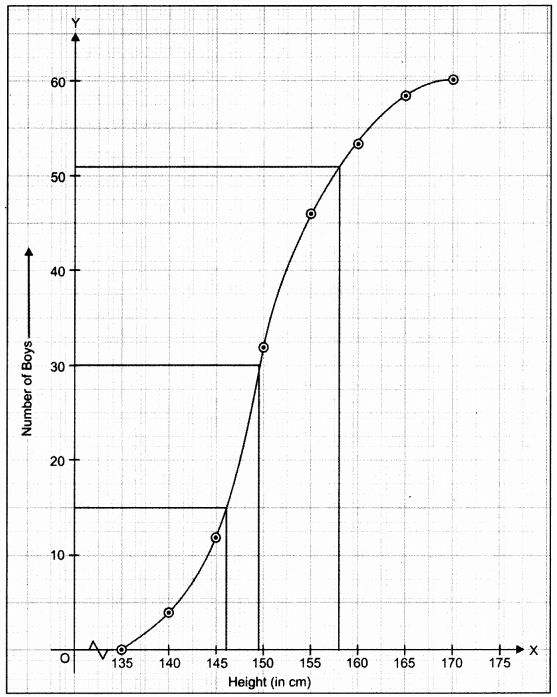
A survey regarding height (in cm) of 60 boys belonging to Class 10 of a school was conducted. The following data was recorded :

Taking 2 cm = height of 10 cm along one axis and 2 cm = 10 boys along the other axis draw and give of the above distribution. Use the graph to estimate the following:
(i) the median
(ii) lower Quartile
(iii) if above 158 cm is considered as the tall boys of the class. Find the number of boys in the class who are tall.
Answer.
(a) Let a and d be the first term and common difference of the required A.P.
∴ a₄ = 22
⇒ a + 3d = 22 ………(i)
And a₁₅ = 66
⇒ a + 14d = 66 ………..(ii)
Subtracting (i) from (ii), we have
(14d – 3d) = 66 – 22
11d = 44
d = 4
From (i), we have
a + 3(4) = 22
a = 22 – 12 = 10
Thus, a = 10 and d = 4
Now, S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
⇒ S₈= \(\frac{8}{2}\) [2(10) + (8-1)4]
S₈ = 4 [20 + 28]
S₈ = 4 x 48 S₈ = 192

(b) Given data was recorded as :

Plot the points (140,4), (145,12), (150,32), (155,46), (160,53), (165,59) and (170,60). Join them free hand to get the required ogive.
Now, from the graph, we obtain :

(i) Median height (in cm) = 149.5 cm
(ii) Lower Quartile = 146 cm ‘
(iii) Number of boys who are tall e., height above 158 cm = 60 – 51 = 9.


ICSE Class 10 Maths Previous Years Question Papers