ICSE Maths Question Paper 2017 Solved for Class 10

ICSE Maths Previous Year Question Paper 2017 Solved for Class 10

General Instructions :

• Answers to this Paper must be written on the paper provided separately.
• You will not be allowed to write during the first 15 minutes.
• This time is to be spent in reading the question paper.
• The time given at the head of this Paper is the time allowed for writing the answers.
• Attempt all questions from Section A and any four questions from Section B.
• All working, including rough work, must be clearly shown and must be done on the same sheet as the rest of the answer.
• Omission of essential working will result in the loss of marks.
• The intended marks for questions or parts of questions are given in brackets [ ].
• Mathematical tables are provided.
  

Section A [40 marks]
(Answer all questions from this Section)

Question 1.
(a) If b is the mean proportion between a and c, show that: [3]

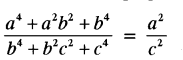
(b) Solve the equation 4x² – 5x – 3 = 0 and give your answer correct to two decimal places. [4]
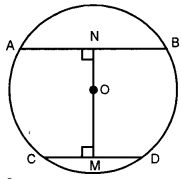
(c) AB and CD are two parallel chords of a circle such that AB = 24 cm and CD = 10 cm. If the radius of the circle is 13 cm, find the distance between the two chords. [3]

Solution :
(a) Here, b is the mean proportion between a and c.

∴ b² = ac

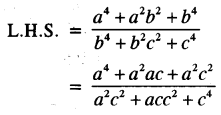
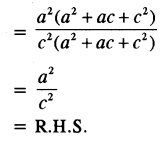
(b) Given equation is :
4x² – 5x – 3 =0
By using quadratic formula, we obtain

(c) Here, O is the centre of the given circle of radius 13 cm. AB and CD are two parallel chords, such that AB = 24 cm and CD = lo cm.
Join OA and OC.
Since ON⊥AB and 0M ⊥CD.
∴ M, O and N are collinear and M, N are mid-points of CD and AB.
Now, in rt. ∠ed ∆ANO, we have

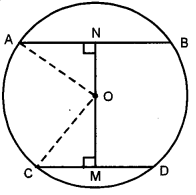
ON² = 02 AN²
= 13² – 12²
= 169 – 144 = 25
ON= \(\sqrt{25}\) = 5cm
Similarly, in it. ∠ed ∆CMO, we have
OM2 = OC² – CM²
= 13² – 5²
= 169 – 25 = 144
0M = \(\sqrt{144}\) = 12cm
Hence, distance between the two chords
NM = NO + OM
= 5 + 12
= 17 cm

Question 2.
(a) Evaluate without using trigonometric tables, [3]
sin²28° + sin²62° + tan²38° – cot²52° + sec²30°
(b) If A = \(\begin{bmatrix} 1 & 3 \\ 3 & 4 \end{bmatrix}\) and B = \(\begin{bmatrix} -2 & 1 \\ -3 & 2 \end{bmatrix}\) and A² – 5B² = 5C. Find matrix C where C is a 2 by 2 matrix. [4]
(c) Jaya borrowed ₹ 50000 for 2 years. The rates of interest for two successive years are 12% and 15% respectively. She repays ₹ 33000 at the end of the first year. Find the amount she must pay at the end of the second year to clear her debt. [3]
Solution :

(b) Here, A = \(\begin{bmatrix} 1 & 3 \\ 3 & 4 \end{bmatrix}\) and B = \(\begin{bmatrix} -2 & 1 \\ -3 & 2 \end{bmatrix}\)
Now, A2 = AA

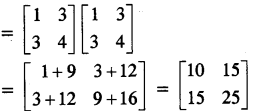
B2 = BB

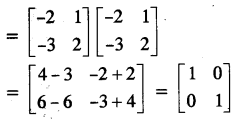
Again, 5C = A² – 5B²

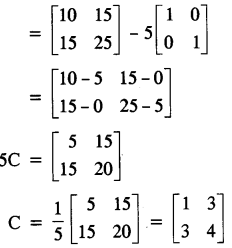
(c) Principal = ; 50000
Time =1 year
Rate = 12%

Question 3.
(a) The catalogue price of a computer set is 42000. The shopkeeper gives a discount of 10% on the listed price. He further gives an off-season discount of 5% on the discounted price. However, sales tax at 8% is charged on the remaining price after the two successive discounts. Find: [3]
(i) the amount of sales tax a customer has to pay.
(ii) the total price to be paid by the customer for the computer set.
(b) P(1, – 2) is a point on the line segment A(3, – 6) and B(x, y) such that AP : PB is equal to 2 : 3. Find the coordinates of B. [4]
(c) The marks of 10 students of a class in an examination arranged in ascending order is as follows : [3]
13, 35, 43, 46, x, x + 4, 55, 61, 71, 80
If the median marks is 48, find the value of x. Hence, find the mode of the given data
Solution :

Hence, amount of sales tax is ₹ 2872.80 and total price to be paid by the customer for the computer set is ₹ 38782.80.

(b) Here, AP : PB = 2 : 3, therefore, P divides AB in the ratio 2 : 3
Thus, coordinates of P are: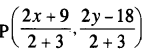

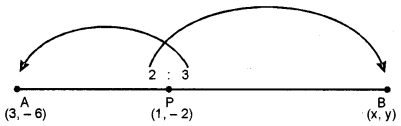
Also, coordinates of P are P(1, – 2)

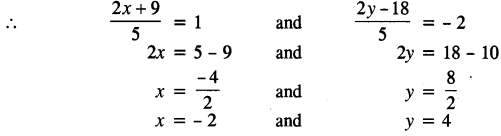
Hence, coordinates of B are B ( – 2, 4).

(c) Here, number of students are 10 i.e., even number of observations.

Thus, the observations are 13, 35, 43, 46, 46, 50, 55, 61, 71, 80.
Hence, the mode of the given data is 46.

Question 4.
(a) What must be subtracted from 16x³ – 8x² + 4x + 7 so that the resulting expression has 2x + 1 as a factor? [3]
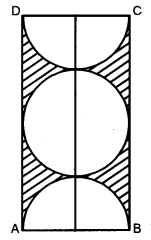
(b) In the given figure ABCD is a rectangle. It consists of a circle and two semi-circles each of which are of radius 5 cm. Find the area of the shaded region. Give your answer correct to three significant figures.

(c) Solve the following inequation and represent the solution set on a number line. [3]

Solution:
(a) Let p(x) = 16x³ – 8x² + 4x + 7 and g(x) = 2x + I
Put 2x + 1 = 0 ⇒ x = – \(\frac{1}{2}\)

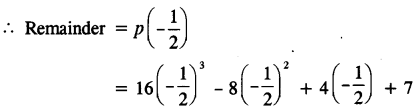
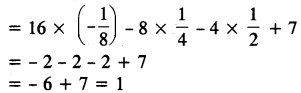
Hence, 1 is subtracted from p(x), so that g(x) is a factor of p(x).
(b) Here, radius of a circle and two semi-circles = 5 cm
Length of the rectangle = 5 + 10 + 5 = 20 cm
Breadth of the rectangle = 10 cm
Now, area of the shaded part = Area of rectangle – 2 × Area of circle

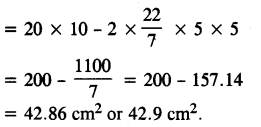
(c) Given inequation is :

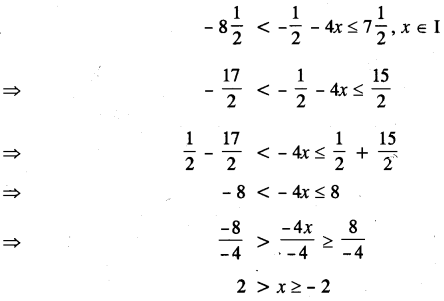
Solution set on number line

SECTION B [40 Marks]
Attempt any four questions from this Section

Question 5.
(a) Given matrix B = \(\begin{bmatrix} 1 & 1 \\ 8 & 3 \end{bmatrix}\) . Find the matrix X if, X=B2 – 4B. [4]
Hence, solve for a and b given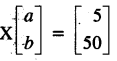
(b) How much should a man invest in 50 shares selling at 60 to obtain an income of 450, if the rate of dividend declared is 10%. Also, find his yield percent, to the nearest whole number. [3]
(c) Sixteen cards are labelled as a, b, c … m, n, o, p. They are put in a box and shuffled. A boy is asked to draw a card from the box. What is the probability that the card drawn is : [3]
(i) a vowel
(ii) a consonant
(iii) none of the letters of the word median? 
Solution :

Market value of a share = ₹ 60
Face value of a share = ₹ 50
Rate of dividend = 10%
Total income = ₹ 450
If income is 5, then investment = ₹ 60
If income is 1, then investment = \(\frac{60}{5}\) = ₹ 12
If income is 450, then investment = ₹ 12 × 450
= ₹ 54O0
Thus, total investment is ₹ 5480
∴ Yield percent = \(\frac{450}{5400}\) ×100
= 8.33
= 8 (to the nearest whole number)
(c) Total number of cards = 16
(i) Number of vowels = 4 (a, e, i, o)
Probability = \(\frac{4}{16}\) = \(\frac{1}{4}\)
(ii) Numberofeonsonant = 16 – 4 = 12
Probability = \(\frac{12}{16}\) = \(\frac{3}{4}\)
(iii) Probability (none of the letters of the word median) = \(\frac{10}{16}\) = \(\frac{5}{8}\)

Question 6.
(a) Using a ruler and a corrpass construct a triangle ABC in which AB = 7 cm, ∠CAB = 600 and AC = 5 cm. Construct the locus of : [4]
(i) points equidistant from AB and AC.
(ii) points equidistant from BA and BC.
Hence, construct a circle touching the three sides of the triangle internally.
(b) A conical tent is to accommodate 77 persons. Each person must have 16 n? of air to breathe. Given the radius of the tent as 7 m, find the height of the tent and also its curved surface area. [3]
(c) If \(\frac{7 m+2 n}{7 m-2 n}\) = \(\frac{5}{3}\) , use properties of proportion to find :
(i) m : n
(ii) \(\frac{m^{2}+n^{2}}{m^{2}-n^{2}}\)
Solution :
(a) Steps of Construction :

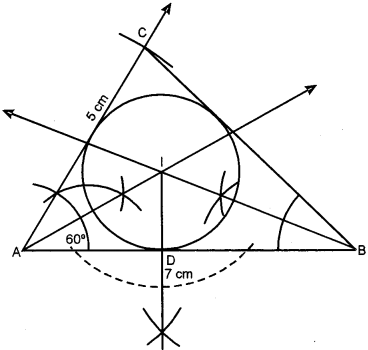
1. Draw a line segment AB = 7 cm.
2. At A construct an angle of 600 such that AC = 5 cm.
3. Join BC to get ∆ABC.
4. Draw angle bisector of ∠BAC, which is the required locus of the points equidistant from AB and AC.
5. Draw angle bisector of ∠ABC, which is the required locus of the points equidistant from BA and BC.
6. Let the two angle bisectors intersect each other in I.
7. Through I, draw ID⊥AB. With I as centre and radius = ID draw a circle which touches all the sides of the ∆ABC internally.
Total number of persons accommodated = 77
Volume of air required for each person = 16 m³
Volume of the conical tent = 77 × 16
= 1232 m3
Radius of the tent = 7 m
Let h be the height of the conical tent

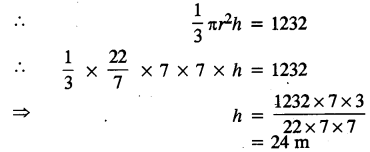
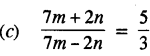
Using componendo and dividendo, we have

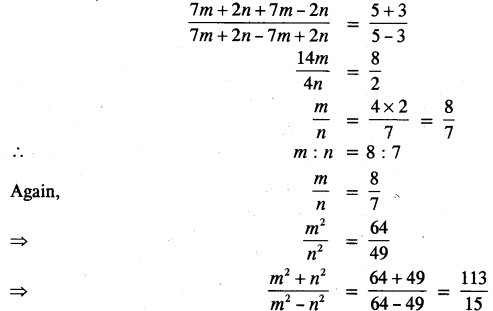
[Using componendo and dividendo]

Question 7.
(a) A page from a savings bank account passbook is given below: [5]

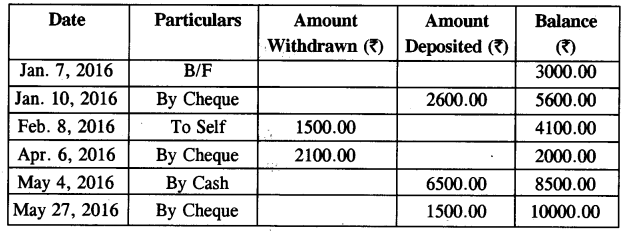
(i) Calculate the uterest for the 6 months from January to June 2016, at 6% per annum.
(ii) If the account is closed on 1st July 2016, find the amount received by the account holder.
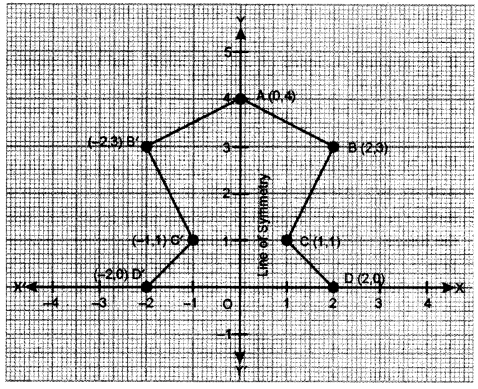
(b) Use a graph paper for this question (Take 2 cm =1 unit on both x and y axis) [5]
(i) Plot the following points:
A(0, 4), B(2, 3), C(1, 1) and D(2, 0).
(ii) Reflect points B, C, D on the y-axis and write down their coordinates. Name the images as B’, C’, D’ respectively.
(iii) Join the points A, B, C, D, D’, C’,B’ and A in order, so as to form a closed figure. Write down the equation of the line of symmetry of the figure formed.
Solution :
(a) Minimum balance for the month Jan., 2016 = ₹ 5600
Minimum balance for the month Feb., 2016 = ₹ 4100
Minimum balance for the month Mar., 2016 = ₹ 4100
Minimum balance for the month Apr., 2016 = ₹ 2000
Minimum balance for the month May, 2016 = ₹  8500
Minimum balance for the month June, 2016 = ₹ 10000
Total = ₹ 34300
Principal = ₹ 34300
Rate = 6% p.a.
Time = \(\frac{1}{12}\) year

(b) (E) On graph ,
(ii) B’(- 2, 3), C’(- 1, 1), D’(- 2, 0)
(iii) Equation of the line of symmetry is x = O

Question 8.
(a) Calculate the mean of the following distribution using step deviation method. [4]

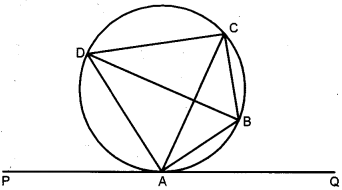
(b) In the given figure PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ = 30° prove that :
(i) BD is a diameter of the circle.
(ii) ABC is an isosceles triangle.

(C) The printed price of an air conditioner is ₹ 45000/-. The wholesaler allows a discount of 10% to the shopkeeper. The shopkeeper sells the article to the customer at a discount of 5% of the marked price. Sales tax (under VAT) is charged at the rate of 12% at every stage. Find :
(i) VAT paid by the shopkeeper to the government.
(ii) The total amount paid by the customer inclusive of tax. [3]
Solution :

Let assumed mean (a) = 35

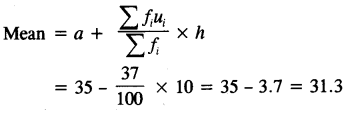
(b) Here PQ, is a tangent of the circle at A .

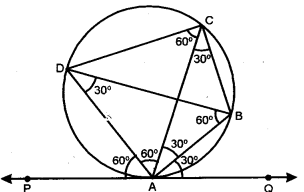
∠BAQ = 300. Since AB is
angle bisector of ∠CAQ.
∴ ∠CAB = ∠BAQ = 300
Again, ∠PAC = 180° – ∠CAQ
= 180°- 30°- 30°
= 120°
Also, AD is angle bisector of ∠PAC
∴ ∠PAD = ∠CAD = 600
Since angles in the corresponding alternate segment are equal
∴ ∠ADB =∠BAQ = 300 and ∠DBA = ∠PAD = 60°
Also, angles in same segment are equal
∴ ∠DCA = ∠DBA = 600
and ∠ACB = ∠ADB = 30°
Now, ∠DCB = ∠DCA + ∠ACB = 600 + 300 = 90°
We know that angle in a semi-circle is right angle.
Thus, BD is a diameter of the circle.
In ∆ACB, ∠ACB = ∠CAB = 30°
Hence, ∆ABC is an isosceles triangle.
List price of air conditioner = 45000
Discount = 10%
Thus, VAT paid by the shopkeeper to the government = ₹ (5130 – 4860) = ₹ 270
Total amount paid by the customer = ₹ (42750 + 5130) = ₹ 47880

Question 9.
(a) In the figure given, O is the centre of the circle. LDAE = 700.
Find giving suitable reasons, the measure of: [4]
(i) ∠BCD
(ii) ∠BOD
(iii) ∠OBD

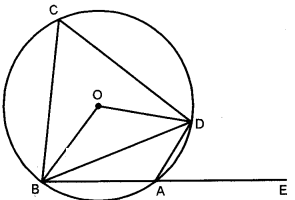
(b) A(-1, 3), B(4, 2) and C(3, -2) are the vertices of a triangle. [3]
(i) Find the coordinates of the centroid G of the triangle.
(ii) Find the equation of the line through G and parallel to AC.
(c) Prove that: [3]

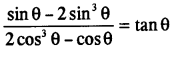
Solution :
(a) Here, ∠DAE = 70°
∴ ∠BAD = 180° ∠DAE
[a linear pair]
= 180° – 70° = 110°
ABCD is a cyclic quadrilateral
∴ ∠BCD + ∠BAD = 180°
∠BCD + 110° = 180°
⇒ ∠BCD = 180° – 110°
= 70°

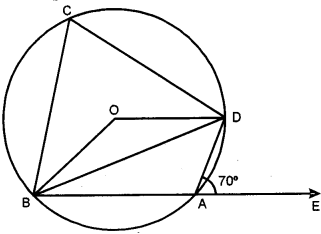
Since angle subtended by an arc at the centre of a circle is twice the angle subtended at the remaining part of the circle.
∴ ∠BOD = 2∠BCD = 2 × 70° = 140°
In ∆OBD, OB = OD = radii of same circle.
∴ ∠OBD =∠ODB
Thus, ∠OBD = \(\frac{1}{2}\) (180° – ∠BOD) = \(\frac{1}{2}\) (180° – 140°) = \(\frac{1}{2}\) × 40° = 20°
(b) A(-1, 3), B(4, 2) and C(3, -2) are the vertices of ∆ABC.
∴ Coordinates of the centroid G of the ∆ABC are :

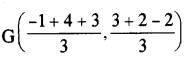
G(2, 1)
Here, line ‘l’ is drawn through G(2, 1) and parallel to the line AC.
∴ Slope of the line l = Slope of the line AC

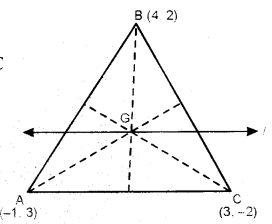
\(\frac{-2-3}{3+1}\) = \(\frac{-5}{4}\)
y – 1 = \((\begin{matrix} -5 \\ 4 \end{matrix}\)) (x – 2)
4y – 4 = – 5x + 10
5x + 4y = 14

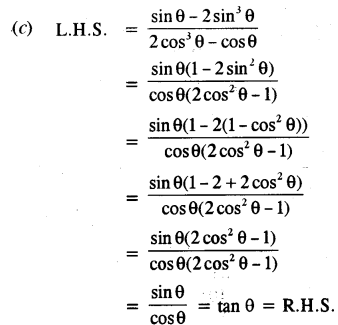
Question 10. .
(a) The sum of the ages of Vivek and his younger brother Amit is 47 years. The product of their ages in years is 550. Find their ages. [4]
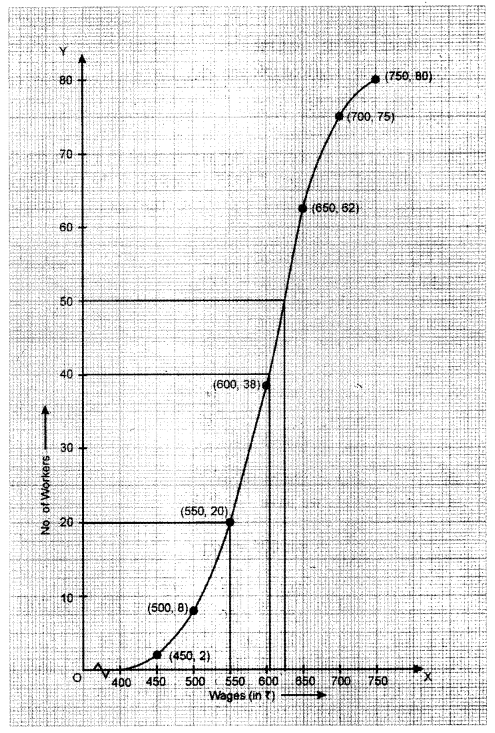
(b) The daily wages of 80 workers in a project are given below

Use a graph paper to draw an ogive for the above distribution. (Use a scale of 2 cm = ₹ 50 on x-axis and 2 cm = 10 workers on y-axis. Use your ogive to estimate:
(i) the median wage of the workers.
(ii) the lower quartile wage of workers.
(iii) the number of workers who earn more than ₹ 625 daily.
Solution:
(a) Let Vivek’s age be x years
∴ Amit’s age = 47 – x
Also, product of their ages = 550
∴ x(47 – x) = 550
47x – x² = 550
⇒ x² – 47x + 550 =0
⇒ x² – 25x – 22x + 550 = 0
⇒ x(x – 25) – 22(x – 25) = 0
⇒ (x – 25)(x – 22)= 0
⇒ x = 25
or x = 22
Since Vivek is elder brother of Amit.
Hence, age of Vivek is 25 years and age of Amit is 22 years.
(b) The cumulative frequency distribution for the given data is :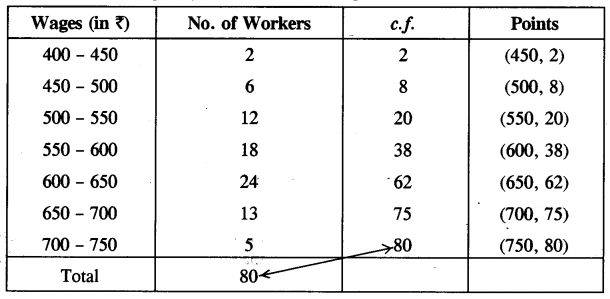
Plot the points (450, 2), (500, 8), (550, 20), (600, 38), (650, 62), (700, 75), (750, 80).
Join them free hand to get the required ogive.
Now, from the graph, we obtain:
(i) median wage of the workers = ₹ 605
(ii) lower quartile wage of workers = ₹ 550
(iii) Number of workers who earn more than ₹ 625 daily = 80 – 50 = 30.

Question 11.
(a) The angles of depression of two ships A and B as observed from the top of a light house 60 m high are 60° and 45° respectively. If the two ships are on the opposite sides of the light house, find the distance between the two ships. Give your answer correct to the nearest whole number. [4]
(b) PQR is a triangle. S is a point on the side QR of ∆PQR such that
∠PSR = ∠QPR.
Given QP = 8 cm, PR = 6 cm and SR = 3 cm. [3]

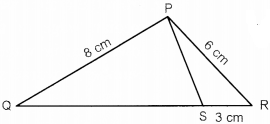
(i) Prove ∆PQR ~ ∆SPR
(ii) Find the length of QR and PS
(iii) \(\frac{\text { area of } \Delta \mathrm{PQR}}{\text { area of } \Delta \mathrm{SPR}}\)
(c) Mr. Richard has a recurring deposit account in a bank for 3 years at 7.5% p.a. simple interest. If he gets ₹ 8325 as interest at the time of maturity, find : [3]
(i) The monthly deposit
(ii) The maturity value.
Solution:
(a) Let PQ be the light house of height 60m, A and B are the two ships on the opposite sides of the light house, such that:
∠PAQ = 60°, ∠PBQ
= 45°
In rt ∠ed ∆PQB, we have

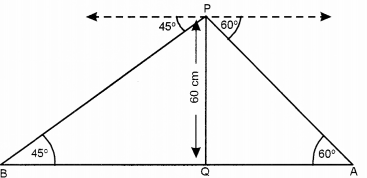
\(\frac{\mathrm{PQ}}{\mathrm{QB}}\) = tan 45° = 1
⇒ PQ =QB = 60 m
In rt ∠ed ∆PQA, we have

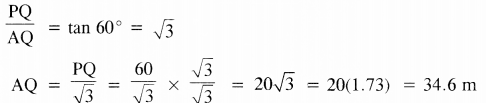
Now, AB = AQ + QB = 60 + 34.6 = 94.6m
Hence, the distance between the two ships is 95 m (nearest to whole number).

(b) Given : QP = 8 cm, PR = 6 cm and SR = 3 cm
In ∆PQR and ∆SPR
∠QPR = ∠PSR (given)
∠QRP = ∠SRP (common)
∴ ∆PQR ~ ∆SPR (by AA similarity rule)
Since ∆PQR ~ ∆SPR

(c) Let the monthly deposit be ₹ x
Time = 3 years or 36 months, R = 7.5%, Interest = ₹ 8325.

Thus, the monthly deposit is ₹ 2000
The maturity value = ₹ 36 × 2000 + ₹ 8325
= ₹ 72000 + ₹ 8325 = ₹ 80325.

ICSE Class 10 Maths Previous Years Question Papers