What is a Function?

Definition of function

Function can be easily defined with the help of the concept of mapping. Let X and Y be any two non-empty sets. “A function from X to Y is a rule or correspondence that assigns to each element of set X, one and only one element of set Y”. Let the correspondence be ‘f’ then mathematically we write f : X ⟶ Y where y = f(x), x ∈ X and y ∈ Y. We say that ‘y’ is the image of ‘x’ under f (or x is the pre image of y).
Two things should always be kept in mind:

A mapping f : X ⟶ Y is said to be a function if each element in the set X has its image in set Y. It is also possible that there are few elements in set Y which are not the images of any element in set X.
Every element in set X should have one and only one image. That means it is impossible to have more than one image for a specific element in set X. Functions can not be multi-valued (A mapping that is multi-valued is called a relation from X and Y) e.g.

Testing for a function by vertical line test

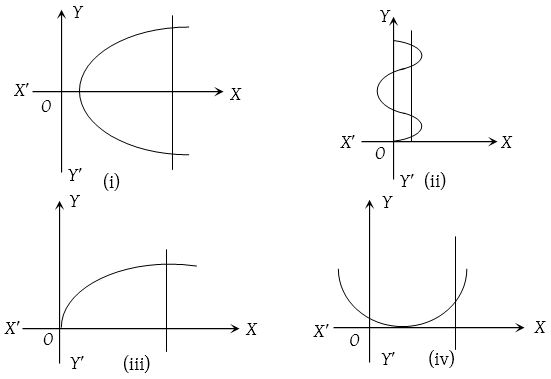
A relation f : A ⟶ B is a function or not it can be checked by a graph of the relation. If it is possible to draw a vertical line which cuts the given curve at more than one point then the given relation is not a function and when this vertical line means line parallel to Y-axis cuts the curve at only one point then it is a function. Figure (iii) and (iv) represents a function.
What is a Function 2

Number of functions

Let X and Y be two finite sets having m and n elements respectively. Then each element of set X can be associated to any one of n elements of set Y. So, total number of functions from set X to set Y is n^m.

Value of the function

If y = f(x) is a function then to find its values at some value of x, say x = a we directly substitute x = a in its given rule f(x) and it is denoted by f(a).
e.g. If f(x) = x² + 1, then f(1) = 1² + 1 = 2, f(2) = 2² + 1 = 5, f(0) = 0² + 1 = 1, etc.

Algebra of functions

Scalar multiplication of a function:
(c f)x = c f(x) where c is a scalar. The new function has the domain X_f.
Addition/subtraction of functions:
(f ± g)(x) = f(x) ± g(x). The new function has the domain X.
Multiplication of functions:
(f.g)(x) = (g.f)(x) = f(x)g(x). The product function has the domain X.
Division of functions:
(i) \(\left( \frac { f }{ g } \right) (x)=\frac { f(x) }{ g(x) }\). The new function has the domain X, except for the values of x for which g(x) = 0.
(ii) \(\left( \frac { g }{ f } \right) (x)=\frac { g(x) }{ f(x) }\). The new function has the domain X, except for the values of x for which f(x) = 0.
Equal functions: Two function f and g are said to be equal functions, if and only if
(i) Domain of f = Domain of g.
(ii) Co-domain of f = Co-domain of g.
(iii) f(x) = g(x) ∀ x ∈ their common domain.
Real valued function: If R, be the set of real numbers and A, B are subsets of R, then the function f : A ⟶ B is called a real function or real –valued function.