FACTORS AND MULTIPLES
Mr Sharma wanted to withdraw Rs. 1000 from his bank account to purchase books for his children. The cashier gave him 10 hundred-rupee notes, i.e.,
Rs. 10 × 100 = Rs. 1000
Mr Sharma got the required amount. But the cashier could also give the same amount in the following ways:

Here, we observe that in each case Mr Sharma got the same amount of Rs. 1000. These numbers 1, 2, 5, 10, 20, 50, 100, 200, 500, and 1000 are factors of 1000. Hence, 1000 is a multiple of these numbers.
Here we will discuss only the natural numbers, that is positive integers.
If a = b × c, we say b and c are factors of a and a is a multiple of c and b.
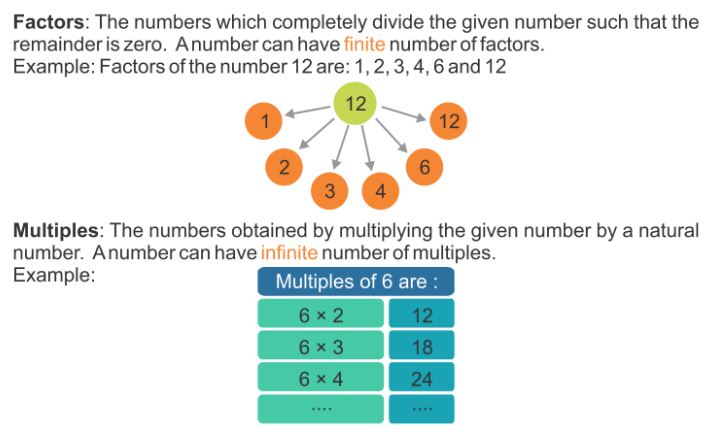
Factors
Factor: A number which divides a given number exactly (without leaving any remainder) is called a factor of the given number.
Example: Factors of 12
12 = 1 × 12
12 = 2 × 6
12 = 3 × 4
Here, 1, 2, 3, 4, 6, and 12 are factors of 12.

Properties of Factors
- Every non-zero number is a factor of itself.
Examples: 5 is a factor of 5. (5 ÷ 5 = 1)
12 is a factor of 12. (12 ÷ 12 = 1) - 1 is a factor of every number.
Examples: 1 is a factor of 5. (5 ÷ 1 = 5)
1 is a factor of 12. (12 ÷ 1 = 12) - Every non-zero number is a factor of 0.
Example: 5 and 12 are factors of 0 because
0 ÷ 5 = 0 and 0 ÷ 12 = 0 - The factors of a number are finite.
Multiples
Multiple: A multiple of any natural number is a number formed by multiplying it by another natural number.
Example: Multiples of 6 are 6 × 1 = 6; 6 × 2 = 12; 6 × 3 = 18; 6 × 4 = 24
Here, 6,12,18,24 are multiples of 6.
Example: Let us find the LCM and HCF of 24 and 36.
Factors of 24 = 1, 2, 3, 4, 6, 8, 12, 24
Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18, 36
Here, the highest common factor is 12.
∴ HCF = 12
Multiples of 24 = 24, 48, 72, 96,…
Multiples of 36 = 36, 72, 108,…
Here, the lowest common multiple is 72.
∴ LCM = 72

Properties of Multiples
- Every number is a multiple of itself.
Examples
(a) 3 × 1 = 3; 3 is the multiple of 3
(b) 7 × 1 = 7; 7 is the multiple of 7 - Every number is the multiple of 1.
Examples
(a) 1 × 3 = 3; 3 is the multiple of 1
(b) 1 × 7 = 7; 7 is the multiple of 1 - The multiples of a number are infinite (unlimited).
Even numbers: A number which is a multiple of 2 is called an even number.
Example: 2, 4, 6, 8, 10,…
Odd numbers: A number which is not a multiple of 2 is called an odd number.
Example: 1, 3, 5, 7, 9, 11,…
Prime numbers: A number which is greater than 1, and has exactly two factors (1 and the number itself) is called a prime number.
Example: Factors of 2 = 1, 2
Factors of 3 = 1, 3
Factors of 5 = 1, 5
Factors of 7 = 1, 7
Factors of 11 = 1, 11
Here, 2, 3, 5, 7, 11 etc. are all prime numbers.
Composite numbers: A number, which is greater than 1 and has more than two factors is called a composite number.
Examples: Here,
Factors of 4 = 1, 2, 4
Factors of 6 = 1, 2, 3, 6
Factors of 8 = 1, 2, 4, 8
Factors of 9 = 1, 3, 9
Factors of 10 = 1, 2, 5
FINDING PRIME NUMBERS FROM 1 TO 100
We can find the prime numbers from 1 to 100 by following these steps (given by the Greek mathematician Eratosthenes).
Step 1: Prepare a list of numbers from 1 to 100.
Step 2: As 1 is neither prime nor composite number, cross it out.
Step 3: Encircle ‘2’ as a prime number and cross out all its other multiples.
Step 4: Encircle ‘3’ as a prime number and cross out all its other multiples.
Step 5: Encircle ‘5’ as a prime number and cross out all its other multiples.
Step 6: Continue this process till all the numbers are either encircled or crossed out.
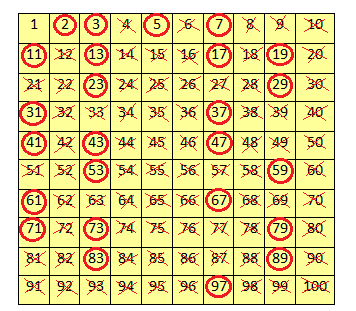
All the encircled numbers are prime numbers and the crossed out numbers (except 1) are composite numbers.
Numbers 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 are the prime numbers between 1 and 100.
This is called the ‘Sieve of Eratosthenes’.
Twin primes: Two prime numbers having a difference of 2 are known as twin primes.
Example: ( 3, 5 ), ( 5,7 ), (11,13 ), (17,19 ), etc are twin primes.
Co-primes: Two numbers are said to be co-primes if they have no common factor other than 1. In other words, two natural numbers are co-primes if their HCF is 1.
Example: ( 2, 3 ), ( 3, 4 ), ( 5, 6 ), ( 7, 8 ), and so on.
Example 1: Is 16380 a multiple of 28?
Solution: To check whether 16380 is a multiple of 28 or not, we have to divide 16380 by 28. If the remainder becomes zero, then it is a multiple of the number.
So, 16380 = 28 × 585, hence 16380 is a multiple of 28.
Example 2: Express 29 as the sum of three odd prime numbers.
Solution: 29 = 19 + 7 + 3
All 19, 7, and 3 are odd prime numbers.
DIVISIBILITY TESTS FOR 2, 3, 4, 5, 6, 7, 8, 9, 10, AND 11
If we want to know that a number is divisible by another number, we generally perform the actual division and see whether the remainder is zero or not. This process is time-consuming for division of large numbers. Therefore, to cut short our efforts, some divisibility tests of different numbers are given below.
Test of Divisibility by | Condition | Example |
2 | A number is divisible by 2, if its ones digit is 0, 2, 4, 6 or 8. | 1372, 468, 500, 966 are divisible by 2, since their ones digit is 2, 8, 0 and 6 respectively. |
3 | A number is divisible by 3, if the sum of its digits is divisible by 3. | In 1881, the sum of digits is 1 + 8 + 8 + 1 = 18 which is divisible by 3. So 1881 is divisible by 3. |
4 | A number is divisible by 4, if the number formed by the last two digits is divisible by 4. | 30776, 63784, 864 are all divisible by 4. Since last two digits of the numbers, i.e., 76, 84, and 64 are divisible by 4. |
5 | A number is divisible by 5, if its ones digit is either 5 or 0. | 675, 4320, 145 all are divisible by 5 because their ones digit is 5 or 0. |
6 | A number is divisible by 6, if the number is divisible by 2 and 3. | In 5922, ones digit is 2, so it is divisible by 2. The sum of digits in 5922 is 5 + 9 + 2 + 2 = 18, which is divisible by 3. So, 5922 is divisible by 6. |
7 | A number is divisible by 7, if the difference between twice the last digit and the number formed by other digits is either 0 or a multiple of 7. | In number 2975, it is observed that the last digit in 2975 is 5. So, 297 – (2 x 5) = 287, which is a multiple of 7. Hence, 2975 is divisible by 7. |
8 | A number is divisible by 8, if the number formed by its last three digits is divisible by 8. | In 213456, the last three digits are 456 which is divisible by 8. So, the number 213456 is divisible by 8. |
9 | A number is divisible by 9, if the sum of its digits is divisible by 9. | In 538425, the sum of the digits are (5 + 3 + 8 + 4 + 2 + 5) = 27 which is divisible by 9. So, 538425 is divisible by 9. |
10 | A number is divisible by 10, if the digit at ones place of the number is 0. | The numbers 980, 63990 are all divisible by 10 because their ones digit is 0. |
11
| A number is divisible by 11, if the difference between the sum of digits at odd places and the sum of digits at even places is either 0 or a multiple of 11. | In number 27896, the sum of the digits at odd places are (2 + 8 + 6) = 16. The sum of the digits at even places are (7 + 9 ) = 16. Their difference is 16 – 16 = 0. So, the number 27896 is divisible by 11. |
Example 3: Test whether 72148 is divisible by 8 or not?
Solution: Here, the number formed by the last three digits is 148, which is not divisible by 8.
So, 72148 is not divisible by 8.
Example 4: Test whether 8050314052 is divisible by 11 or not?
Solution: The sum of the digits at even places = 8 + 5 + 3 + 4 + 5 = 25
The sum of digits at the odd places = 0 + 0 + 1 + 0 + 2 = 3
Difference = 25 – 3 = 22 22 is divisible by 11.
So, the number 8050314052 is divisible by 11.