Finding Domains of Composite Functions
At times, the domain of a composite function can be a bit confusing. Let’s examine what happens to values as they “travel” through a composition of functions.

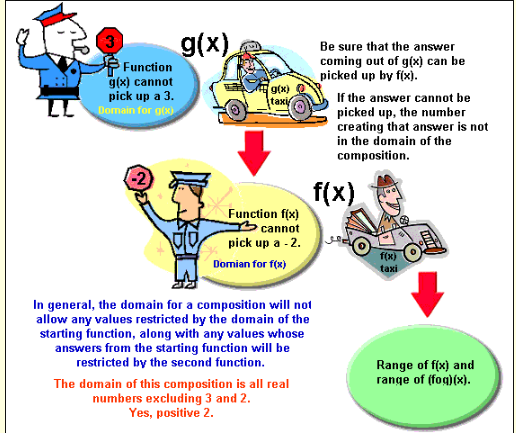
In this problem, function cannot pick up the value x = 3, and function cannot pick up the value x = -2.
The domain of will be the values from the domain of g(x) which can “move through” to the end of the composition. This means that
the answers created by these values from function must be “picked up” by function f(x).
Let’s follow this process algebraically:
1. Function cannot pick up the value 3. Consequently, the composition also cannot pick up the value 3.
2. The answers coming out of function come out in the form x/x-3. Since function f(x) cannot pick up -2, we must lookout for any values of x that cause
x/x-3 =-2 since these values create an answer that cannot progress through the composition (cannot be picked up by function f(x) ).
3. When does x-x-3= -2 ? Solve algebraically ….
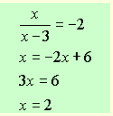
4. The domain of will be all real numbers with the exclusion of 3 and 2.
(Notice that one of the excluded values is 2, not -2. The value x = -2 makes it through the composition very nicely because its answer from function g(x) is 2/5 which is then picked up by function f(x) )
Is there an easier way to find the domain of a composition?
If you are finding the algebraic expression for the composition of two functions, you can examine your answer to determine any additional restrictions on the domain of the composition. Let’s continue with our problem….
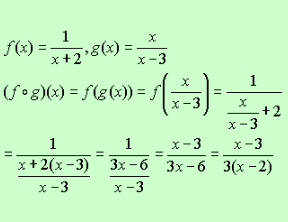
The algebraic expression for this composition (the final answer)”SHOWS” us that x = 2 would not be an acceptable domain element since it creates a zero denominator problem in the answer.
Just remember that you must also specify any restrictions on the domain of the starting function. In this problem, x = 3 is not allowed since it is a restriction on g(x).
Answer: The domain of the composition is all real numbers with the exclusion of 3 and 2.