Even and Odd Functions

Even and Odd Functions

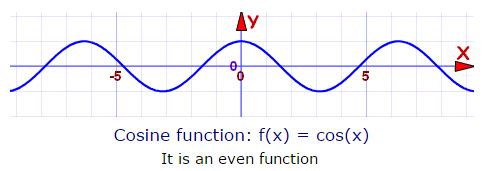
(1) Even function: If we put (–x) in place of x in the given function and if f(–x) = f(x), ∀ x ∈ domain then function f(x) is called even function. e.g. f(x) = e^x + e^-x , f(x) = x², f(x) = x sin x, f(x) = cos x, f(x) = x² cos x all are even functions.

Examples: 

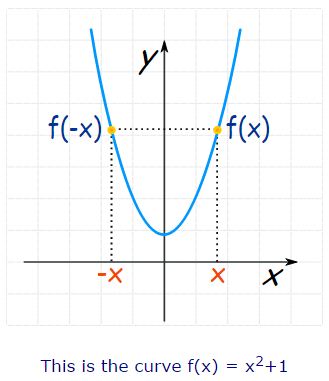
1. f(x) = x² + 1
   
2. f(x) = cos x
   

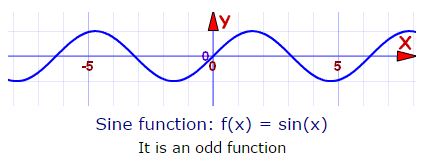
(2) Odd function: If we put (–x) in place of x in the given function and if f(–x) = –f(x), ∀ x ∈ domain then f(x) is called odd function. e.g. f(x) = e^x – e^-x , f(x) = x³, f(x) = sin x, f(x) = x cos x, f(x) = x² sin x all are odd functions.

Examples: 

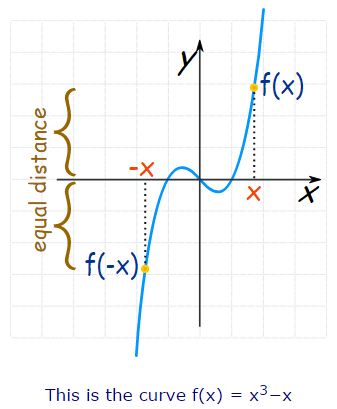
1. f(x) = x³ – x
   
2. f(x) = sin x
   

Properties of even and odd function

• The graph of even function is always symmetric with respect to y-axis. The graph of odd function is always symmetric with respect to origin.
• The product of two even functions is an even function.
• The sum and difference of two even functions is an even function.
• The sum and difference of two odd functions is an odd function.
• The product of two odd functions is an even function.
• The product of an even and an odd function is an odd function. It is not essential that every function is even or odd. It is possible to have some functions which are neither even nor odd function. e.g. f(x) =  x²+ x³, f(x) = log_e x, f(x) = e^x.
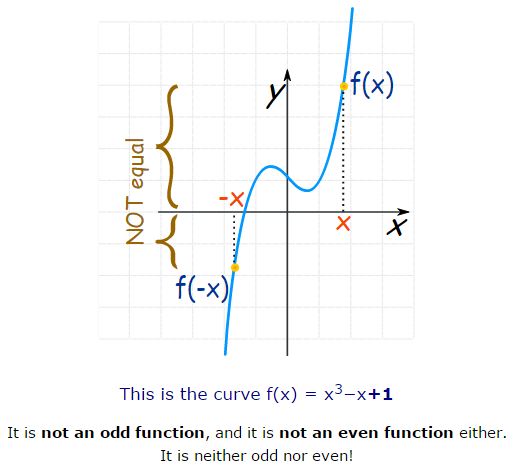
• The sum of even and odd function is neither even nor odd function.
• Zero function f(x) = 0 is the only function which is even and odd both.

Periodic function

A function is said to be periodic function if its each value is repeated after a definite interval. So a function f(x) will be periodic if a positive real number T exist such that, f(x + T) = f(x), ∀ x ∈ domain. Here the least positive value of T is called the period of the function.

Clearly f(x) = f(x + T) = f(x + 2T) = f(x + 3T) = …… e.g., sin x, cos x, tan x are periodic functions with period 2π, 2π and π respectively.

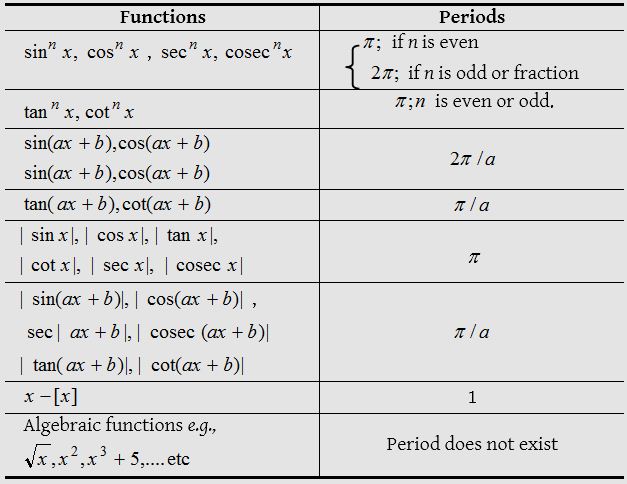
Some standard results on periodic functions

Composite function

If f : A ⟶ B and g : B ⟶ C are two function then the composite function of f and g, gof A ⟶ C will be defined as gof(x) = g[f(x)], ∀ x ∈ A.

Properties of composition of function:

1. f is even, g is even ⇒ fog is even function.
2. f is odd, g is odd ⇒ fog is odd function.
3. f is even, g is odd ⇒ fog is even function.
4. f is odd, g is even ⇒ fog is even function.
5. Composite of functions is not commutative i.e., fog ≠ gof.
6. Composite of functions is associative i.e., (fog)oh = fo(goh)
7. If f : A ⟶ B is bijection and g : B ⟶ A is inverse of f. Then fog = I_B and gof = I_A where, I_A and I_B are identity functions on the sets A and B respectively.
8. If f : A ⟶ B and g : B ⟶ C are two bijections, then gof A ⟶ C is bijection and (gof)^-1 = (f^-1og^-1).
9. fog ≠ gof but if, fog = gof then either f^-1 = g or g^-1 = f also, (fog)(x) = (gof)(x) = (x).
10. gof(x) is simply the g-image of f(x), where f(x) is f-image of elements x ∈ A.
11. Function gof will exist only when range of f is the subset of domain of g.
12. fog does not exist if range of g is not a subset of domain of f.
13. fog and gof may not be always defined.
14. If both f and g are one-one, then fog and gof are also one-one.
15. If both f and g are onto, then gof is onto.