Definition of Inverse Function
If f : A ⟶ B be a one-one onto (bijection) function, then the mapping f-1 : B ⟶ A which associates each element a ∈ A with element such that f(a) = b is called the inverse function of the function f : A ⟶ B.
f-1 : B ⟶ A, f-1(b) = a ⇒ f(a) = b
In terms of ordered pairs inverse function is defined as f-1(b, a) if (a, b) ∈ f.
For the existence of inverse function, it should be one-one and onto.
Properties of Inverse function:
- Inverse of a bijection is also a bijection function.
- Inverse of a bijection is unique.
- (f–1)–1= f
- If f and g are two bijections such that (gof) exists then (gof)–1 = f–1og–1.
- If f : A ⟶ B is a bijection then f–1. B ⟶ A is an inverse function of f. f–1of = IA and fof–1 = IB. Here IA, is an identity function on set A, and IB, is an identity function on set B.

A function and its inverse function can be described as the “DO” and the “UNDO” functions. A function takes a starting value, performs some operation on this value, and creates an output answer. The inverse function takes the output answer, performs some operation on it, and arrives back at the original function’s starting value.
This “DO” and “UNDO” process can be stated as a composition of functions. If functions f and g are inverse functions, f(g(x)) = g(f(x)) . A function composed with its inverse function yields the original starting value. Think of them as “undoing” one another and leaving you right where you started.
So how do we find the inverse of a function?
Basically speaking, the process of finding an inverse is simply the swapping of the x and y coordinates. This newly formed inverse will be a relation, but may not necessarily be a function.
Consider this subtle difference in terminology:
Definition: INVERSE OF A FUNCTION: The relation formed when the independent variable is exchanged with the dependent variable in a given relation. (This inverse may NOT be a function.)
Definition: INVERSE FUNCTION: If the above mentioned inverse of a function is itself a function, it is then called an inverse function.
Remember:
The inverse of a function may not always be a function!
The original function must be a one-to-one function to guarantee that its inverse will also be a function.
Definition: A function is a one-to-one function if and only if each second element corresponds to one and only one first element. (each x and y value is used only once)
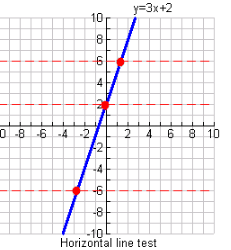
Use the horizontal line test to determine if a function is a one-to-one function.
If ANY horizontal line intersects your original function in ONLY ONE location, your function will be a one-to-one function and its inverse will also be a function.
The function y = 3x + 2, shown at the right, IS a one-to-one function and its inverse will also be a function.
(Remember that the vertical line test is used to show that a relation is a function.)
Definition: The inverse of a function is the set of ordered pairs obtained by interchanging the first and second elements of each pair in the original function.
Should the inverse of function f (x) also be a function, this inverse function is denoted by f-1 (x).
Note: If the original function is a one-to-one function, the inverse will be a function.
[The notation f-1 (x) refers to “inverse function”. It does not algebraically mean 1/f (x).]
Swap ordered pairs: If your function is defined as a list of ordered pairs, simply swap the x and y values. Remember, the inverse relation will be a function only if the original function is one-to-one.
Examples:

Solve algebraically: Solving for an inverse relation algebraically is a three step process:
1. Set the function = y
2. Swap the x and y variables
3. Solve for y
Examples:

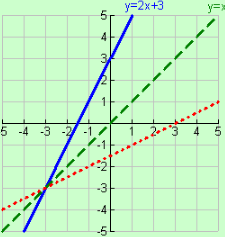
Graph: The graph of an inverse relation is the reflection of the original graph over the identity line,
y = x. It may be necessary to restrict the domain on certain functions to guarantee that the inverse relation is also a function. (Read more about graphing inverses.)
Example:
Consider the straight line, y = 2x + 3, as the original function. It is drawn in blue.
If reflected over the identity line, y = x, the original function becomes the red dotted graph. The new red graph is also a straight line and passes the vertical line test for functions. The inverse relation of y = 2x + 3 is also a function.
Not all graphs produce an inverse relation which is also a function.