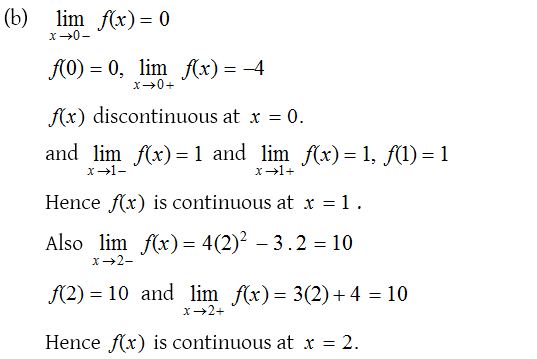Continuous Function
Continuity
The word ‘continuous’ means without any break or gap. If the graph of a function has no break or gap or jump, then it is said to be continuous.
A function which is not continuous is called a discontinuous function. While studying graphs of functions, we see that graphs of functions sin x, x, cos x, ex etc. are continuous but greatest integer function [x] has break at every integral point, so it is not continuous. Similarly tan x, cot x, sec x, 1/x etc. are also discontinuous function.

Continuity of a function at a point
A function f(x) is said to be continuous at a point x = a of its domain if and only if it satisfies the following three conditions :

Cauchy’s definition of continuity:
A function f is said to be continuous at a point a of its domain D if for every ε > 0 there exists δ > 0 (dependent on ε) such that |x − a| < δ ⇒ |f(x) – f(a)| < ε.
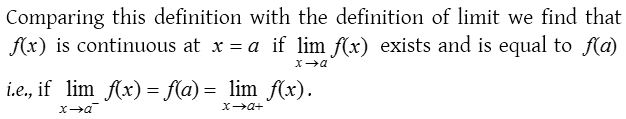
Continuity from left and right
Function f(x) is said to be
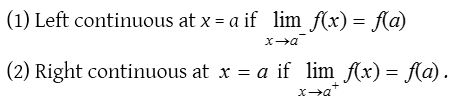
Thus a function f(x) is continuous at a point x = a if it is left continuous as well as right continuous at x = a.
Properties of continuous functions
Let f(x) and g(x) be two continuous functions at x = a Then
- A function f(x) is said to be everywhere continuous if it is continuous on the entire real line R i.e.(-∞, ∞). e.g., polynomial function, ex, sin x, x, cos x, constant, xn, |x − a| etc.
- Integral function of a continuous function is a continuous function.
- If g(x) is continuous at x = a and f(x) is continuous at x = g(a) then (fog) (x) is continuous at x = a.
- If f(x) is continuous in a closed interval [a,b] then it is bounded on this interval.
- If f(x) is a continuous function defined on [a, b] such that f(a) and f(b) are of opposite signs, then there is atleast one value of x for which f(x) vanishes. i.e. if f(a) > 0, f(b) < 0 ⇒ ∃c ∈ (a, b) such that f(c) = 0.
Discontinuous function
Discontinuous function: A function ‘f’ which is not continuous at a point in its domain is said to be discontinuous there at x = a. The point ‘a’ is called a point of discontinuity of the function.
The discontinuity may arise due to any of the following situations.
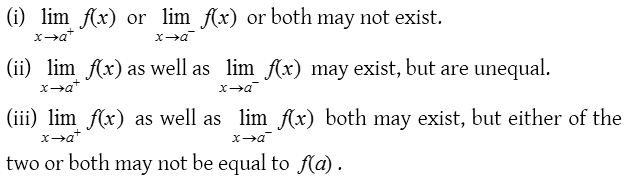
Continuous Function Problems with Solutions
1.

Solution:
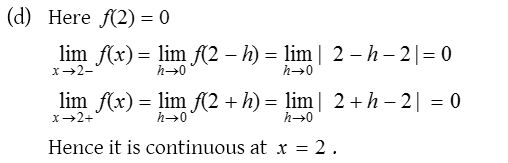
2.
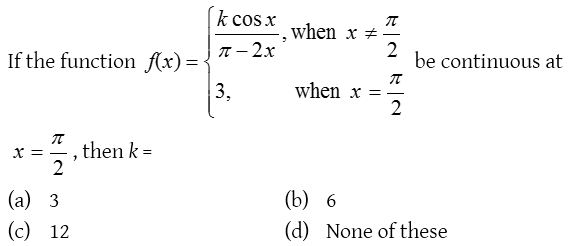
Solution:
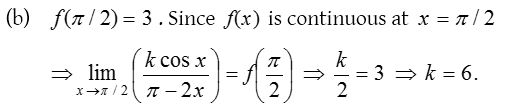
3.
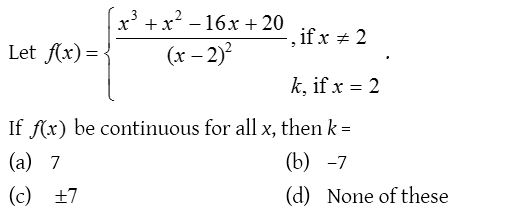
Solution:
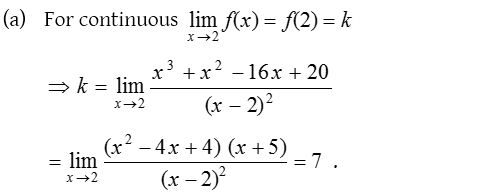
4.
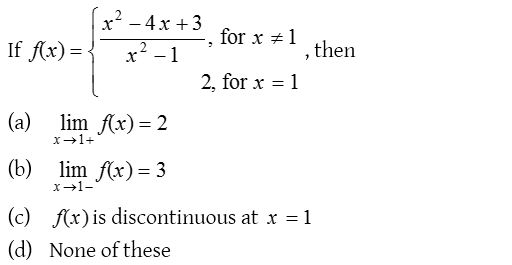
Solution:
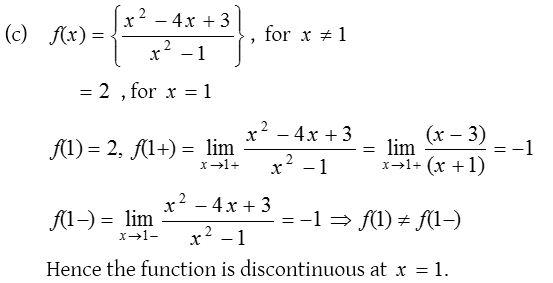
5.

Solution: