How To Construct A Tangent To A Circle From An External Point

Steps of construction
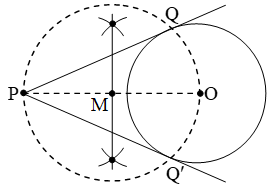 1. Take given circle and a point P outside the circle. O is centre of the circle.
1. Take given circle and a point P outside the circle. O is centre of the circle.
2. Joint OP.
3. Bisect OP and get its mid-point M.
4. Draw circle with centre M and radius = PM = MO.
5. Circle drawn meets the given circle at Q above PO and at Q’ below PO.
6. Join PQ and PQ’.
7. PQ and PQ’ are the required tangents drawn to the circle from the point P.
We observe that PQ = PQ’.
Read More:
Construction Of Tangent To A Circle From An External Point
Example 1: Draw a circle of radius 3 cm. Take a point at a distance of 5.5 cm from the centre of the circle. From point P, draw two tangents to the circle.
Sol. Steps of Construction
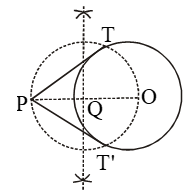 Step I: Take a point O in the plane of the paper and draw a circle of radius 3 cm.
Step I: Take a point O in the plane of the paper and draw a circle of radius 3 cm.
Step II: Mark a point P at a distance of 5.5 cm from the centre O and join OP.
Step III: Draw the right bisector of OP, intersecting OP at Q.
Step IV: Taking Q as centre and OQ = PQ as radius, draw a circle to intersect the given circle at T and T´.
Step V : Join PT and PT´ to get the required tangents.
Example 2: Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
Sol. In order to do the desired construction,
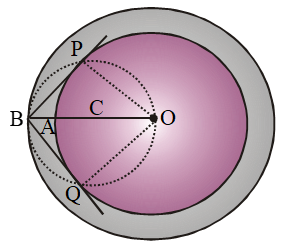 we follow the following steps:
we follow the following steps:
Step I: Take a point O on the plane of the paper and draw a circle of radius OA = 4 cm. Also, draw a concentric circle of radius OB = 6 cm.
Step II: Find the mid-point C of OB and draw a circle of radius OC = BC. Suppose this circle intersects the circle of radius 4 cm at P and Q.
Step III: Join BP and BQ to get the desired tangents from a point B on the circle of radius 6 cm.
By actual measurement, we find the
BP = BQ = 4.5 cm
Justification: In ∆BPO, we have
OB = 6 cm and OP = 4 cm
OB2= BP2 + OP2 [Using Pythagoras theorem]
\( \Rightarrow BP=\sqrt{O{{B}^{2}}-O{{P}^{2}}} \)
\( \Rightarrow \sqrt{36-16}=\sqrt{20}=4.47\simeq 4.5\text{ }cm~ \)
Similarly, BQ = 4.47cm ≈ 4.5 cm
Example 3: Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other an angle of 60º.
Sol. In order to draw the pair of tangents, we follow the following steps.
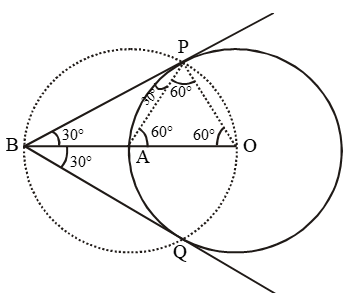 Step I: Take a point O on the plane of the paper and draw a circle of radius OA = 5 cm.
Step I: Take a point O on the plane of the paper and draw a circle of radius OA = 5 cm.
Step II: Produce OA to B such that OA = AB = 5 cm.
Step III: Taking A as the centre draw a circle of radius AO = AB = 5 cm. Suppose it cuts the circle drawn in step I at P and Q.
Step IV: Join BP and BQ to get the desired tangents.
Justification: In OAP, we have
OA = OP = 5 cm (= Radius) Also,
AP = 5 cm (= Radius of circle with centre A)
∴ ∆OAP is equilateral.
⇒ ∠PAO = 60º ⇒ ∠BAP = 120º
In ∆BAP, we have
BA = AP and ∠BAP = 120º
∴ ∠ABP = ∠APB = 30º ⇒ ∠PBQ = 60º
Example 4: Draw a circle of radius 3 cm. Draw a pair of tangents to this circle, which are inclined to each other at an angle of 60º.
Sol. Steps of construction
 Step I: Draw a circle with O as centre and radius = 3 cm.
Step I: Draw a circle with O as centre and radius = 3 cm.
Step II: Draw any diameter AOB of this circle.
Step III: Construct ∠BOC = 60º such that radius OC meets the circle at C.
Step IV: Draw AM ⊥ AB and CN ⊥OC.
Let AM and CN intersect each other at P.
Then, PA and PC are the desired tangents to the given circle, inclined at an angle of 60º
Proof: ∠AOC = (180º – 60º) = 120º
In quad. OAPC, we have
∠OAP = 90º, ∠AOC = 120º, ∠OCP = 90º.
∴∠APC = [360º – (90º + 120º + 90º)] = 60º.