Cones
Cones are three-dimensional closed surfaces.
In general use, the term cone refers to a right circular cone with its end closed to form a circular base surface. The vertex of the cone (the point) is not in the same plane as the base.
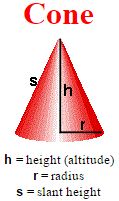Cones are not called polyhedra since their faces are not polygons. In many ways, however, a cone is similar to a pyramid. A cone’s base is simply a circle rather than a polygon as seen in the pyramid.
The volume of a cone can be calculated in the same manner as the volume of a pyramid: the volume is one-third the product of the base area times the height of the cone,
\(V=\frac { 1 }{ 3 } Bh\)
Since the base of a cone is a circle, the formula for the area of a circle can be substituted into the volume formula for B :
\(V=\frac { 1 }{ 3 } \pi { r }^{ 2 }h\)
(Volume of a cone: r = radius, h = height)
A net is a two-dimensional figure that can be cut out and folded up to make a three-dimensional solid.
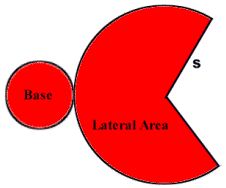Lateral = any face or surface that is not a base.
In a right circular cone, the slant height, s, can be found using the Pythagorean Theorem: \(s=\sqrt { { r }^{ 2 }+{ h }^{ 2 } } \)
The surface area (of a closed cone) is a combination of the lateral area and the area of the base. When cut along the slant side and laid flat, the surface of a cone becomes one circular base and the sector of a circle (lateral surface), as shown in the net at the left.
Note that the length of the arc in the sector is the same as the circumference of the small circular base.
By using a proportion, the area of the sector (lateral area) will be:
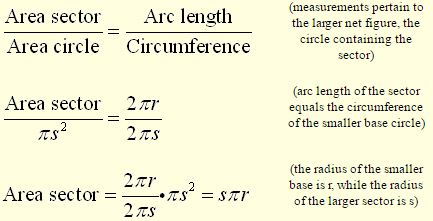The lateral area (sector) = sπr
The base area = area of a circle
SA = sπr + πr2 (Total Surface Area of a Closed Cone)
Note: The formula for the area of the sector (lateral area), , is equal to one half the product of the slant height and the circumference of the base.
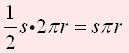
When working with surface areas of cones, read the questions carefully.
