What is Angle in Geometry
Angle
Angle: An angle is the union of two non-collinear rays with a common initial point.
When two rays have a common initial point, an angle is formed. The common initial point is called the vertex of the angle, and the two rays forming the angle are called the arms or sides of the angle. An angle is represented by the symbol ‘∠’.
The angles formed by the rays OA and OB is shown in figure below and is denoted by ∠BOA or ∠AOB
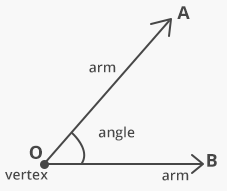For the sake of convenience the angle ∠BOA or ∠AOB can also be referred simply as ∠O. However, this cannot be done if there are more than one angle with the same vertex O. In such cases we can denote angles by the symbols such as ∠1, ∠2, ∠3, etc.
Naming an angle
Consider an angle as shown in Fig.
Using the symbol ∠, we can read or write an angle in three ways:
(i) ∠1 (By assigning a number)
(ii) ∠B (By its vertex)
(iii) ∠ABC or ∠CBA (By two points on each ray/arms and the vertex in the middle)
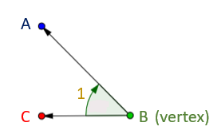Naming an angle by two points on its arms and the vertex is more useful, specially, when two or more angles have the vertex in common.
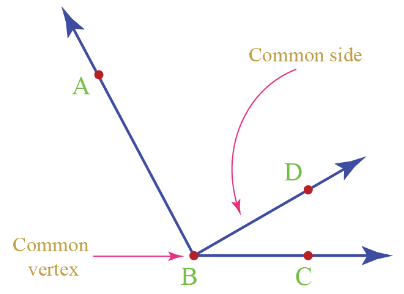Three angles are formed which have the same common vertex B.
These are:
(i) ∠ABC or ∠CBA
(ii) ∠ABD or ∠DBA
(iii) ∠DBC or ∠CBD
Exterior and interior of an angle
We have already discussed that any figure in a plane divides the plane into three parts. Similarly, when we draw an angle in a plane, it divides the triangle into three parts.
Interior of an angle: The interior of an angle BAC is the set of all points in its plane, which lie on the same side of AB as C and also on the same side of AC as B.
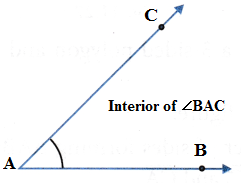
Exterior of an angle: The exterior of an angle BAC is the set of all points in its plane, which do not lie on the angle or in its interior.
Congruent angles: Two angles are said to be congruent if a trace copy of one can be superposed on the other to cover it completely and exactly.
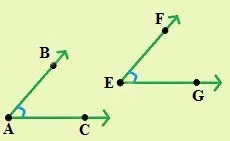
If ∠BAC is congruent of ∠FEG, then we write ∠BAC ≅ ∠FEG.
Adjacent angles
Two angles in a plane are said to be adjacent, if they have
(i) a common vertex,
(ii) a common arm, and
(iii) the other two non-common arms are on the opposite sides of the common arm.
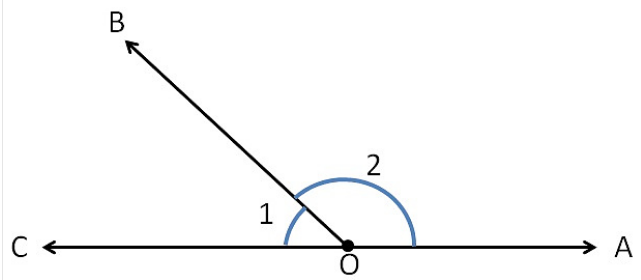
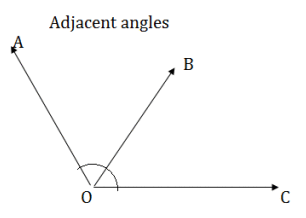In figure, ∠AOB and ∠BOC are adjacent angles because they have a common vertex O and a common arm OB. The other arms OC and OA are on the opposite sides of the common arm OB. Now, consider the following:
Linear pair: If the sum of ∠AOB and ∠BOC is 180°, then we say these two adjacent angles form a linear pair.
Magnitude of an angle
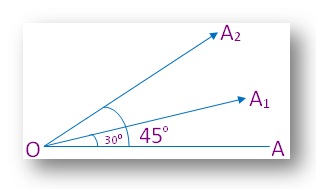
The size or magnitude of an angle depends upon the opening between its arms. It does not depend on the length of the arms. Two angles with different openings have different magnitudes.
Degree measure of an angle
Let us take a ray OA. Rotate it clockwise about the vertex O and reach point B. Thus, OA becomes the initial position and OB the final position. In this case ∠AOB is formed. Rotation can be either in clockwise direction or anti-clockwise.
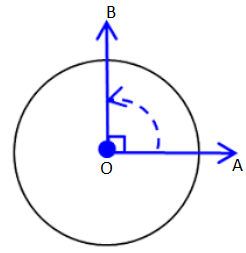A complete rotation is divided into 360 equal parts and each part is equal to one degree. In this way, one complete rotation is of 360°. Angles are measured in terms of degrees denoted by °. This symbol is inserted on the right top of the numeral, representing the opening of an angle.
Example: 30 degrees can be written as 30°.