How Do You Get The Perimeter Of A Shape
Rohan and his father are watching their garden. They want to fence it with barbed wire to make it safe. Before going to the market to purchase the wire, his father wants to know the length of the wire needed. To measure the length, he starts from a point on the boundary of the garden and keeps moving the measuring tape along the boundary line and reaches the initial point. That means he has made a complete round of the garden and the length of the measuring tape is equal to the distance covered in one full round. This length of the tape is the perimeter of the garden.
PERIMETER
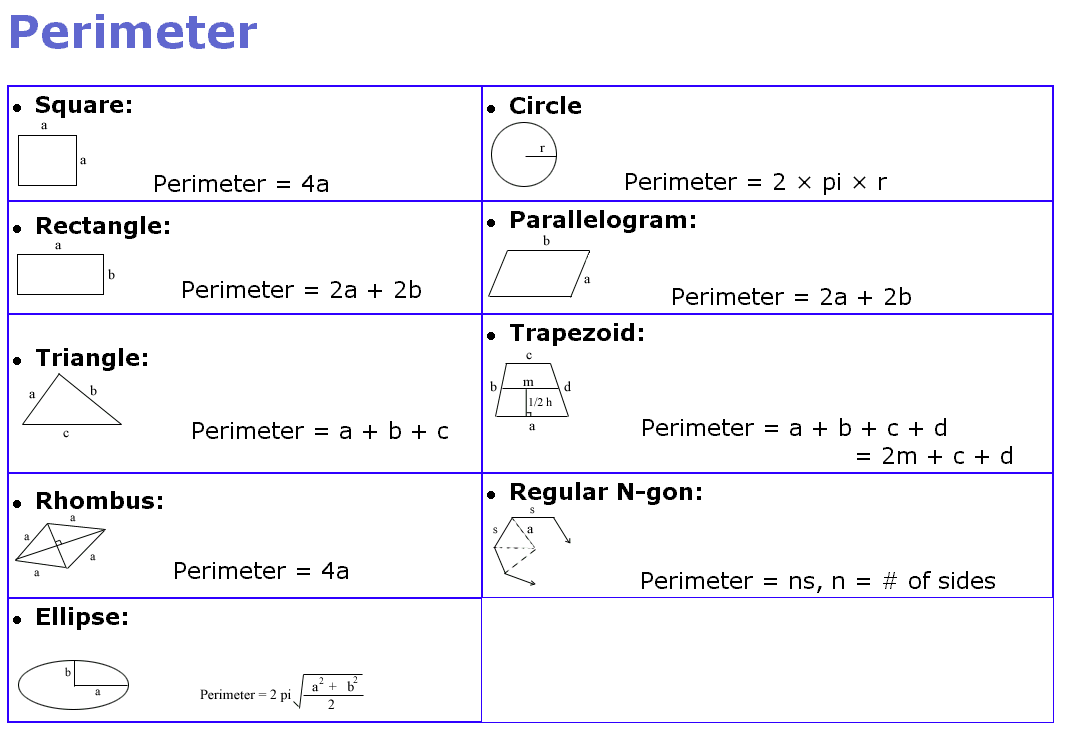
Perimeter of a closed figure is the total length of its boundary.
We know that all polygons (triangle, square, rectangle, pentagon, hexagon, etc) are rectilinear figures.
∴ Perimeter = Sum of the lengths of its all sides
Perimeter of a triangle
Perimeter of a triangle ABC is the sum of the lengths of its sides. If the lengths of the sides of a triangle are a, b, and c, then
Perimeter = AB + BC + CA
= c + a + b = a + b + c
Perimeter of a square
The perimeter of a square ABCD is the total lengths of its all equal sides. If the length of each side is s then,
Perimeter = AB + BC + CD + DA
= s + s + s + s = 4s
Perimeter of a rectangle
The perimeter of a rectangle ABCD is the double of the sum of its two adjacent sides. If the lengths of its two adjacent sides are l and b, then,
Perimeter = AB + BC + CD + DA
= l + b + l + b
= 2l + 2b
= 2(l + b)
Shapes of different kinds with the same perimeter
We can have different kinds of shapes with the same perimeter. To understand this, let us take a string 32 cm long. What figures can we make by using this string?
We can make an isosceles triangle of side 10 cm, 10 cm, and 12 cm.
∴ P = AB + BC + CA
= 10 cm + 10 cm + 12 cm = 32 cm
By using a 32 cm string, we can make a square of side 8 cm.
P = AB + BC + CD + DA
= 8 cm + 8 cm + 8 cm + 8 cm
= 4 × 8 cm = 32 cm
By using the same string, we can make a rectangle of length 10 cm and breadth 6 cm.
P = AB + BC + CD + DA
= 6 cm + 10 cm + 6 cm + 10 cm = 32 cm
We see that in all the three cases, the perimeter is 32 cm but they have different shapes. Hence we can conclude that different kinds of shapes can have the same perimeter.
Example 1: Find the perimeter of a rectangular plot whose length is 15 m and breadth is 850 cm. Solution: Length of the rectangle = 15 m
Breadth of the rectangle = 850 cm
= 850/100 m (1 m = 100 cm)
= 8.5 m
∴ Perimeter of the rectangular plot = 2 (Length + Breadth)
= 2 (l + b)
= 2 (15 + 8.5)
= 2 × 23.5 = 47.0 m
Example 2: Find the perimeter of the given figure.
Solution: Perimeter
= AB + BC + CD + DE + EF + FG + GA
= 3.2 cm + 1.5 cm + 5 cm + 5 cm + 1.5 cm + 3.2 cm + 2 cm
= 21.4 cm
Example 3: Find the length of a string used to make a triangle ABC. If the same string is used to make a square, what will be the side of the square?
Solution: Perimeter of triangle ABC
= Length of the string = AB + BC + CA
= 6 cm + 12 cm + 10 cm 28 cm
Now, the same string is used to make a square. So the perimeter of a square will be 28 cm.
Perimeter of a square
= 4 × side
28 cm = 4 × side
side = 28/4 = 7 cm
Hence, the side of a square will be 7 cm.
Example 4: The perimeter of a rectangular field is 260 m. If its length is 90 m,find its breadth.
Solution: Perimeter of a rectangle
= 2 (b + l)
260 m = 2 (b + 90 m)
260 m = 2 b + 180 m
(260 – 180) m = 2b
80 m = 2b
b = 80/2 m
b = 40 m
Hence, the breadth of the rectangular field
= 40 m.