Function Transformations
There are numerous ways to apply transformations to functions to create new functions.
Let’s look at some of the possibilities. Remember to utilize your graphing calculator to compare the graphs of your functions and their transformations.
Reflections and Functions: Examining -f (x) and f (-x)
Reflection over the x-axis
-f (x) reflects f (x) over the x-axis.
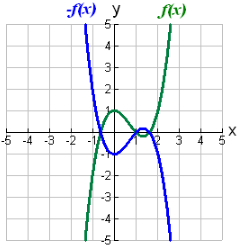A reflection is a mirror image. Placing the edge of a mirror on the x-axis will form a reflection in the x-axis. This can also be thought of as “folding” over the x-axis.
If the original (parent) function is y = f (x), the reflection over the x-axis is function -f (x).
Reflection over the y-axis
f (-x) reflects f (x) over the y-axis.
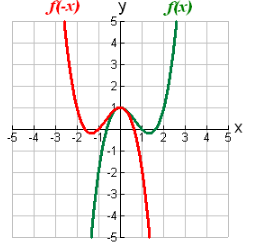Placing the edge of a mirror on the y-axis will form a reflection in the y-axis. This can also be thought of as “folding” over the y-axis.
If the original (parent) function is y = f (x), the reflection over the y-axis is function f (-x).
Translations and Functions: Examining f (x + a) and f (x) + a
Slide to the right or left
f (x + a) translates f (x) horizontally
If the original (parent) function is y = f (x), the translation (sliding) of the function horizontally to the left or right is given by the function f (x – a).
if a > 0, the graph translates (slides) to the right.
if a < 0, the graph translates (slides) to the left.
Remember that you are “subtracting” the value of a from x. Thus f (x + 2) is really f (x – (-2)) and the graph moves to the left.
Slide upward or downward
f (x)+ a translates f (x) vertically
If the original (parent) function is y = f (x), the translation (sliding) of the function vertically upward or downward is the function f (x) + a.
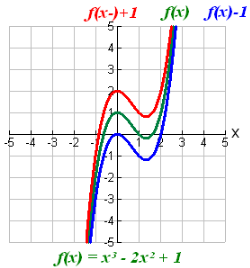if a > 0, the graph translates (slides) upward.
if a < 0, the graph translates (slides) downward.
Remember that you are adding the value of a to the y-values of the function.
Stretch or Compress Functions: Examining f (ax) and a f (x)
Horizontal Stretch or Compress
f (ax) stretches/compresses f (x) horizontally
A horizontal stretching is the stretching of the graph away from the y-axis.
A horizontal compression is the squeezing of the graph towards the y-axis.
If the original (parent) function is y = f (x), the horizontal stretching or compressing of the function is the function f (ax).
if 0 < a < 1 (a fraction), the graph is stretched horizontally by a factor
of a units.
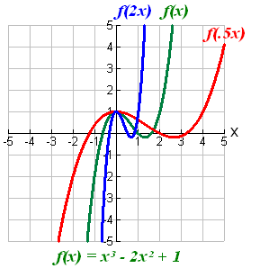
if a > 1, the graph is compressed horizontally by a factor of a units.
if a should be negative, the horizontal compression or horizontal stretching of the graph is followed by a reflection of the graph across the y-axis.
Vertical Stretch or Compress
a f (x) stretches/compresses f (x) vertically
A vertical stretching is the stretching of the graph away from the x-axis.
A vertical compression is the squeezing of the graph towards the x-axis.
If the original (parent) function is y = f (x), the vertical stretching or compressing of the function is the function a f(x).
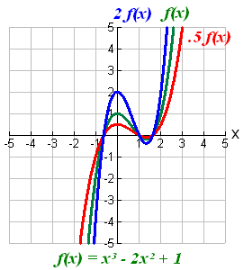if 0 < a < 1 (a fraction), the graph is compressed vertically by a factor
of a units.
if a > 1, the graph is stretched vertically by a factor of a units.
If a should be negative, then the vertical compression or vertical stretching of the graph is followed by a reflection across the x-axis.