The Binomial Theorem
You are faced with the problem of expanding \((x+y)^10\) . What to do??? Do you really have to multiply this expression times itself 10 times?? That could take forever.

Let’s investigate:
When binomial expressions are expanded, is there any type of pattern developing which might help us expand more quickly? Consider the following expansions:
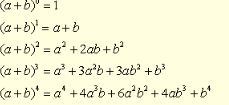
What observations can we make in general about the expansion of \((a+b)^n\)
1. The expansion is a series (an adding of terms).
2. The number of terms in each expansion is one more than n. (terms = n + 1)
3. The power of a starts with an and decreases by one in each successive term ending with a0. The power of b starts with b0 and increases by one in each successive term ending with bn.
4. The power of b is always one less than the “number” of the term. The power of a is always n minus the power of b.
5. The sum of the exponents in each term adds up to n.
6. The coefficients of the first and last terms are each one.
7. The coefficients of the middle terms form an interesting (but perhaps not easily recognized) pattern where each coefficient can be determined from the previous term. The coefficient is the product of the previous term’s coefficient and a’s index, divided by the number of that previous term.
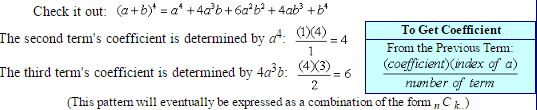
8. Another famous pattern is also developing regarding the coefficients. If the coefficients are “pulled off” of the terms and arranged, they form a triangle known as Pascal’s triangle. (The use of Pascal’s triangle to determine coefficients can become tedious when the expansion is to a large power.)
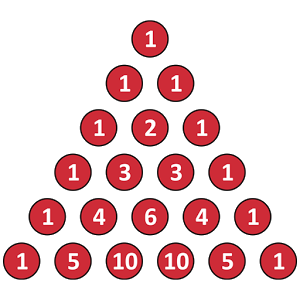
(The two outside edges of the triangle are comprised of ones. The other terms are each the sum of the two terms immediately above them in the triangle.)
By pulling these observations together with some mathematical syntax, a theorem is formed relating to the expansion of binomial terms:


Examples using the Binomial Theorem:

