Selina Concise Mathematics Class 10 ICSE Solutions Ratio and Proportion (Including Properties and Uses)

Selina Concise Mathematics Class 10 ICSE Solutions Ratio and Proportion (Including Properties and Uses)

Selina Publishers Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion (Including Properties and Uses)

Ratio and Proportion Exercise 7A – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.

Solution:

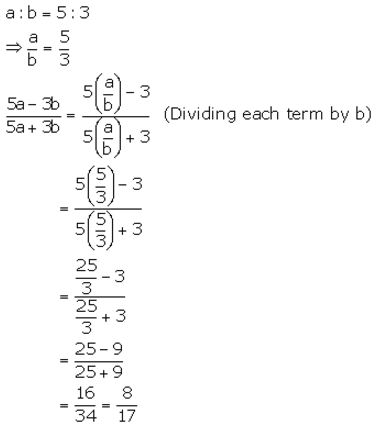
Question 2.
If x: y = 4: 7, find the value of (3x + 2y): (5x + y).
Solution:

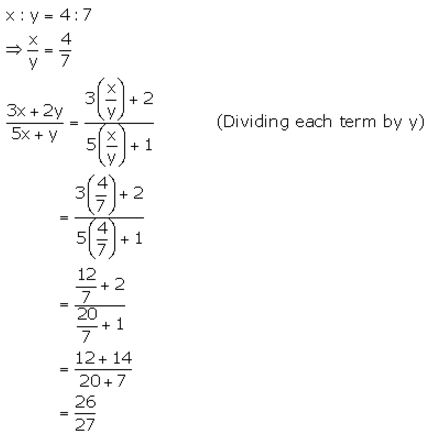
Question 3.

Solution:

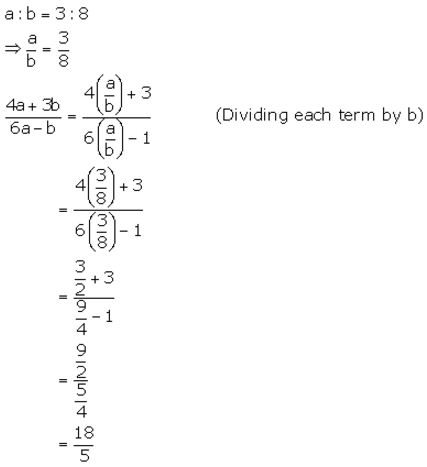
Question 4.
If (a – b): (a + b) = 1: 11, find the ratio (5a + 4b + 15): (5a – 4b + 3).
Solution:

Question 5.

Solution:

Question 6.

Solution:

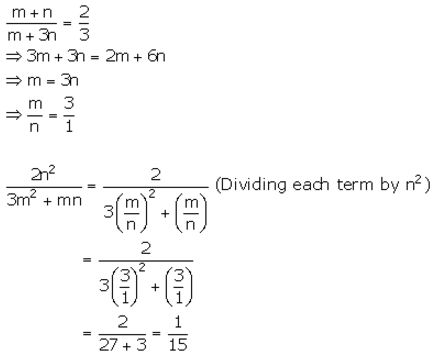
Question 7.

Solution:

Question 8.

Solution:

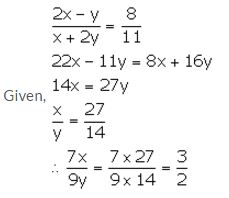
Question 9.

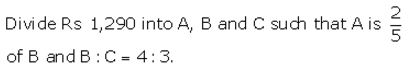
Solution:

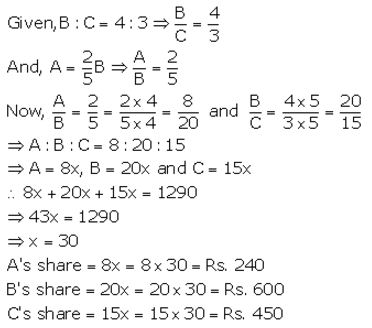
Question 10.
A school has 630 students. The ratio of the number of boys to the number of girls is 3 : 2. This ratio changes to 7 : 5 after the admission of 90 new students. Find the number of newly admitted boys.
Solution:

Question 11.
What quantity must be subtracted from each term of the ratio 9: 17 to make it equal to 1: 3?
Solution:
Let x be subtracted from each term of the ratio 9: 17.

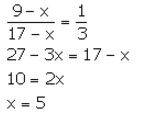
Thus, the required number which should be subtracted is 5.

Question 12.
The monthly pocket money of Ravi and Sanjeev are in the ratio 5 : 7. Their expenditures are in the ratio 3 : 5. If each saves Rs. 80 every month, find their monthly pocket money.
Solution:

Question 13.
The work done by (x – 2) men in (4x + 1) days and the work done by (4x + 1) men in (2x – 3) days are in the ratio 3: 8. Find the value of x.
Solution:
Assuming that all the men do the same amount of work in one day and one day work of each man = 1 units, we have,
Amount of work done by (x – 2) men in (4x + 1) days
= Amount of work done by (x – 2)(4x + 1) men in one day
= (x – 2)(4x + 1) units of work
Similarly,
Amount of work done by (4x + 1) men in (2x – 3) days
= (4x + 1)(2x – 3) units of work
According to the given information,

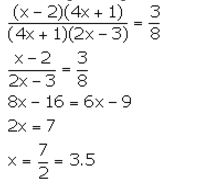
Question 14.
The bus fare between two cities is increased in the ratio 7: 9. Find the increase in the fare, if:
(i) the original fare is Rs 245;
(ii) the increased fare is Rs 207.
Solution:

Question 15.
By increasing the cost of entry ticket to a fair in the ratio 10: 13, the number of visitors to the fair has decreased in the ratio 6: 5. In what ratio has the total collection increased or decreased?
Solution:
Let the cost of the entry ticket initially and at present be 10 x and 13x respectively.
Let the number of visitors initially and at present be 6y and 5y respectively.
Initially, total collection = 10x × 6y = 60 xy
At present, total collection = 13x × 5y = 65 xy
Ratio of total collection = 60 xy: 65 xy = 12: 13
Thus, the total collection has increased in the ratio 12: 13.

Question 16.
In a basket, the ratio between the number of oranges and the number of apples is 7: 13. If 8 oranges and 11 apples are eaten, the ratio between the number of oranges and the number of apples becomes 1: 2. Find the original number of oranges and the original number of apples in the basket.
Solution:
Let the original number of oranges and apples be 7x and 13x.
According to the given information,

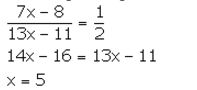
Thus, the original number of oranges and apples are 7 × 5 = 35 and 13 × 5 = 65 respectively.

Question 17.
In a mixture of 126 kg of milk and water, milk and water are in ratio 5 : 2. How much water must be added to the mixture to make this ratio 3 : 2?
Solution:

Question 18.
(A) If A: B = 3: 4 and B: C = 6: 7, find:
(i) A: B: C
(ii) A: C
(B) If A : B = 2 : 5 and A : C = 3 : 4, find
(i) A : B : C
Solution:

Question 19(i).
If 3A = 4B = 6C; find A: B: C.
Solution:

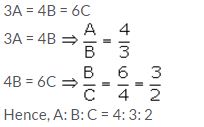
Question 19(ii).
If 2a = 3b and 4b = 5c, find: a : c.
Solution:

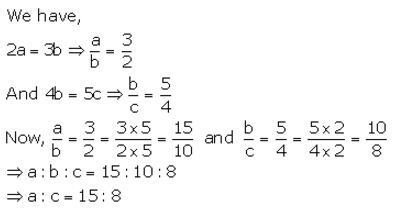
Question 20.

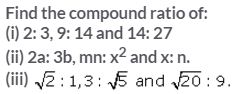
Solution:

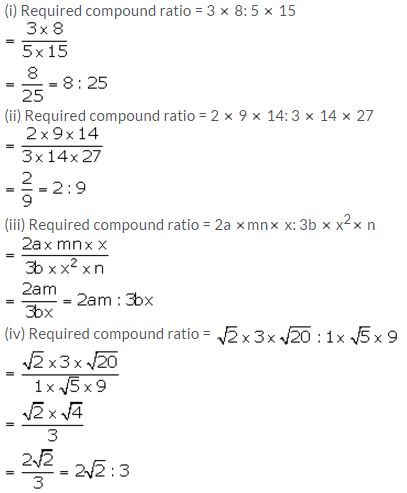
Question 21.
Find duplicate ratio of:
(i) 3: 4 (ii) 3√3 : 2√5
Solution:
(i) Duplicate ratio of 3 : 4 = 32 : 42 = 9 : 16
(ii) Duplicate ratio of 3√3 : 2√5 = (3√3)² : (2√5)² = 27 : 20

Question 22.

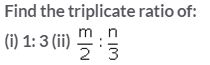
Solution:

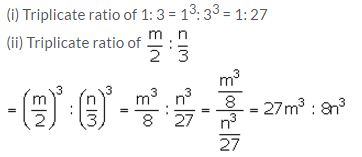
Question 23.
Find sub-duplicate ratio of:
(i) 9: 16 (ii) (x – y)⁴: (x + y)⁶
Solution:

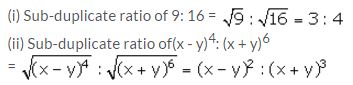
Question 24.
Find the sub-triplicate ratio of:
(i) 64: 27 (ii) x³: 125y³
Solution:
(i) Sub-triplicate ratio of 64 : 27 = ∛64 : ∛27 = 4 : 3
(ii) Sub-triplicate ratio of x³ : 125y³ = ∛x³ : ∛125y³ = x : 5y

Question 25.

Solution:

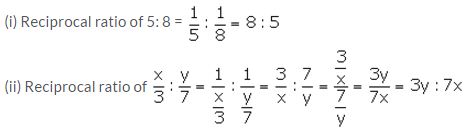
Question 26.
If (x + 3) : (4x + 1) is the duplicate ratio of 3 : 5, find the value of x.
Solution:

Question 27.
If m: n is the duplicate ratio of m + x: n + x; show that x² = mn.
Solution:

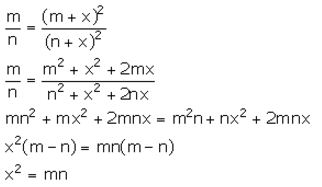
Question 28.
If (3x – 9) : (5x + 4) is the triplicate ratio of 3 : 4, find the value of x.
Solution:

Question 29.
Find the ratio compounded of the reciprocal ratio of 15: 28, the sub-duplicate ratio of 36: 49 and the triplicate ratio of 5: 4.
Solution:

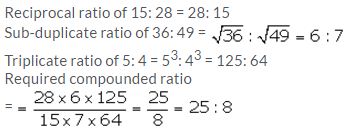
Question 30(a).
If r² ₌pq, show that p : q is the duplicate ratio of (p + r) : (q + r).
Solution:

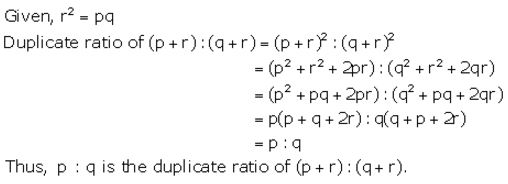
Question 30(b).

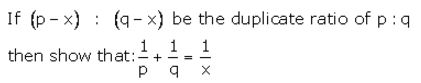
Solution:

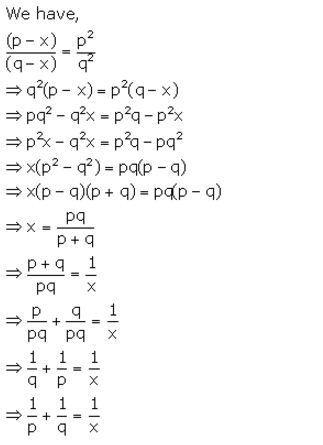
Ratio and Proportion Exercise 7B – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.
Find the fourth proportional to:
(i) 1.5, 4.5 and 3.5 (ii) 3a, 6a² and 2ab²
Solution:
(i) Let the fourth proportional to 1.5, 4.5 and 3.5 be x.
⇒ 1.5 : 4.5 = 3.5 : x
⇒ 1.5 × x = 3.5 4.5
⇒ x = 10.5
(ii) Let the fourth proportional to 3a, 6a² and 2ab² be x.
⇒ 3a : 6a² = 2ab² : x
⇒ 3a × x = 2ab² 6a²
⇒ 3a × x = 12a³b²
⇒ x = 4a²b²

Question 2.

Solution:

Question 3.

Solution:
(i) Let the mean proportional between 6 + 3√3 and 8 – 4√3 be x.
⇒ 6 + 3√3, x and 8 – 4√3 are in continued proportion.
⇒ 6 + 3√3 : x = x : 8 – 4√3
⇒ x × x = (6 + 3√3) (8 – 4√3)
⇒ x² = 48 + 24√3- 24√3 – 36
⇒ x² = 12
⇒ x = 2√3
(ii) Let the mean proportional between a – b and a³ – a²b be x.
⇒ a – b, x, a³ – a²b are in continued proportion.
⇒ a – b : x = x : a³ – a²b
⇒ x × x = (a – b) (a³ – a²b)
⇒ x² = (a – b) a²(a – b) = [a(a – b)]²
⇒ x = a(a – b)

Question 4.
If x + 5 is the mean proportional between x + 2 and x + 9; find the value of x.
Solution:
Given, x + 5 is the mean proportional between x + 2 and x + 9.
⇒ (x + 2), (x + 5) and (x + 9) are in continued proportion.
⇒ (x + 2) : (x + 5) = (x + 5) : (x + 9)
⇒ (x + 5)² = (x + 2)(x + 9)
⇒ x² + 25 + 10x = x² + 2x + 9x + 18
⇒ 25 – 18 = 11x – 10x
⇒ x = 7

Question 5.
If x², 4 and 9 are in continued proportion, find x.
Solution:

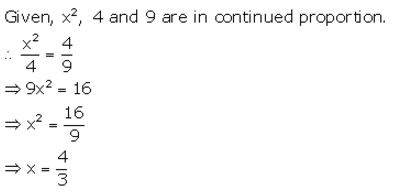
Question 6.
What least number must be added to each of the numbers 6, 15, 20 and 43 to make them proportional?
Solution:

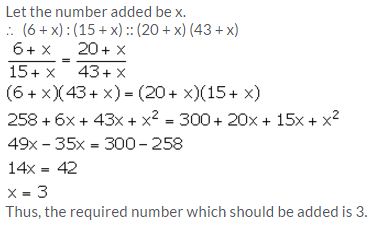
Question 7(i).

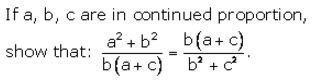
Solution:

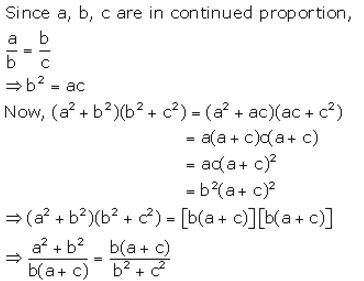
Question 7(ii).

Solution:

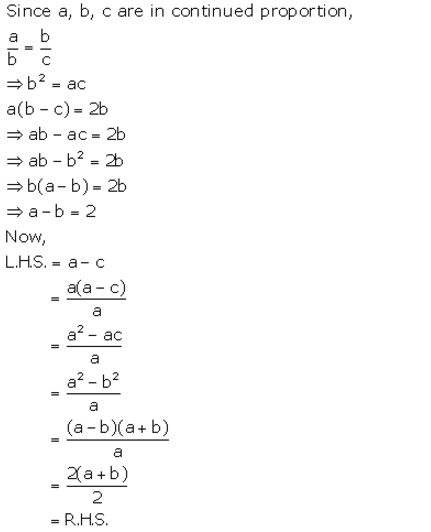
Question 7(iii).

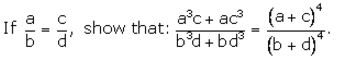
Solution:

Question 8.
What least number must be subtracted from each of the numbers 7, 17 and 47 so that the remainders are in continued proportion?
Solution:

Question 9.
If y is the mean proportional between x and z; show that xy + yz is the mean proportional between x²+y² and y²+z².
Solution:
Since y is the mean proportion between x and z
Therefore, y² = xz
Now, we have to prove that xy+yz is the mean proportional between x²+y² and y²+z², i.e.,

LHS = RHS
Hence, proved.

Question 10.
If q is the mean proportional between p and r, show that:
pqr (p + q + r)³ = (pq + qr + rp)³.
Solution:
Given, q is the mean proportional between p and r.
⇒ q² = pr

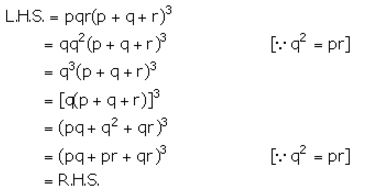
Question 11.
If three quantities are in continued proportion; show that the ratio of the first to the third is the duplicate ratio of the first to the second.
Solution:
Let x, y and z be the three quantities which are in continued proportion.
Then, x : y :: y : z ⇒ y² = xz ….(1)
Now, we have to prove that
x : z = x² : y²
That is we need to prove that
xy² = x²z
LHS = xy² = x(xz) = x²z = RHS [Using (1)]
Hence, proved.

Question 12.

Solution:
Given, y is the mean proportional between x and z.
⇒ y² = xz

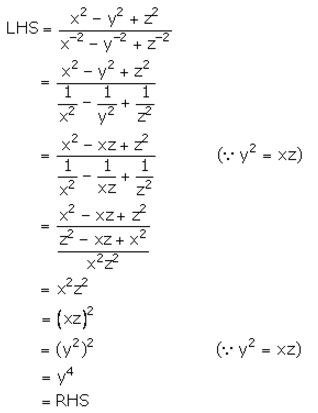
Question 13.

Solution:

Question 14.
Find two numbers such that the mean mean proportional between them is 12 and the third proportional to them is 96.
Solution:

Question 15.

Solution:

Question 16.
If p: q = r: s; then show that:
mp + nq : q = mr + ns : s.
Solution:

Question 17.

Solution:

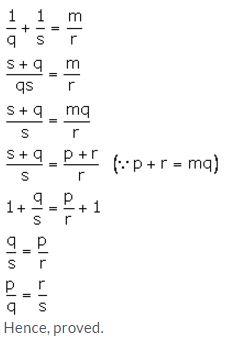
Question 18.

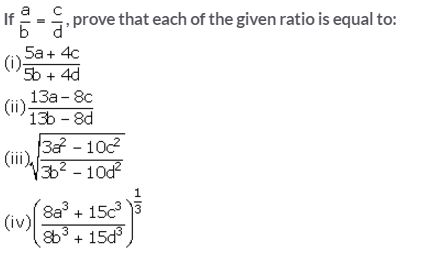
Solution:

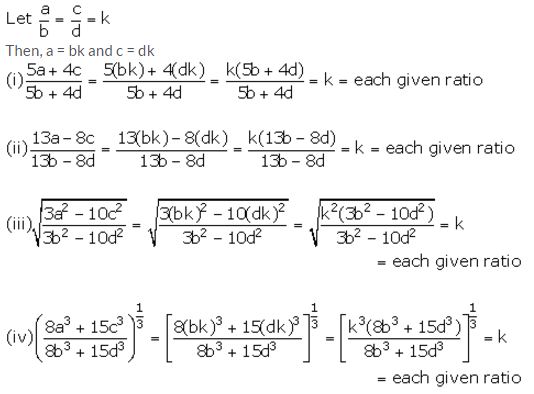
Question 19.

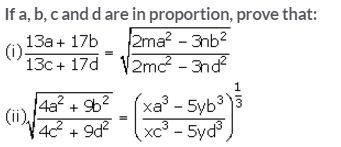
Solution:

Question 20.

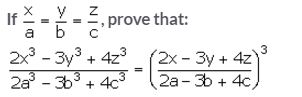
Solution:

Ratio and Proportion Exercise 7C – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.
If a : b = c : d, prove that:
(i) 5a + 7b : 5a – 7b = 5c + 7d : 5c – 7d.
(ii) (9a + 13b) (9c – 13d) = (9c + 13d) (9a – 13b).
(iii) xa + yb : xc + yd = b : d.
Solution:

Question 2.
If a : b = c : d, prove that:
(6a + 7b) (3c – 4d) = (6c + 7d) (3a – 4b).
Solution:

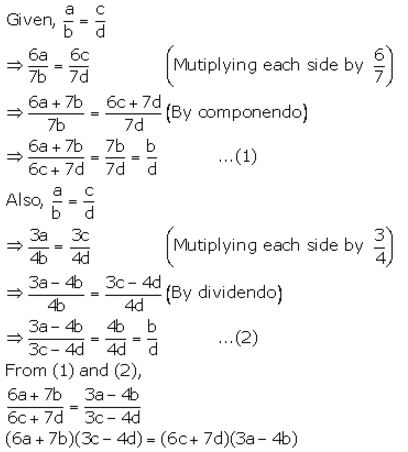
Question 3.

Solution:

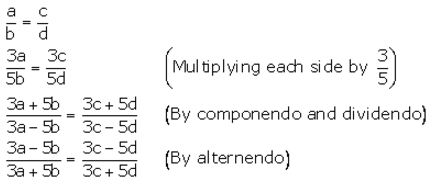
Question 4.

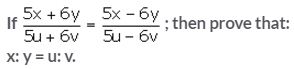
Solution:

Question 5.
If (7a + 8b) (7c – 8d) = (7a – 8b) (7c + 8d), prove that a: b = c: d.
Solution:

Question 6.

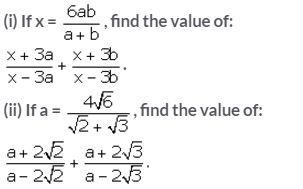
Solution:

Question 7.
If (a + b + c + d) (a – b – c + d) = (a + b – c – d) (a – b + c – d), prove that a: b = c: d.
Solution:

Question 8.

Solution:

Question 9.

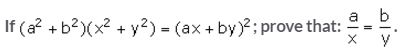
Solution:

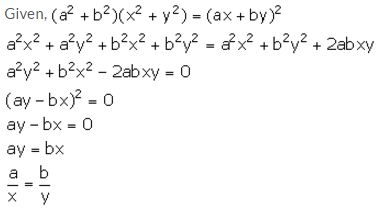
Question 10.

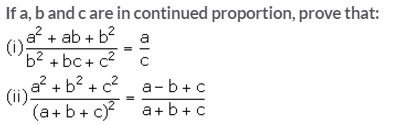
Solution:
Given, a, b and c are in continued proportion.

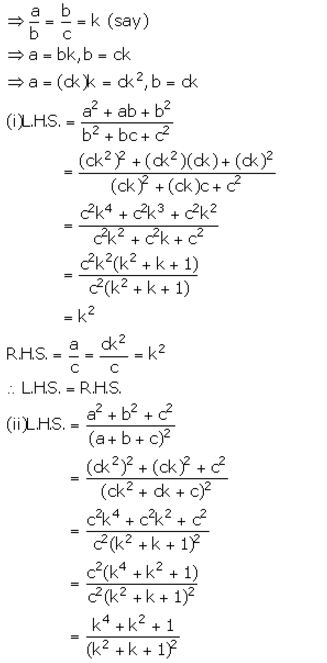
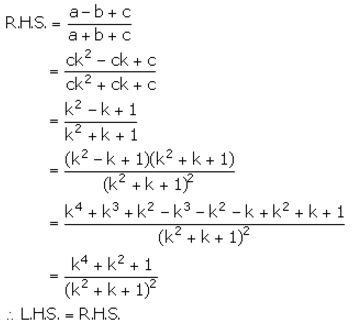
Question 11.

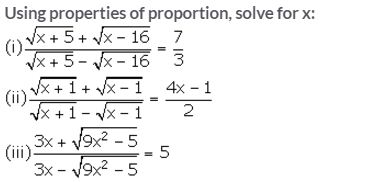
Solution:

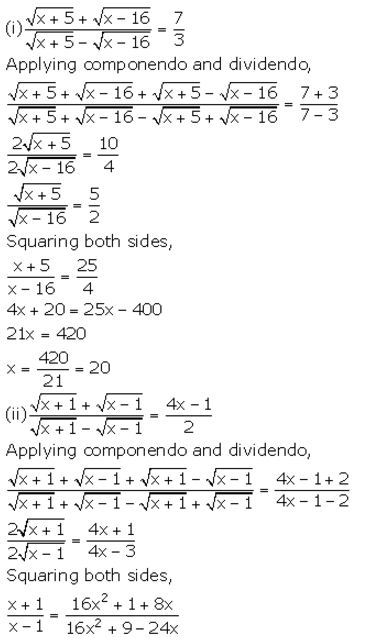
Question 12.

Solution:

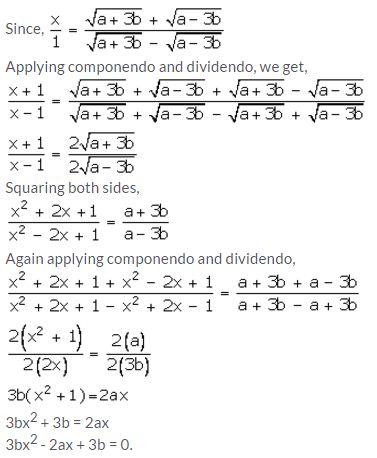
Question 13.

Solution:

Question 14.

Solution:

Question 15.

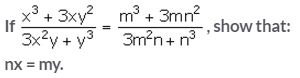
Solution:

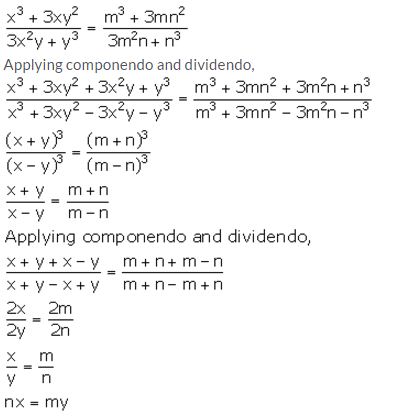
Ratio and Proportion Exercise 7D – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.
If a: b = 3: 5, find:
(10a + 3b): (5a + 2b)
Solution:

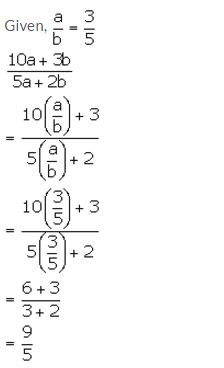
Question 2.
If 5x + 6y: 8x + 5y = 8: 9, find x: y.
Solution:

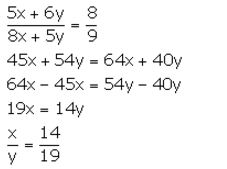
Question 3.
If (3x – 4y): (2x – 3y) = (5x – 6y): (4x – 5y), find x: y.
Solution:

Question 4.
Find the:
(i) duplicate ratio of 2√2 : 3√5
(ii) triplicate ratio of 2a: 3b
(iii) sub-duplicate ratio of 9x²a⁴ : 25y⁶b²
(iv) sub-triplicate ratio of 216: 343
(v) reciprocal ratio of 3: 5
(vi) ratio compounded of the duplicate ratio of 5: 6, the reciprocal ratio of 25: 42 and the sub-duplicate ratio of 36: 49.
Solution:

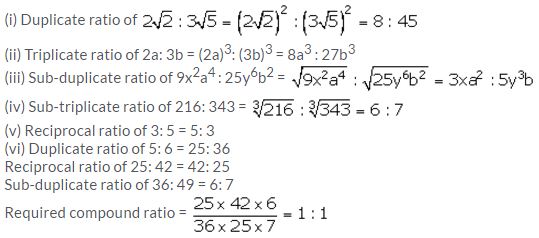
Question 5.
Find the value of x, if:
(i) (2x + 3): (5x – 38) is the duplicate ratio of √5 : √6
(ii) (2x + 1): (3x + 13) is the sub-duplicate ratio of 9: 25.
(iii) (3x – 7): (4x + 3) is the sub-triplicate ratio of 8: 27.
Solution:

Question 6.
What quantity must be added to each term of the ratio x: y so that it may become equal to c: d?
Solution:
Let the required quantity which is to be added be p.
Then, we have:

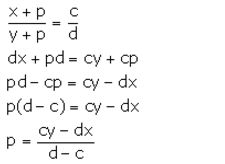
Question 7.
A woman reduces her weight in the ratio 7 : 5. What does her weight become if originally it was 84 kg?
Solution:

Question 8.
If 15(2x² – y²) = 7xy, find x: y; if x and y both are positive.
Solution:

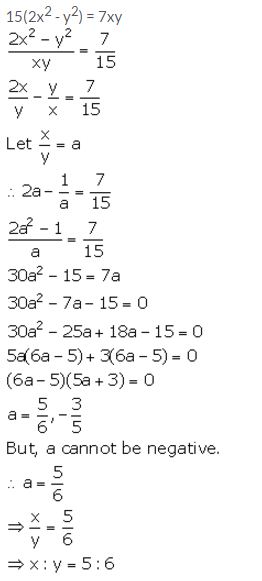
Question 9.
Find the:
(i) fourth proportional to 2xy, x² and y².
(ii) third proportional to a² – b² and a + b.
(iii) mean proportional to (x – y) and (x³ – x²y).
Solution:

Question 10.
Find two numbers such that the mean proportional between them is 14 and third proportional to them is 112.
Solution:

Question 11.
If x and y be unequal and x: y is the duplicate ratio of x + z and y + z, prove that z is mean proportional between x and y.
Solution:

Question 12.

Solution:

Question 13.
If (4a + 9b) (4c – 9d) = (4a – 9b) (4c + 9d), prove that:
a: b = c: d.
Solution:

Question 14.

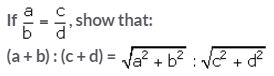
Solution:

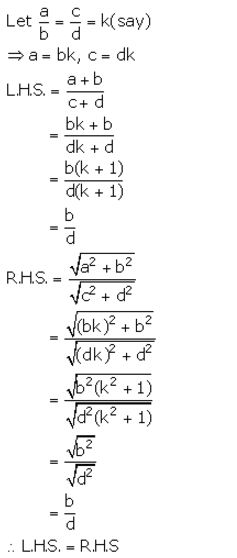
Question 15.
There are 36 members in a student council in a school and the ratio of the number of boys to the number of girls is 3: 1. How any more girls should be added to the council so that the ratio of the number of boys to the number of girls may be 9: 5?
Solution:
Ratio of number of boys to the number of girls = 3: 1
Let the number of boys be 3x and number of girls be x.
3x + x = 36
4x = 36
x = 9
∴ Number of boys = 27
Number of girls = 9
Le n number of girls be added to the council.
From given information, we have:

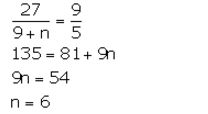
Thus, 6 girls are added to the council.

Question 16.
If 7x – 15y = 4x + y, find the value of x: y. Hence, use componendo and dividend to find the values of:

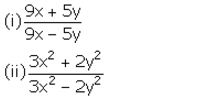
Solution:

Question 17.

Solution:

Question 18.

Solution:

Question 19.

Solution:

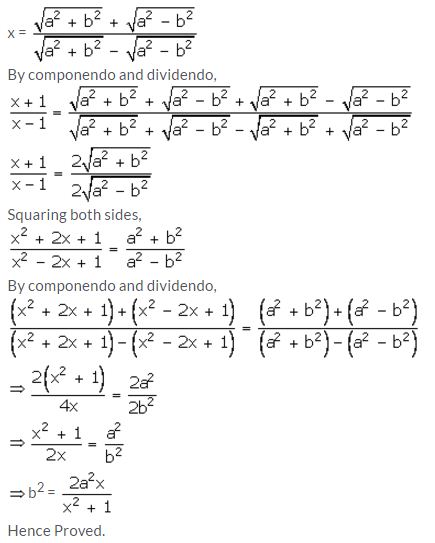
Question 20.

Solution:

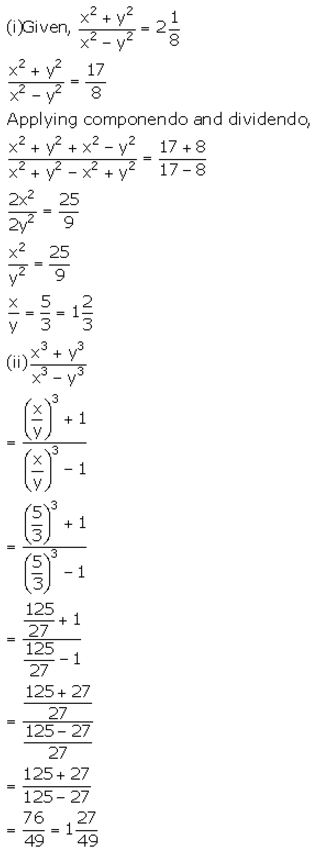
Question 21.

Solution:

Question 22.

Solution:

Question 23.

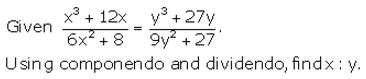
Solution:

Question 24.

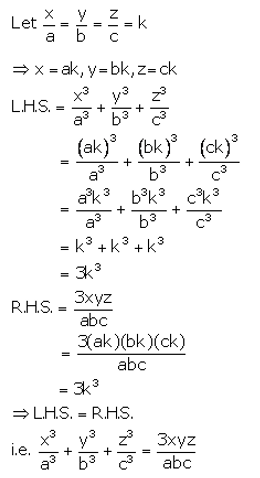
Question 25.

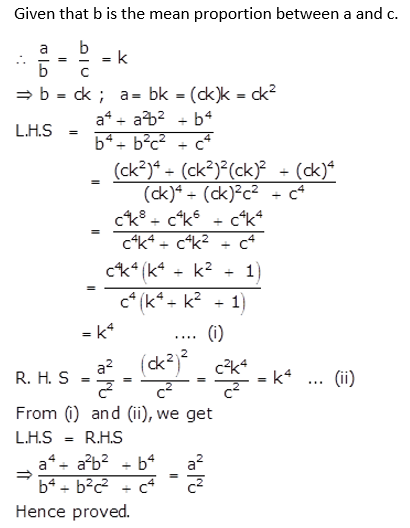
Question 26.

Question 27.

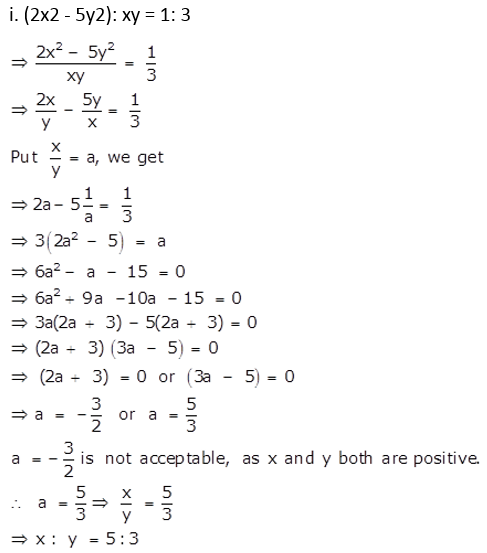
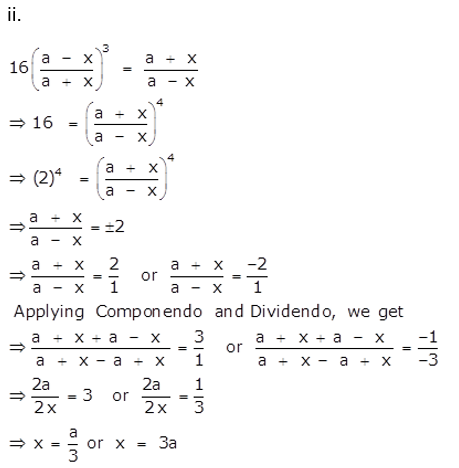
Question 28.

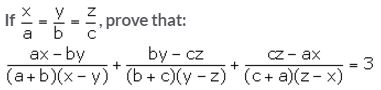
Solution:

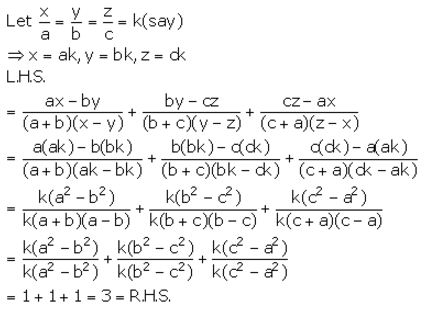
Question 29.

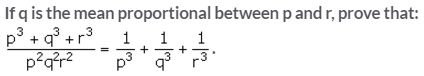
Solution:
Since, q is the mean proportional between p and r,
q² = pr

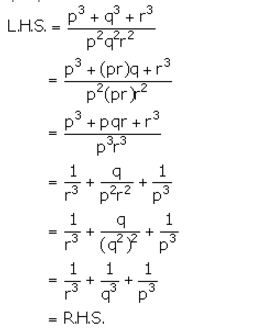
Question 30.
If a, b and c are in continued proportion, prove that:
a: c = (a² + b²) : (b² + c²)
Solution:

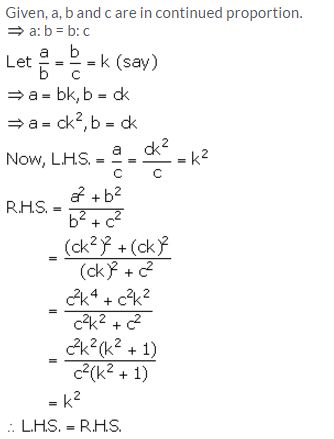
More Resources for Selina Concise Class 10 ICSE Solutions

• Selina ICSE Class 10 Maths Solutions
• Concise Physics Class 10 ICSE Answers
• Concise Chemistry Class 10 ICSE Answers
• Concise Biology Class 10 ICSE Answers

ICSE Solutions Selina ICSE Solutions