Selina Concise Mathematics Class 10 ICSE Solutions Banking (Recurring Deposit Accounts)

Selina Concise Mathematics Class 10 ICSE Solutions Banking (Recurring Deposit Accounts)

Selina Publishers Concise Mathematics Class 10 ICSE Solutions Chapter 2 Banking (Recurring Deposit Accounts)

Banking (Recurring Deposit Accounts) Exercise 2A – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.
Manish opens a Recurring Deposit Account with the Bank of Rajasthan and deposits ₹ 600 per month for 20 months. Calculate the maturity value of this account, if the bank pays interest at the rate of 10% per annum.
Solution:
Installment per month(P) = ₹ 600
Number of months(n) = 20
Rate of interest(r) = 10% p.a.

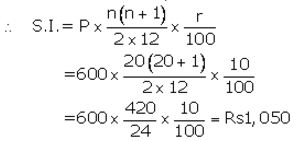
The amount that Manish will get at the time of maturity
= ₹ (600×20) + ₹ 1,050
= ₹ 12,000 + ₹ 1,050
= ₹ 13,050

Question 2.
Mrs. Mathew opened a Recurring Deposit Account in a certain bank and deposited ₹ 640 per month for 4 ½ years. Find the maturity value of this account, if the bank pays interest at the rate of 12% per year.
Solution:
Installment per month(P) = ₹ 640
Number of months(n) = 54
Rate of interest(r)= 12% p.a.

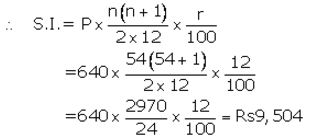
The amount that Manish will get at the time of maturity
= ₹ (640×54)+ ₹ 9,504
= ₹ 34,560 + ₹ 9,504
= ₹ 44,064

Question 3.
Each of A and B both opened recurring deposit accounts in a bank. If A deposited ₹ 1,200 per month for 3 years and B deposited ₹ 1,500 per month for 2 ½ years; find, on maturity, who will get more amount and by how much? The rate of interest paid by the bank is 10% per annum.
Solution:
For A
Installment per month(P) = ₹ 1,200
Number of months(n) = 36
Rate of interest(r) = 10% p.a.

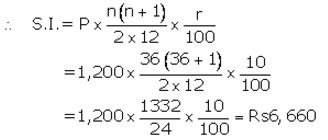
The amount that A will get at the time of maturity
= ₹ (1,200×36) + ₹ 6,660
= ₹ 43,200 + ₹ 6,660
= ₹ 49,860
For B
Instalment per month(P) = ₹ 1,500
Number of months(n) = 30
Rate of interest(r) = 10% p.a.

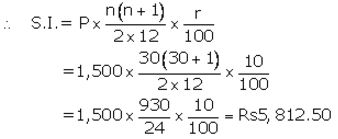
The amount that B will get at the time of maturity
= ₹ (1,500×30) + ₹ 5,812.50
= ₹ 45,000 + ₹ 5,812.50
= ₹ 50,812.50
Difference between both amounts = ₹ 50,812.50 – ₹ 49,860
= ₹ 952.50
Then B will get more money than A by ₹ 952.50.

Question 4.
Ashish deposits a certain sum of money every month is a Recurring Deposit Account for a period of 12 months. If the bank pays interest at the rate of 11% p.a. and Ashish gets ₹ 12,715 as the maturity value of this account, what sum of money did money did he pay every month?
Solution:
Let Installment per month(P) = ₹ y
Number of months(n) = 12
Rate of interest(r) = 11% p.a.

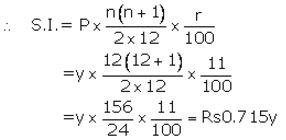
Maturity value = ₹ (y × 12) + ₹ 0.715y = ₹ 12.715y
Given maturity value = ₹ 12,715
Then ₹ 12.715y = ₹ 12,715

Question 5.
A man has a Recurring Deposit Account in a bank for 3 ½ years. If the rate of interest is 12% per annum and the man gets ₹ 10,206 on maturity, find the value of monthly instalments.
Solution:
Let Installment per month(P) = ₹ y
Number of months(n) = 42
Rate of interest(r) = 12% p.a.

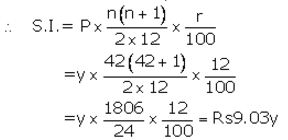
Maturity value= ₹ (y × 42) + ₹ 9.03y= ₹ 51.03y
Given maturity value = ₹ 10,206
Then ₹ 51.03y = ₹ 10206

Question 6.
(i) Puneet has a Recurring Deposit Account in the Bank of Baroda and deposits ₹ 140 per month for 4 years. If he gets ₹ 8,092 on maturity, find the rate of interest given by the bank.
(ii) David opened a Recurring Deposit Account in a bank and deposited ₹ 300 per month for two years. If he received ₹ 7,725 at the time of maturity, find the rate of interest per annum.
Solution:
(a)
Installment per month(P) = ₹ 140
Number of months(n) = 48
Let rate of interest(r) = r% p.a.

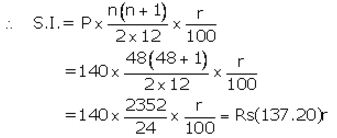
Maturity value= ₹ (140 × 48) + ₹ (137.20)r
Given maturity value = ₹ 8,092
Then ₹ (140 × 48) + ₹ (137.20)r = ₹ 8,092
⇒ 137.20r = ₹ 8,092 – ₹ 6,720

(b)
Instalment per month(P) = ₹ 300
Number of months(n) = 24
Let rate of interest(r)= r% p.a.

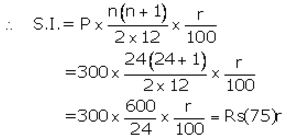
Maturity value = ₹ (300 × 24) + ₹ (75)r
Given maturity value = ₹ 7,725
Then ₹ (300 × 24) + ₹ (75)r = ₹ 7,725
⇒ 75 r = ₹ 7,725 – ₹ 7,200

Question 7.
Amit deposited ₹ 150 per month in a bank for 8 months under the Recurring Deposit Scheme. What will be the maturity value of his deposits, if the rate of interest is 8% per annum and interest is calculated at the end of every month?
Solution:
Installment per month(P) = ₹ 150
Number of months(n) = 8
Rate of interest(r) = 8% p.a.

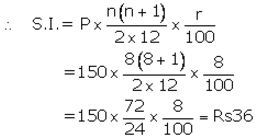
The amount that Manish will get at the time of maturity
= ₹ (150 × 8) + ₹ 36
= ₹ 1,200 + ₹ 36
= ₹ 1,236

Question 8.
Mrs. Geeta deposited ₹ 350 per month in a bank for 1 year and 3 months under the Recurring Deposit Scheme. If the maturity value of her deposits is ₹ 5,565; find the rate of interest per annum.
Solution:
Installment per month(P) = ₹ 350
Number of months(n) = 15
Let rate of interest(r)= r% p.a.

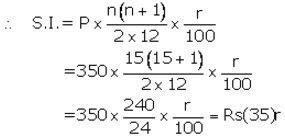
Maturity value= ₹ (350 × 15) + ₹ (35)r
Given maturity value = ₹ 5,565
Then ₹ (350 × 15) + ₹ (35)r = ₹ 5,565
⇒ 35r = ₹ 5,565 – ₹ 5,250

Question 9.
A recurring deposit account of ₹ 1,200 per month has a maturity value of ₹ 12,440. If the rate of interest is 8% and the interest is calculated at the end of every month; find the time (in months) of this Recurring Deposit Account.
Solution:
Installment per month(P) = ₹ 1,200
Number of months(n) = n
Let rate of interest(r) = 8% p.a.

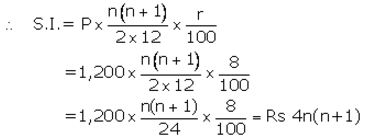
Maturity value = ₹ (1,200 × n) + ₹ 4n(n+1) = ₹ (1200n+4n²+4n)
Given maturity value= ₹ 12,440
Then 1200n+4n²+4n = 12,440

Then number of months = 10

Question 10.
Mr. Gulati has a Recurring Deposit Account of ₹ 300 per month. If the rate of interest is 12% and the maturity value of this account is ₹ 8,100; find the time (in years) of this Recurring Deposit Account.
Solution:
Installment per month(P) = ₹ 300
Number of months(n) = n
Let rate of interest(r)= 12% p.a.

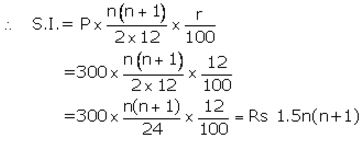
Maturity value= ₹ (300 × n)+ ₹ 1.5n(n+1)
= ₹ (300n+1.5n²+1.5n)
Given maturity value= ₹ 8,100
Then 300n+1.5n²+1.5n = 8,100

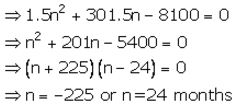
Then time = 2 years.

Question 11.
Mr. Gupta opened a recurring deposit account in a bank. He deposited ₹ 2,500 per month for two years. At the time of maturity he got ₹ 67,500. Find:
(i) the total interest earned by Mr. Gupta
(ii) the rate of interest per annum.
Solution:
(i)
Maturity value = ₹ 67,500
Money deposited = ₹ 2,500 × 24= ₹ 60,000
Then total interest earned = ₹ 67,500 – ₹ 60,000 = ₹ 7,500 Ans.
(ii)
Installment per month(P) = ₹ 2,500
Number of months(n) = 24
Let rate of interest(r)= r% p.a.

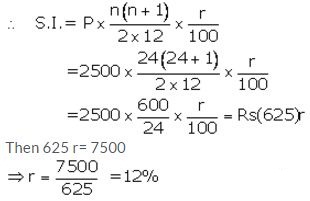
Banking (Recurring Deposit Accounts) Exercise 2B- Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.
Pramod deposits ₹ 600 per month in a Recurring Deposit Account for 4 years. If the rate of interest is 8% per year; calculate the maturity value of his account.
Solution:
Installment per month(P) = ₹ 600
Number of months(n) = 48
Rate of interest(r)= 8% p.a.

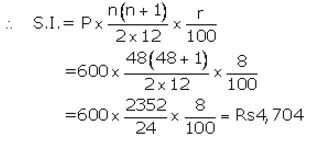
The amount that Manish will get at the time of maturity
= ₹ (600 × 48) + ₹ 4,704
= ₹ 28,800 + ₹ 4,704
= ₹ 33,504

Question 2.
Ritu has a Recurring Deposit Account in a bank and deposits ₹ 80 per month for 18 months. Find the rate of interest paid by the bank if the maturity value of account is ₹ 1,554.
Solution:
Installment per month(P) = ₹ 80
Number of months(n) = 18
Let rate of interest(r) = r% p.a.

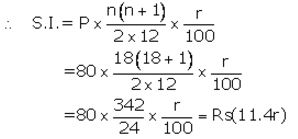
Maturity value = ₹ (80 × 18) + ₹ (11.4r)
Given maturity value = ₹ 1,554
Then ₹ (80 × 18 ) + ₹ (11.4r) = ₹ 1,554
⇒ 11.4r  = ₹ 1,554 – ₹ 1,440

Question 3.
The maturity value of a R.D. Account is ₹ 16,176. If the monthly installment is ₹ 400 and the rate of interest is 8%; find the time (period) of this R.D Account.
Solution:
Installment per month(P) = ₹ 400
Number of months(n) = n
Let rate of interest(r)= 8% p.a.


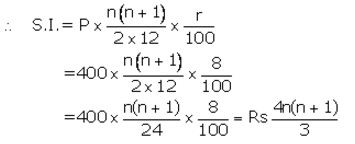
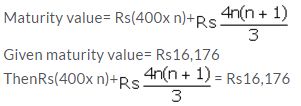
⇒ 1200n +4n²+4n= ₹ 48,528
⇒ 4n²+1204n = ₹ 48,528
⇒ n²+301n – 12132= 0
⇒ (n+337)(n-36)=0
⇒ n = -337 or n=36
Then number of months = 36 months = 3 years

Question 4.
Mr. Bajaj needs ₹ 30,000 after 2 years. What least money (in multiple of 5) must he deposit every month in a recurring deposit account to get required money after 2 years, the rate of interest being 8% p.a.?
Solution:
Let installment per month = ₹ P
Number of months(n) = 24
Rate of interest = 8% p.a.

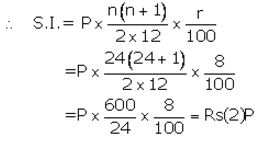
Maturity value = ₹ (P × 24)+ ₹ 2P = ₹ 26P
Given maturity value = ₹ 30,000

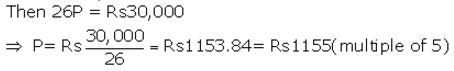
Question 5.
Rishabh has recurring deposit account in a post office for 3 years at 8% p.a. simple interest. If he gets ₹ 9,990 as interest at the time of maturity, find:
(i) The monthly installment.
(ii) The amount of maturity.
Solution:
Let Installment per month = ₹ P
Number of months(n) = 36
Rate of interest(r)= 8% p.a.

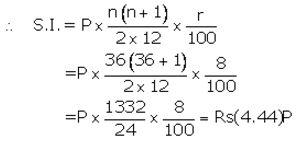
Given interest = ₹ 9,990

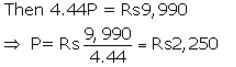
(ii) Maturity value = ₹ (2,250 × 36) + ₹ 9,990 = ₹ 90,990

Question 6.
Gopal has a cumulative deposit account and deposits ₹ 900 per month for a period of 4 years he gets ₹ 52,020 at the time of maturity, find the rate of interest.
Solution:
Installment per month(P) = ₹ 900
Number of months(n) = 48
Let rate of interest(r)= r% p.a.

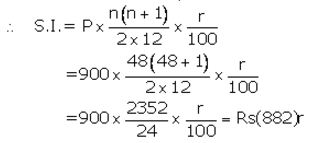
Maturity value= ₹ (900 × 48) + ₹ (882)r
Given maturity value = ₹ 52,020
Then ₹ (900 × 48) + ₹ (882)r = ₹ 52,020
⇒ 882r = ₹ 52,020 – ₹ 43,200

Question 7.
Deepa has a 4-year recurring deposit account in a bank and deposits ₹ 1,800 per month. If she gets ₹ 1,08,450 at the time of maturity, find the rate of interest.
Solution:
Installment per month(P) = ₹ 1,800
Number of months(n) = 48
Let rate of interest(r)= r% p.a.

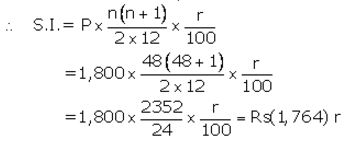
Maturity value = ₹ (1,800 x 48) + ₹ (1,764)r
Given maturity value = ₹ 1,08,450
Then ₹ (1,800 x 48) + ₹ (1764)r = ₹ 1,08,450
⇒ 1764r = ₹ 1,08,450 – ₹ 86,400

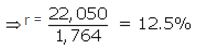
Question 8.
Mr. Britto deposits a certain sum of money each month in a Recurring Deposit Account of a bank. If the rate of interest is of 8% per annum and Mr. Britto gets Rs. 8,088 from the bank after 3 years, find the value of his monthly instalment.
Solution:

Question 9.
Shahrukh opened a Recurring Deposit Acoount in a bank and deposited Rs. 800 per month for 1 \(\frac { 1 }{ 2 }\) years. If he received Rs. 15,084 at the time of maturity, find the rate of interest per annum.
Solution:

Question 10.
Katrina opened a recurring deposit account with a Nationalised Bank for a period of 2 years. If the bank pays interest at the rate of 6% per annum and the monthly installment is ₹ 1,000, find the :
(i) interest earned in 2 years
(ii) maturity value
Solution:

Question 11.
Mohan has a recurring deposit account in a bank for 2 years at 6% p.a. simple interest. If he gets Rs. 1200 as interest at the time of maturity, find
(i) the monthly installment
(ii) the amount of maturity
Solution:
Interest, I = Rs. 1,200
Time, n = 2 years = 2 × 12 = 24 months
Rate, r = 6%
(i) To find: Monthly instalment, P
Now,

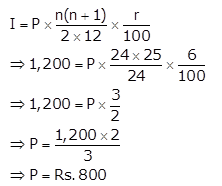
So, the monthly instalment is Rs. 800.

(ii) Total sum deposited = P × n = Rs. 800 × 24 = Rs. 19,200
∴ Amount of maturity = Total sum deposited + Interest on it
= Rs. (19,200 + 1,200)
= Rs. 20,400

Question 11.
Peter has a recurring deposit account in Punjab National Bank at Sadar Bazar, Delhi for 4 years at 10% p.a. He will get ₹ 6,370 as interest on maturity. Find :
(i) monthlyinstallment,
(ii) the maturity value of the account.
Solution:

More Resources for Selina Concise Class 10 ICSE Solutions

• Concise Mathematics Class 10 ICSE Solutions
• Concise Physics Class 10 ICSE Solutions
• Concise Chemistry Class 10 ICSE Solutions
• Concise Biology Class 10 ICSE Solutions

ICSE Solutions Selina ICSE Solutions