Selina Concise Mathematics Class 6 ICSE Solutions Chapter 20 Substitution (Including Use of Brackets as Grouping Symbols)
Selina Publishers Concise Mathematics Class 6 ICSE Solutions Chapter 20 Substitution (Including Use of Brackets as Grouping Symbols)
ICSE SolutionsSelina ICSE SolutionsML Aggarwal Solutions
APlusTopper.com provides step by step solutions for Selina Concise ICSE Solutions for Class 6 Mathematics. You can download the Selina Concise Mathematics ICSE Solutions for Class 6 with Free PDF download option. Selina Publishers Concise Mathematics for Class 6 ICSE Solutions all questions are solved and explained by expert mathematic teachers as per ICSE board guidelines.
Selina Class 6 Maths ICSE SolutionsPhysicsChemistryBiologyGeographyHistory & Civics
IMPORTANT POINTS
- Substitution : The value of an expression depends on the value of its variable (s).
- Use of Brackets :
The Symbols —, ( ), { }, [ ] are called brackets.
If an expression is enclosed within a bracket, it is considered a single quantity, even if it is made up of many terms.
Keep in Mind :- While simplifying an expression containing a bracket, first of all, the terms inside the bracket are operated (combined).
- ( ) is called a small bracket or Parenthesis.
- { } is called a middle bracket or Curly bracket.
- [ ] is called big or square bracket.
- If one more bracket is needed, then we use the bar bracket.
i.e. a line ———— is drawn over a group of terms.
Thus, in \(3x+\bar { 4y-5z }\), the line over 4y – 5z serves as the bar bracket and is called Vinculum.
Substitution Exercise 20A – Selina Concise Mathematics Class 6 ICSE Solutions
Question 1.
Fill in the following blanks, when :
x = 3,y = 6, z = 18, a = 2, b = 8, c = 32 and d = 0.
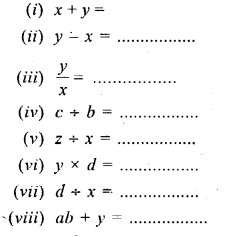
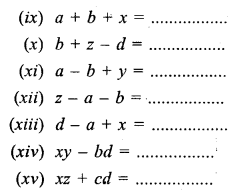
Solution:
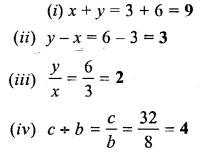
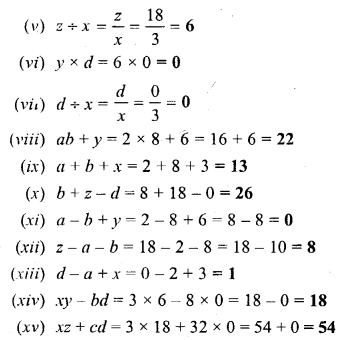
Question 2.
Find the value of :
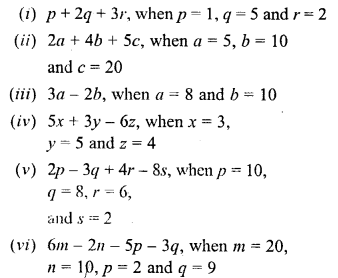
Solution:
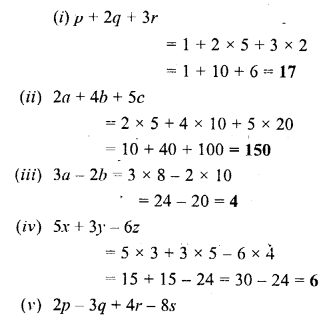
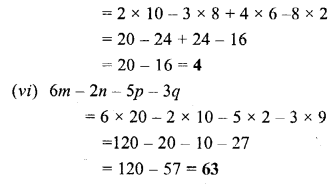
Question 3.
Find the value of :
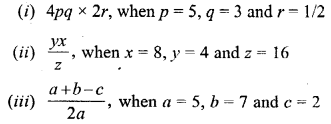
Solution:
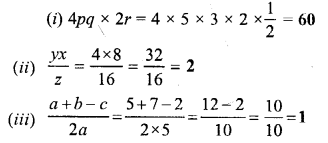
Question 4.
If a = 3, b = 0, c = 2 and d = 1, find the value of :
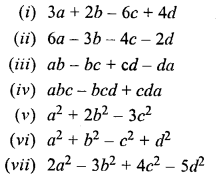
Solution:
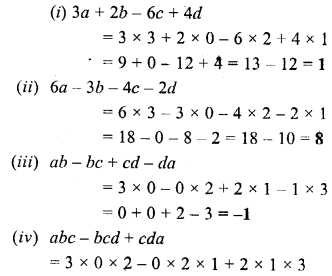
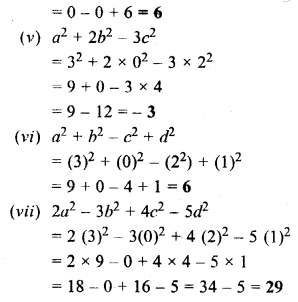
Question 5.
Find the value of 5x2 – 3x + 2, when x = 2.
Solution:
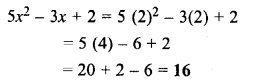
Question 6.
Find the value of 3x3 – 4x2 + 5x – 6, when x = -1.
Solution:
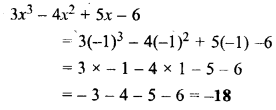
Question 7.
Show that the value of x3 – 8x2 + 12x – 5 is zero, when x = 1.
Solution:
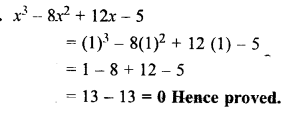
Question 8.
State true and false :
(i) The value of x + 5 = 6, when x = 1
(ii) The value of 2x – 3 = 1, when x = 0
(iii) \(\frac { 2x-4 }{ x+1 }\) = -1,when x = 1
Solution:

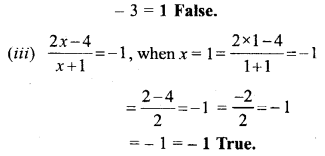
Question 9.
If x = 2, y = 5 and z = 4, find the value of each of the following :
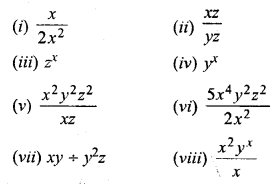
Solution:
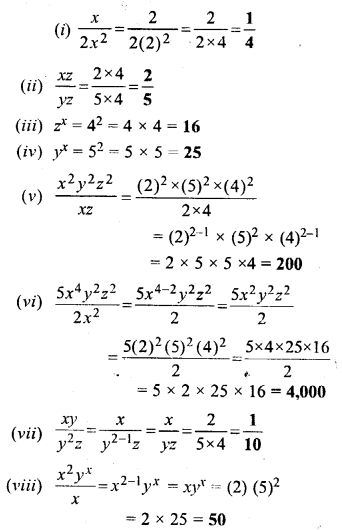
Question 10.
If a = 3, find the values of a2 and 2a.
Solution:
a2 = (3)2 = 3 x 3 = 9
2a = (2)3 = 2 x 2 x 2 = 8
Question 11.
If m = 2, find the difference between the values of 4m3 and 3m4.
Solution:
4m3 = 4 (2)3 = 4 x 2 x 2 x 2 = 32
3m4 = 3 (2)4 = 3 x 2 x 2 x 2 x 2 = 48
Now, a difference 3m4 – 4m3 = 48 – 32 = 16
Substitution Exercise 20B – Selina Concise Mathematics Class 6 ICSE Solutions
Question 1.
Evaluate :
(i) (23 – 15) + 4
(ii) 5x + (3x + 7x)
(iii) 6m – (4m – m)
(iv) (9a – 3a) + 4a
(v) 35b – (16b + 9b)
(vi) (3y + 8y) – 5y
Solution:
(i) (23 – 15) + 4 = 8 + 4 = 12
(ii) 5x + (3x + 7x) = 5x + 10x = 15x
(iii) 6m – (4m – m) = 6m – 3m = 3m
(iv) (9a – 3a) + 4a = 6a + 4a = 10a
(v) 35b – (16b + 9b)= 35b – 25b = 10b
(vi) (3y + 8y) – 5y = 11y – 5y = 6y
Question 2.
Simplify :
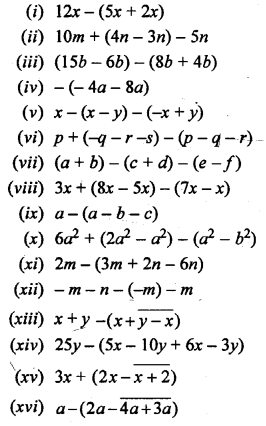
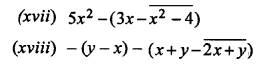
Solution:
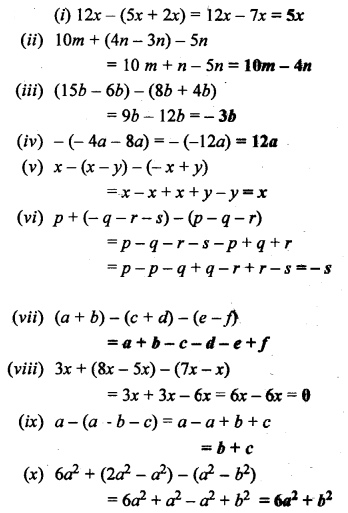
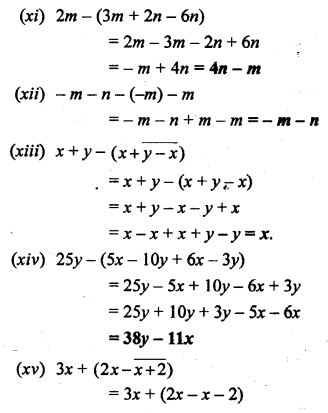
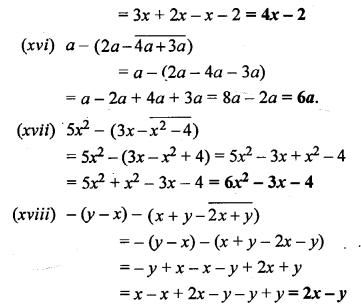
Question 3.
Simplify :
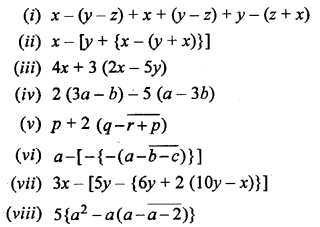
Solution:
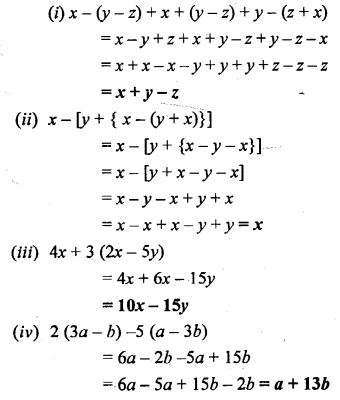
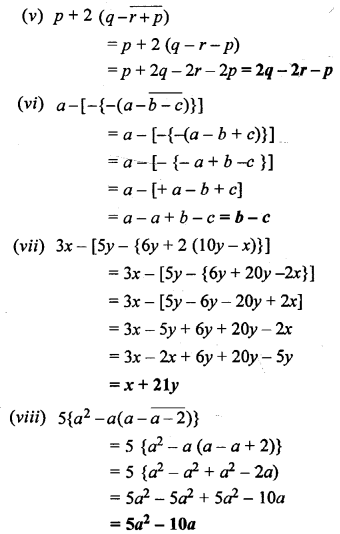
Substitution Exercise 20C – Selina Concise Mathematics Class 6 ICSE Solutions
Question 1.
Fill in the blanks :
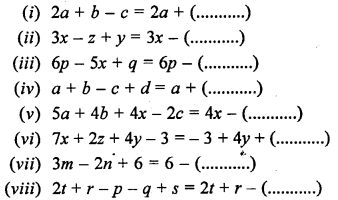
Solution:
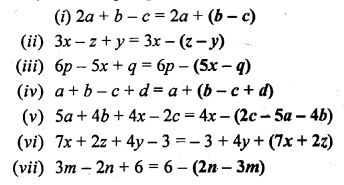
(viii) 2t + r – p – q + s = 2t + r – (p + q – s)
Question 2.
Insert the bracket as indicated :
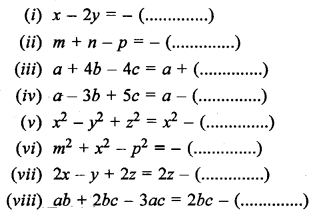
Solution:
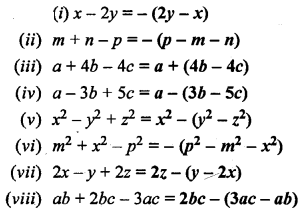
Substitution Revision Exercise – Selina Concise Mathematics Class 6 ICSE Solutions
Question 1.
Find the value of 3ab + 10bc – 2abc when a = 2, b = 5 and c = 8.
Solution:
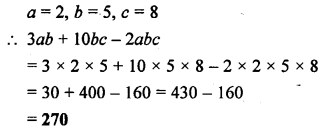
Question 2.
If x = 2, = 3 and z = 4, find the value of 3x2 – 4y2 + 2z2.
Solution:
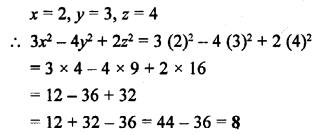
Question 3.
If x = 3, y = 2 and z = 1; find the value of:
(i) xy
(ii) yx
(iii) 3x2 – 5y2
(iv) 2x – 3y + 4z + 5
(v) y2 – x2 + 6z2
(vi) xy + y2z – 4zx
Solution:
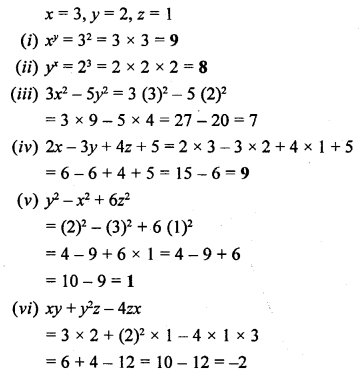
Question 4.
If P = -12x2 – 10xy + 5y2, Q = 7x2 + 6xy + 2y2, and R = 5x2 + 2xy + 4y2 ; find :
(i) P – Q
(ii) Q + P
(iii) P – Q + R
(iv) P + Q + R
Solution:
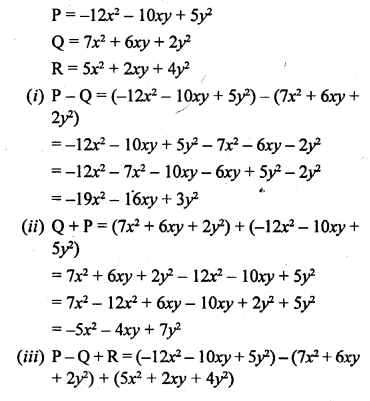
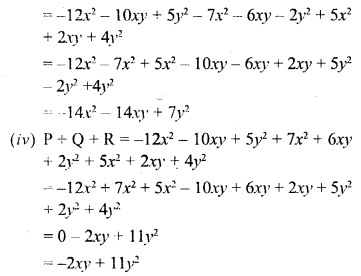
Question 5.
If x = a2 – bc, y = b2 – ca and z = c2 – ab ; find the value of :
(i) ax + by + cz
(ii) ay – bx + cz
Solution:
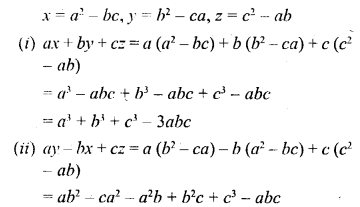
Question 6.
Multiply and then evaluate :
(i) (4x + y) and (x – 2y); when x = 2 and y = 1.
(ii) (x2 – y) and (xy – y2); when x = 1 and y = 2.
(iii) (x – 2y + z) and (x – 3z); when x = -2, y = -1 and z = 1.
Solution:
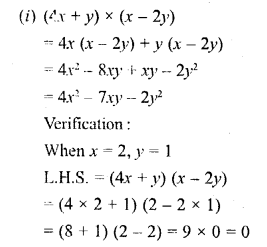

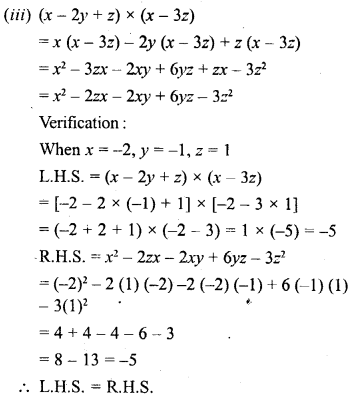
Question 7.
Simplify :
(i) 5 (x + 3y) – 2 (3x – 4y)
(ii) 3x – 8 (5x – 10)
(iii) 6 {3x – 8 (5x – 10)}
(iv) 3x – 6 {3x – 8 (5x – 10)}
(v) 2 (3x2 – 4x – 8) – (3 – 5x – 2x2)
(vi) 8x – (3x – \(\bar { 2x-3 }\))
(vii) 12x2 – (7x – \(\bar { 3x^{ 2 }+15 }\))
Solution:
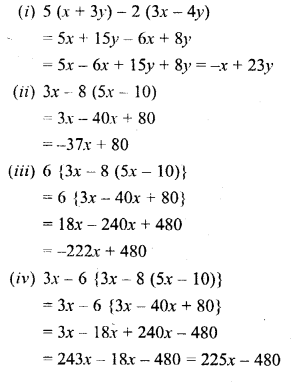
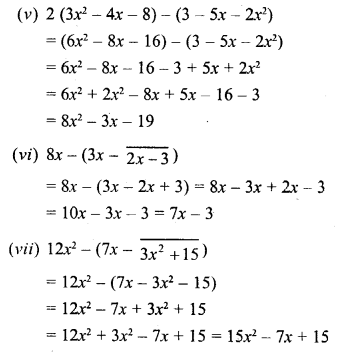
Question 8.
If x = -3, find the value of : 2x3 + 8x2 – 15.
Solution:
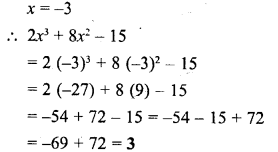
Selina Class 6 Maths ICSE SolutionsPhysicsChemistryBiologyGeographyHistory & Civics