Selina Concise Mathematics Class 6 ICSE Solutions Chapter 10 Sets

Selina Publishers Concise Mathematics Class 6 ICSE Solutions Chapter 10 Sets

ICSE Solutions Selina ICSE Solutions ML Aggarwal Solutions

APlusTopper.com provides step by step solutions for Selina Concise ICSE Solutions for Class 6 Mathematics. You can download the Selina Concise Mathematics ICSE Solutions for Class 6 with Free PDF download option. Selina Publishers Concise Mathematics for Class 6 ICSE Solutions all questions are solved and explained by expert mathematic teachers as per ICSE board guidelines.

Selina Class 6 Maths ICSE Solutions Physics Chemistry Biology Geography History & Civics

IMPORTANT POINTS

In our day-to-day life we often speak or hear about different types of collections.
Such as :
(i) A collection of stamps.
(ii) A collection of toys :
(iii) A collection of books, etc.
In the same way, we have different types of groups made for different activities.
Such as :
(i) A group of boys playing hockey.
(ii) A group of girls playing badminton.
(iii) A group of students going for picnic, etc.
In mathematics, a collection of particular things or a group of particular objects is called a set.

Definition of a Set : A set is a collection of well-defined objects.
Meaning of “Well-Defined” : Well- defined means, it must be absolutely clear that which object belongs to the set and which does not.
Elements (or, members) of a set : The objects used to form a set are called its elements or its members.
Keep in Mind :
- The pair of curly braces { } denotes a set.
- The Greek letter Epsilon ‘ ε ’ is used for the words “belongs to”, “is an element of, etc.
  p ε A will be be read as “p belongs to set A” or “p is an element of set A”.
  In the same way ; q ε A, r ε A, s ε a. and t ε A.
  The symbol ‘ε not’ stands for “does not belong to” also for “is not an element of.
  a ε not A will be read as “a does not belong to set A” or “a is not an element of set A”.
Properties of a set :
- The change in order of writing the elements does not make any change in the set.
- If one or many elements of a set are repeated, the set remains the same.
Notation (Representation) of a set :
- Description method : In this method, a well-defined description about the elements of the set is made.
- Roster or Tabular Method : In this method, the elements (members) of a set are written inside a pair of curly braces and are separated by commas.
- Rule or Set Builder Method : In this method, actual elements of the set are not listed but a rule or a statement or a formula, in the briefest possible way, is written inside a pair of curly braces.

Sets Exercise 10A – Selina Concise Mathematics Class 6 ICSE Solutions

Question 1.
State whether or not the following elements form a set; if not, give reason:
(i) All easy problems in your text book.
(ii) All three sided figures.
(iii) The first five counting numbers.
(iv) All the tall boys of your class.
(v) The last three days of the week.
(vi) All triangles that are difficult to draw.
(vii) The first three letters of the English alphabet.
(viii) All tasty fruits.
(ix) All clever boys of class 6.
(x) All good schools in Delhi.
(xi) All the girls in your class, whose heights are less than your height.
(xii) All the boys in your class, whose heights are more than your height.
(xiii) All the problems in your Mathematics book, which are difficult for Amit.
Solution:
(i) No; some problems may be easy for one person but may be difficult to some other person. Objects are not well- defined.
(ii) Yes.
(iii) Yes.
(iv) No; it is not mentioned that the boys must be taller than which boy. If we consider three boys A, B and C; boy B can be taller than A but not necessarily taller than C.
(v) Yes
(vi) No; it may be difficult for one boy to draw a given triangle but to some other boy it may be easy to draw the same triangle.
(vii) Yes
(viii) No; a fruit may be tasty for one person and may not be tasty to other person / persons.
(ix) No; clever in what respect and from whom out of six ?
(x) No; all the people can not find the same schools as good as others said. So, the objects are not well-defined.
(xi) Yes
(xii) Yes
(xiii) Yes.

Sets Exercise 10B – Selina Concise Mathematics Class 6 ICSE Solutions

Question 1.
If set A = {2, 3, 4, 5, 6}, state which of the following statements arc true and which are false :
(i) 2 ∈ A
(ii) 5, 6 ∈ A
(iii) 3, 4, 7 ∈ A
(iv) 2, 8 ∈ A
Solution:
(i) True
(ii) True
(iii) False
(iv) False

Question 2.
If set B = {4, 6, 8, 10, 12, 14}. State, which of the following statements is correct and which is wrong :
(i) 5 ∈ B
(ii) 12 ∈ B
(iii) 14 ∈ B
(iv) 9 ∈ B
(v) B is a set of even numbers between 2 and 16.
(vi) 4,6 and 10 are die members of the set B. Also, write the wrong statements correctly.
Solution:
(i) Wrong ; 5 \(\notin \) B
(ii) Correct
(iii) Correct
(iv) Wrong ; 9 \(\notin \) B
(v) Correct
(vi) Correct.

Question 3.
State, whether true or false :
(i) Sets {4, 9, 6,2} and {6, 2, 4, 9} are not the same.
(ii) Sets {0, 1, 3, 9, 4} and {4, 0, 1, 3, 9} are the same.
(iii) Sets {5, 4} and {5, 4, 4, 5} are not the same.
(iv) Sets {8, 3} and {3, 3, 8} are the same.
(v) Collection of vowels used in the word ‘ALLAHABAD’ forms a set.
(vi) If P is the set of letters in the word ‘ROOP’; then P = (p, o, r)
(vii) If M is the set of letters used in the word ‘MUMBAI’, then: M = {m, u, b, a, i}
Solution:
(i) False.
(ii) True.
(iii) False.
(iv) True.
(v) True.
(vi) True.
(vii) True.

Question 4.
Write the set containing :
(i) the first five counting numbers.
(ii) the three types of angles.
(iii) the three types of triangles.
(iv) the members of your family.
(v) the first six consonants of the English Alphabet.
(vi) the first four vOWels of the English Alphabet.
(vii) the names of any three Prime-Ministers of India.
Solution:
(i) {1, 2, 3, 4, 5}
(ii) {acute-angle, obtuse-angle, right-angle}.
(iii) {scalene triangle, isosceles triangles, equilateral triangle}.
(iv) { Write the name of family member}.
(v) {b, c, d, f, g, h}
(vi) {a, e, i, o}
(vii) {J.L. Nehru, A.B. Vajpayee, Dr. Manmohan Singh}.

Question 5.
(a) Write the members (elements) of each set given below :
(i) {3, 8, 5, 15, 12, 7}
(ii) {c, m, n, o, s}
(b) Write the sets whose elements are :
(i) 2, 4, 8, 16, 64 and 128
(ii) 3, 5, 15, 45, 75 and 90
Solution:
(a) (i) 3, 8, 5, 15, 12 and 7
(ii) c, m, n, o and s
(b) (i) {2, 4, 8, 16, 64, 128}
(ii) {3, 5, 15, 45, 75, 90}

Question 6.
(i) Write the set of letters used in the word ‘BHOPAL’.
(ii) Write the set of vowels used im the word ‘BENGAL’.
(iii) Write the set of consonants used in the word ‘HONG KONG’.
Solution:
(i) {b, h, o, p, a, 1}
(ii) {e, a}
(iii) {h, o, n, g, k}

Sets Exercise 10C – Selina Concise Mathematics Class 6 ICSE Solutions

Question 1.
Write each of the following sets in the Roster Form :
(i) The set of five numbers each of which is divisible by 3.
(ii) The set of integers between – 4 and 4.
(iii) {x: x is a letter in the word ‘ SCHOOL’}
(iv) {x: x is an odd natural number between 10 and 20}
(v) {Vowels used in the word ‘AMERICA’}
(vi) {Consonants used in the * word ‘MADRAS’}
Solution:
(i) {3, 6, 9, 12, 15}
(ii) {-3, -2, -1, 0, 1, 2, 3}
(iii) {s, c, h, o, 1}
(iv) {11, 13, 15, 17, 19}
(v) (a, e, i)
(vi) {m, d, r, s}

Question 2.
Write each given set in the Roster Form :
(i) All prime numbers between one and twenty.
(ii) The squares of first four natural numbers.
(iii) Even numbers between 1 and 9.
(iv) First eight letters of the English alphabet.
(v) The letters of the word ‘BASKET’.
(vi) Four cities of India whose names start with the letter J.
(vii) Any four closed geometrical figures.
(viii) Vowels used in the word ‘MONDAY’.
(ix) Single digit numbers that are perfect squares as well.
Solution:
(i) {2, 3, 5, 7, 11, 13, 17, 19}
(ii) {12, 22, 32, 42} = {1, 4, 9, 16}
(iii) {2, 4, 6, 8}
(iv) {a, b, c, d, e, f, g, h}
(v) {b, a, s, k, e, t}
(vi) {Jaipur, Jodhpur, Jalandhar, Jaunpur}
(vii) {∆, O, □, O}
(viii) {o, a}
(ix) {0, 1, 4, 9}

Question 3.
Write each given set in the Set- Builder Form :
(i) {2, 4, 6, 8, 10}
(ii) {2, 3, 5, 7, 11}
(iii) {January, June, July}
(iv) {a, e, i, o, u}
(v) {Tuesday, Thursday}
(vi) {1,4,9, 16, 25}
(vii) {5,10,15,20,25,30}
Solution:
(i) {x : x is an even natural number less than 12}
(ii) {x : x is a prime number less than 12}
(iii) {x : x is a months of the year whose name starts with letter J}
(iv) {x : x is a vowel in English alphabets}
(v) {x : x is a day of the week whose name starts with letter T}
(vi) {x: x is a perfect square natural number upto 25}
(vii) {x : x is a natural number upto 30 and divisible by 5}.

Question 4.
Write each of the following sets in Roster (tabular) Form and also in Set-Builder Form.
(i) Set of all natural numbers that can divide 24 completely.
(ii) Set of odd numbers between 20 and 35.
(iii) Set of letters used in the word ‘CALCUTTA’.
(iv) Set of names of the first five months of a year.
(v) Set of all two digit numbers that are perfect square as well.
Solution:
(i) {1,-2, 3, 4, 6, 8, 12, 24}; {x : x is a natural number which divides 24 completely}
(ii) {21, 23, 25, 27, 29, 31, 33}; {x:x is an odd number between 20 and 35}
(iii) {c, a, 1, u, t}; {x: x is a letter used in the word ‘CALCUTTA’}
(iv) {January, February, March,April, May}; {x : x is name of first five months of a year}
(v) {16, 25, 36, 49, 64, 81}; {x : x is a perfect square two digit number}.

Question 5.
Write, in Roster Form, the set of :
(i) the first four odd natural numbers each divisible by 5.
(ii) th counting numbers between 15 and 35; each of which is divisible by 6.
(iii) the names of the last three days of a week.
(iv) the names of the last four months of a year.
Solution:
(i) {5, 15, 25, 35}
(ii) {18, 24, 30}
(iii) {Friday, Saturday, Sunday}
(iv) {September, October, November, December}.

Sets Exercise 10D – Selina Concise Mathematics Class 6 ICSE Solutions

Question 1.
State, whether the given set is infinite or finite :
(i) {3, 5, 7, ………}
(ii) {1, 2, 3, 4}
(iii) {………., -3, -2, -1, 0, 1, 2}
(iv) {20, 30, 40, 50, …, 200}
(v) {7, 14, 21, ……….., 2401}
Solution:
(i) Infinite
(ii) Finite
(iii) Infinite
(iv) Finite
(v) Finite

Question 2.
(i) Which of the following sets is empty ?
(ii) Set of counting numbers between 5 and 6.
(iii) Set of odd numbers between 7 and 19. Set of odd numbers between 7 and 9.
(iv) Set of even numbers which are not divisible by 2.
(v) {0}.
Solution:
(i), (iii) and (iv)

Question 3.
State, which pair of sets, given below, are equal sets or equivalent sets:
(i) {3, 5, 7} and {5, 3, 7}
(ii) {8, 6, 10, 12} and {3, 2, 4, 6}
(iii) {7, 7, 2, 1,2} and {1, 2, 7}
(iv) {2, 4, 6, 8, 10} and {a, b, d, e, m}
(v) {5, 5, 2, 4} and {5, 4, 2, 2}
Solution:
(i) Equal
(ii) Equivalent
(iii) Equal
(iv) Equivalent
(v) Equal

Question 4.
State, which of the following are finite or infinite sets :
(i) Set of integers
(ii) {Multiples of 5}
(iii) {Fractions between 1 and 2}
(iv) {Number of people in India}
(v) Set of trees in the world
(vi) Set of leaves on a tree
(vii) Set of children in all the schools of Delhi
(viii) { …….., -4, -2, 0, 2, 4, 6, 8}
(ix) {- 12, – 9, – 6, – 3, 0, 3, 6, …….}
(x) {Number of points in a line segment 4 cm long}.
Solution:
(i) Infinite
(ii) Infinite
(iii) Infinite
(iv) Finite
(v) Infinite
(vi) Finite
(vii) Finite
(viii) Infinite
(ix) Infinite
(x) Infinite

Question 5.
State, whether or not the following sets are empty :
(i) {Prime numbers divisible by 2}
(ii) {Negative natural numbers}
(iii) {Women with height 5 metre}
(iv) {Integers less than 5}
(v) {Prime numbers between 17 and 23}
(vi) Set of even numbers, not divisible by 2
(vii) Set of multiples of 3, which are more than 9 and less than 15.
Solution:
(i) Not empty
(ii) Empty
(iii) Empty
(iv) Not empty
(v) Not empty
(vi) Empty
(vii) Not empty

Question 6.
State, if the given pairs of sets are equal sets or equivalent sets :
(i) {Natural numbers less than five} and {Letters of the word ‘BOAT’}.
(ii) {2, 4, 6, 8, 10} and {even natural numbers less than 12}
(iii) {1, 3, 5, 7, ………..} and set of odd natural numbers.
(iv) {Letters of the word MEMBER} and {Letters of the word ‘REMEMBER’}.
(v) {Negative natural numbers} and {50th day of a month}
(vi) {Even natural numbers} and {odd natural numbers}.
Solution:
(i) Equivalent
(ii) Equal
(iii) Equal
(iv) Equal
(v) Equal
(vi) Equivalent

Question 7.
State, whether the following are finite or infinite sets :
(i) {2, 4, 6, 8, …… 800}
(ii) {……, -5, -4, -3, -2}
(iii) {x : x is an integer between – 60 and 60}
(iv) {No. of electrical appliances working in your house}
(v) {x : x is a whole number greater than 20}
(vi) {x : x is a whole number less than 20}
Solution:
(i) Finite
(ii) Infinite
(iii) Finite
(iv) Finite
(v) Infinite
(vi) Finite

Question 8.
For each statement, given below, write True or False :
(i) {…., -8, -4, 0, 4, 8} is a finite set.
(ii) { – 32, – 28, – 24, – 20, ……….. , 0, 4, 8, 16} is an infinite set.
(iii) {x : x is a natural number less than 1} is the empty set.
(iv) {Whole numbers between 15 and 16} = {Natural numbers between 5 and 6}
(v) {Odd numbers divisible by 2} is the empty set.
(vi) {Even natural numbers divisible by 3} is the empty set.
(vii) {x : x is positive and x < 0} is the empty set.
(viii) {.., -5, -3, -1, 1, 3, 5, ..} is a finite set.
Solution:
(i) False
(ii) False
(iii) True
(iv) True (each set is the empty set)
(v) True
(vi) False (6 is an even natural number which is divisible by 3)
(vii) True (no positive number can be less than 0)
(viii) False

Question 9.
State, giving reasons, which of the following pairs of sets are disjoint sets and which are or overlapping sets :
(i) A = {Girls with ages below 15 years} and B = {Girls with ages above 15 years}
(ii) C = {Boys with ages above 20 years} and D = {Boys with ages above 27 years}
(iii) A = {Natural numbers between 35 and 60} and B = {Natural numbers between 50 and 80}
(iv) P = {Students of class IX studying in I.C.S.E. Board} and Q = {Students of class IX}
(v) A = {Natural numbers multiples of 3 and less than 30} and B = {Natural numbers divisible by 4 and between 20 and 45}
(vi) P = {Letters in the word ‘ALLAHABAD’} and Q = {Letters in the word ‘MUSSOORIE’}
Solution:
(i) Disjoint sets; as no girl can be of age below 15 years and also above 15 years
(ii) Overlapping sets; as boys above 27 years are also above 20 years.
(iii) Overlapping sets; as natural numbers from 50 to 59 are common to both the sets.
(iv) Overlapping sets; as students of class IX studying in I,C.S.E. board are common.
(v) Overlapping sets; as natural number 24 is common to both the sets.
(vi) Disjoint sets; as no letter is common to both the sets.

Sets Exercise 10E – Selina Concise Mathematics Class 6 ICSE Solutions

Question 1.
Write the cardinal number of each of the following sets :
(i) A = {0, 1, 2, 4}
(ii) B = {-3, -1, 1, 3, 5, 7}
(iii) C = { }
(iv) D= {3, 2, 2, 1, 3, 1, 2}
(v) E = {Natural numbers between 15 and 20}
(vi) F = {Whole numbers from 8 to 14}.
Solution:
(i) A = {0, 1, 2, 4} i.e. n (A) = 4
(ii) B = {-3, -1, 1, 3, 5, 7} i.e. n(B) = 6
(iii) C = { } i.e. n(C) = 0
(iv) D = {3, 2, 2, 1,3, 1, 2} => D = {3, 2, 1,} i.e. n(D) = 3
(v) E = {16, 17, 18 19} i.e. n(E) = 4
(vi) F={8, 9, 10, 11, 12, 13, 14} i.e. n(F) = 7

Question 2.
Given :
(i) A = {Natural numbers less than 10}
B = {Letters of the word ‘PUPPET’}
C = {Squares of first four whole numbers}
D = {Odd numbers divisible by 2}. Find :
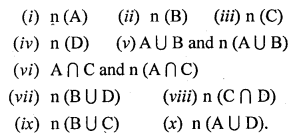
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 10 Sets image - 1
Solution:

Question 3.
State true or false for each of the following. Correct the wrong statement.
(i) If A = {0}, then n(A) = 0.
(ii) n(φ) = 1.
(iii) If T ={a, l, a, h, b, d, h), then n(T) = 5.
(iv) If B ={1, 5, 51, 15, 5, l},then n(B) = 6.
Solution:
(i) A = {0} then n(A) = 0 which is false.
True statement is n (A) = 1
(ii) n(φ) = 1, which is false.
i.e. n (φ) = 0
(iii) T = {a, l, a, h, b, d, h} i.e. T = {a, l, h, b, d)
i.e. n(T) = 5 which is true.
(iv) B = {1, 5, 51, 15, 5, 1} n(B) = 6 which is false.
i.e. B = {1, 5, 51, 15} => n(B) = 4

Selina Class 6 Maths ICSE Solutions Physics Chemistry Biology Geography History & Civics