Selina Concise Mathematics Class 6 ICSE Solutions Chapter 28 Polygons

Selina Concise Mathematics Class 6 ICSE Solutions Chapter 28 Polygons

Selina Publishers Concise Mathematics Class 6 ICSE Solutions Chapter 28 Polygons

ICSE SolutionsSelina ICSE SolutionsML Aggarwal Solutions

APlusTopper.com provides step by step solutions for Selina Concise ICSE Solutions for Class 6 Mathematics. You can download the Selina Concise Mathematics ICSE Solutions for Class 6 with Free PDF download option. Selina Publishers Concise Mathematics for Class 6 ICSE Solutions all questions are solved and explained by expert mathematic teachers as per ICSE board guidelines.

Selina Class 6 Maths ICSE SolutionsPhysicsChemistryBiologyGeographyHistory & Civics

IMPORTANT POINTS

1. Polygon : A closed plane geometrical figure, bounded by atleast three line segments, is called a
polygon.
The adjoining figure is a polygon as it is :

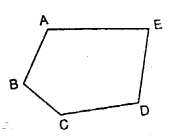
(i) Closed
(ii) bounded by five line segments AB, BC, CD, DE and AE.
Also, it is clear from the given polygon that:
(i) the line segments AB, BC, CD, DE and AE intersect at their end points.
(ii) two line segments, with a common vertex, are not collinear i.e. the angle at any vertex is not 180°.
A polygon is named according to the number of sides (line-segments) in it:

2. Sum of Interior Angles of a Polygon
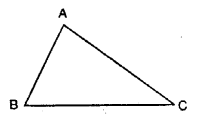
1. Triangle : Students already know that the sum of interior angles of a triangle is always 180°.
i.e. for ∆ ABC, ∠B AC + ∠ABC + ∠ACB = 180°
⇒ ZA + ZB + ZC = 180°

2. Quadrilateral : Consider a quadrilateral ABCD as shown alongside.
If diagonal AC of the quadrilaterals drawn, the quadrilateral will be divided into two triangles ABC and ADC.
Since, the sum of interior angles of a triangle is 180°.

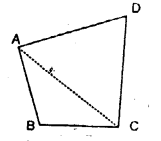
∴ In ∆ ABC, ∠ABC + ∠BAC +∠ACB = 180°
And, in ∆ ADC ∠DAC + ∠ADC + ∠ACD = 180°
Adding we get:
∠ABC + ∠BAC +∠ACB + ∠DAC + ∠ADC + ∠ACD = 180° +180°
⇒(∠BAC + ∠DAC) + ∠ABC + (∠ACB + ∠ACD) + ∠ADC = 360°
⇒∠BAD + ∠ABC + ∠BCD + ∠ADC = 360°
⇒ ∠A + ∠B + ∠C + ∠D = 360°
Alternative method : On drawing the diagonal AC, the given quadrilateral is divided into two triangles. And, we know the sum of the interior angles of a triangle is 180°.
∴ Sum of interior angles of the quadrilateral ABCD
= Sum of interior angles of ∆ ABC + sum of interior angles of ∆ ADC = 180°+ 180° = 360°

3. Pentagon : Consider a pentagon ABCDE as shown alongside.
On joining CA and CE, the given pentagon is divided into three triangles ABC, CDE and ACE.

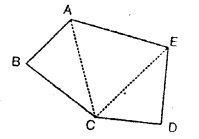
Since, the sum of the interior angles of a triangle is 180°
Sum of the interior angles of the pentagon ABCDE = Sum of interior angles of (∆ ABC + ∆ CDE + ∆ACE)
= 180° + 180° + 180° = 540°

4. Hexagon :
It is clear from the given figure that the sum of the interior angles of the hexagon ABCDEF.

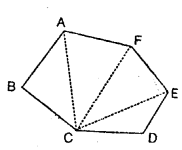
= Sum of inteior angles of
(∆ABC + ∆ ACF + ∆ FCE + ∆ ECD)
= 180° + 180° + 180° + 180° = 720°

3. Using Formula : The sum of interior angles of a polygon can also be obtained by using the following formula:
Note : Sum of interior angles of a polygon = (n – 2) x 180°
where, n = number of sides of the polygon.

Polygons Exercise 28A – Selina Concise Mathematics Class 6 ICSE Solutions

Question 1.
State, which of the following are polygons :

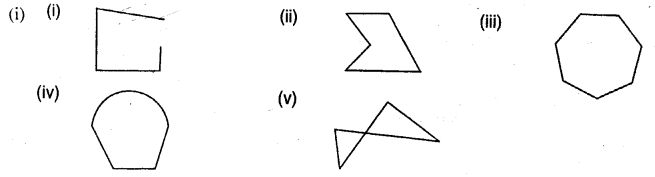
Solution:
Only figure (ii) and (iii) are polygons.

Question 2.
Find the sum of interior angles of a polygon with :
(i) 9 sides
(ii) 13 sides
(iii) 16 sides
Solution:
(i) 9 sides
No. of sides n = 9
∴Sum of interior angles of polygon = (2n – 4) x 90°
= (2 x 9 – 4) x 90°
= 14 x 90°= 1260°
(ii) 13 sides
No. of sides n = 13
∴ Sum of interior angles of polygon = (2n – 4) x 90° = (2 x 13 – 4) x 90° = 1980°
(iii) 16 sides
No. of sides n = 16
∴ Sum of interior angles of polygon = (2n – 4) x 90°
= (2 x 16 – 4) x 90°
= (32 – 4) x 90° = 28 x 90°
= 2520°

Question 3.
Find the number of sides of a polygon, if the sum of its interior angles is :
(i) 1440°
(ii) 1620°
Solution:

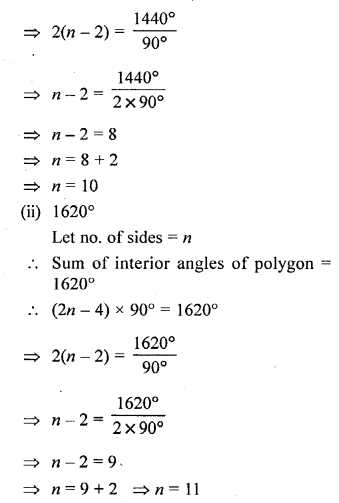
Question 4.
Is it possible to have a polygon, whose sum of interior angles is 1030°.
Solution:

Question 5.
(i) If all the angles of a hexagon arc equal, find the measure of each angle.
(ii) If all the angles of an octagon are equal, find the measure of each angle,
Solution:

Question 6.
One angle of a quadrilateral is 90° and all other angles are equal ; find each equal angle.
Solution:

Question 7.
If angles of quadrilateral are in the ratio 4 : 5 : 3 : 6 ; find each angle of the quadrilateral.
Solution:

Question 8.
If one angle of a pentagon is 120° and each of the remaining four angles is x°, find the magnitude of x.
Solution:
One angle of a pentagon = 120°
Let remaining four angles be x, x, x and x
Their sum = 4x + 120°
But sum of all the interior angles of a pentagon = (2n – 4) x 90°
= (2 x 5 – 4) x 90° = 540°
= 3 x 180° = 540°
∴ 4x+120o° = 540°
4x = 540° – 120°
4x = 420
x = \(\frac { 420 }{ 4 }\) ⇒ x = 105°
∴Equal angles are 105° (Each)

Question 9.
The angles of a pentagon are in the ratio 5 : 4 : 5 : 7 : 6 ; find each angle of the pentagon.
Solution:

Question 10.
Two angles of a hexagon are 90° and 110°. If the remaining four angles arc equal, find each equal angle.
Solution:

Polygons Exercise 28B – Selina Concise Mathematics Class 6 ICSE Solutions

Question 1.
Fill in the blanks :
In case of regular polygon, with

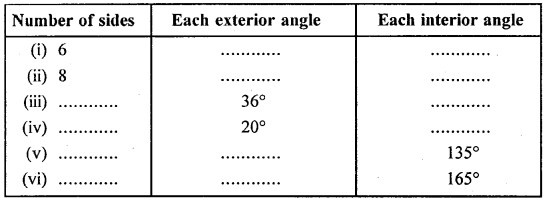
Solution:

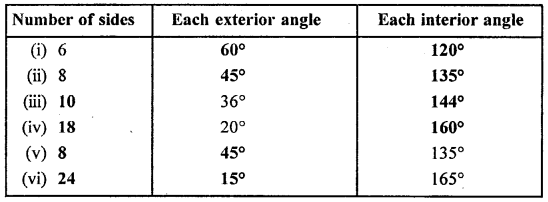
Question 2.
Find the number of sides in a regular polygon, if its each interior angle is :
(i) 160°
(ii) 150°
Solution:

Question 3.
Find number of sides in a regular polygon, if its each exterior angle is :
(i) 30°
(ii) 36°
Solution:

Question 4.
Is it possible to have a regular polygon whose each interior angle is :
(i) 135°
(ii) 155°
Solution:

Question 5.
Is it possible to have a regular polygon whose each exterior angle is :
(i) 100°
(ii) 36°
Solution:

Question 6.
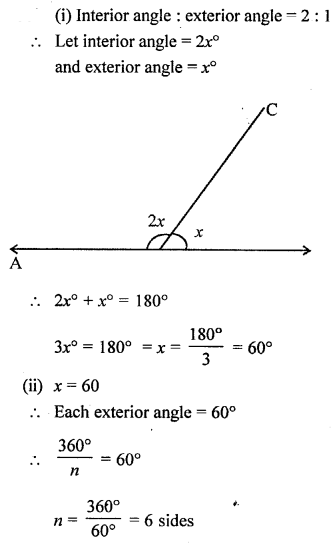
The ratio between the interior angle and the exterior angle of a regular polygon is 2 : 1. Find :
(i) each exterior angle of this polygon.
(ii) number of sides in the polygon.
Solution: