Selina Concise Mathematics Class 10 ICSE Solutions Mixed Practice Set A
Question 1.
A shokeeper buys an article for ₹ 10,800 at 10% discount on the marked price. The shopkeeper increases the marked price of the article by 15% and then sells it for ₹ 14,628 including sales tax. If the sales tax at each stage is the same, find :
(i) the rate of sales tax.
(ii) the profit percent made by the shopkeeper.
(iii) the amount of VAT paid by the shopkeeper.
Solution:
In the first case,
Cost price for the shopkeeper or sale price of the whole seller = ₹ 10800
Rate of discount = 10%
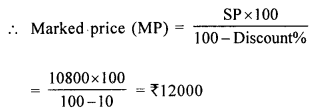
Now increase in M.P. by the shopkeeper = 15%
∴ Increase marked price
= ₹ \(\frac{12000 \times(100+15)}{100}\) = ₹ 13800
(i) Selling price = ₹ 14628
∴ Amount of sales tax = ₹ 14628 – 13800 = ₹ 828
∴ Rate of sales tax = \(\frac{828 \times 100}{13800}=6 \%\)
(ii) Now S. P. = ₹ 13800
and C. P. = ₹ 10800
∴ Total gain = S. P. – C. P.
= ₹ 13800 – 10800 = ₹ 3000
Gain%= \(\frac{\text { Total gain } \times 100}{\mathrm{CP}}\)
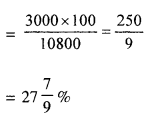
(iii) Since rate of sales tax are same
∴ Amount of VAT paid by the shopkeeper
= 10800 × 6% = ₹ 648
Also amount of VAT received by the shopkeeper = ₹ 828
Total amount of VAT paid by shopkeeper to sale tax department = ₹ 828 – ₹ 648 = ₹ 180
Question 2.
A manufacturer of furniture sells a sofa set to a retailer for Rs. 23,000. The retailer, in turn, sells the sofa set to a customer for Rs. 29,500. Find the VAT rate as percent, if the retailer pays Rs. 520 as VAT.
Solution:
S.P. of manufacturer = Rs. 23000
or and selling price of the set to the retailer
= Rs. 29500
or cost price of the set to the customer = Rs. 29500
VAT paid by the retailer = Rs. 520
VAT paid by the manufacture = Rs. (29500 – 23000) = Rs. 6500
∴ Rate of VAT

Question 3.
Mr Kumar has recurring deposit account in a bank for 4 years at 10% p.a. rate of interest. If he gets ₹ 21,560 as interest at the time of maturity, find :
(i) the monthly instalment paid by Mr Kumar.
(ii) the amount of maturity of this recurring deposit account.
Solution:
Interest received on recurring deposit = ₹ 21560
Rate of interest (r) = 10% p.a.
Period (n) = 4 years or 48 months
(i) Let monthly instalment (P) = ₹ x

∴ Monthly instalment = ₹ 2200
(ii) Amount of maturity = P × n + Interest
= ₹ 2200 × 48 + 21560
= ₹ 105600 + 21560
= ₹ 127160
Question 4.
The maturity value of a cumulative deposit account is Rs. 1,20,400. If each monthly instalment for this account is Rs. 1,600 and the rate of interest is 10% per year, find the time for which the account was held.
Solution:
Maturity value of a cumulative deposit = Rs. 1,20,400
Deposit per month = Rs. 1600
Rate if interest (r) = 10 %
Let period = n months
∴ Principal for 1 month

20n2 + 20n = 3 (120400 – 1600n).
⇒ 20n2 + 20n = 361200 – 4800n
⇒ 20n2 + 20n + 4800n – 361200 = 0
⇒ 20n2 + 4820n – 561200 = 0
n2 + 241 n – 18060 = 0 (Dividing by 20)
⇒ n2 + 301 n — 60n – 18060 = 0
⇒ n (n + 301) – 60 (n + 301) = 0
⇒ (n + 301) (n – 60) = 0
Either n + 301 = 0, then n = -301 which is not possible or n – 60 = 0 then n = 60
∴ Period = 60 months or 5 years
Question 5.
Rajat invested Rs. 24,000 in 7% hundred rupee shares at 20% discount After one year, he sold these shares at ₹ 75 each and invested the proceeds in 18% twenty five rupee shares at 64% premium. Find :
(i) his gain or loss after one year.
(ii) his annual income from the second investment.
(iii) the percentage of increase in return on his original investment.
Solution:
In first case,
Investment = ₹ 24000,
He invested in 7% hundred rupees shares at 20% discount
∴ Market value = 100 – 20 = ₹ 80
∴ Number of shares purchased = \(\frac{24000 \times 1}{80}\)
= 300
and amount of dividend = \(\frac{24000 \times 7}{80}\)
= ₹ 2100
In second case, by selling 300 shares at the rate of ₹ 75
= 300 × ₹ 75 = ₹ 22500
Total investment = 22500 + 2100 = ₹ 24600
By investing ₹ 24600 in 18% share at 64% per annum
= \(\frac{24600 \times 18}{164}\) = ₹ 2700
(i) ∴ Gain = ₹ 2700 – ₹ 2100 = ₹ 600
(ii) Income from second investment = ₹ 2700
(iii) Percentage of increase = \(\frac{600 \times 100}{24000}=\frac{5}{2} \%\)
= 2.5%
Question 6.
A man sold some? 20 shares, paying 8% dividend at 10% discount and invested the proceeds in ? 10 shares paying 12% dividend, at 50% premium. If the change in his annual income is ₹ 600, find the number of shares sold by the man.
Solution:
Change in income = ₹ 600
Let number of shares = x
In first case,
Face value = ₹ 20
Market value at 10% discount
= \(20 \times \frac{90}{100}\) = ₹ 18
Rate of dividend = 8%
.’. Total dividend = x × \(\frac{8 \times 20}{100}\)
= ₹ \(\frac{8}{5} x\)
In second case,
Investment = x × ₹ 18 = ₹ 18x
Face value = ₹ 10
M. value = ₹ 50% premium

∴ Number of shares = 3750
Question 7.
Find the values of x, which satisfy the inequation:
\(-2 \leq \frac{1}{2}-\frac{2}{3} x \leq 1 \frac{5}{6}, x \in \mathrm{W}\)
Graph the solution on the number line.
Solution:
Here in \(-2 \leq \frac{1}{2}-\frac{2}{3} x \leq 1 \frac{5}{6}\)
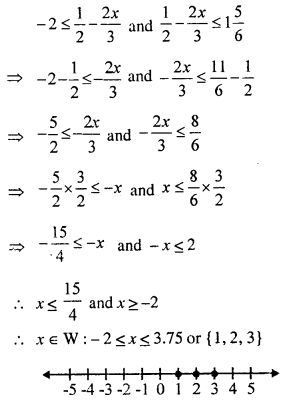
Question 8.
Solve (using formula) the equation
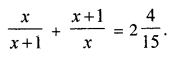
Solution:
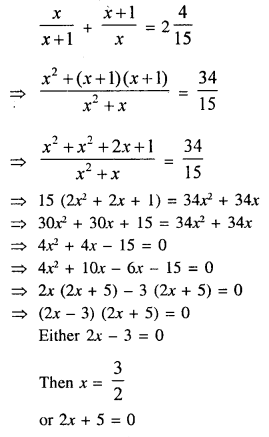
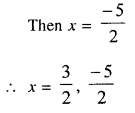
Question 9.
By selling an article for ₹ 24, a man gains as much percent as its cost price. Find the cost price of the article.
Solution:
Let CP = ₹ x
∴ Gain = x%
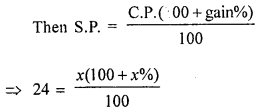
⇒ 100x + x2 = 2400
⇒ x2 + 100x – 2400 = 0
⇒ x2 + 120x – 20 – 2400 = 0
⇒ x(x + 120) – 20(x + 120) = 0
⇒ (x – 20) (x + 120) = 0
Either x – 20 = 0, then x = 20 or x + 120 = 0, then x ≠ -120
∵ C.P. cannot be negative
∴ Cost price = ₹ 20
Question 10.
B takes 16 days less than A to do a certain piece of work. If both woring together can complete the work in 15 days. In how many days will B alone complete the work?
Solution:
Let A can do a piece of work in = x days
∴ B will do the same work in = (x – 16) days But Both A and B can do the work in = 15 days.
Now A’s 1 day’s work = \(\frac{1}{x}\)
B’s 1 day’s work = \(\frac{1}{x-16}\)
Both will do the work in one day =\(\frac{1}{5}\)
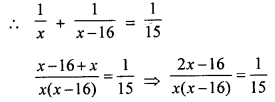
⇒ x(x – 16) = 15(2x – 16)
⇒ x2 – 16x = 30x – 240
⇒ x2 – 16x – 30x + 240 = 0
⇒ x2 – 46x + 240 = 0
⇒ x2 – 6x – 40 + 240 = 0
⇒ x (x – 6) – 40 (x – 6) = 0
⇒ (x – 6) (x – 40) = 0
Either x – 6 = 0, then x = 6 which is not possible
or x – 40 = 0, then x = 40 B will do the whole work in = 40 – 16 = 24 days
Question 11.
Divide ₹ 1,870 into three parts in such a way that half of the first part, one-third of the second part and one-sixth of the third part are all equal.
Solution:
Total amount = ₹ 1870
Let in each case, the result is x
Then \(\frac{1}{2}\) of first share = \(\frac{1}{3}\) of second share = \(\frac{1}{6}\) of third share = x.
∴ First share = 2x
Second share = 3x
and third share = 6x
∴ 2x + 3x + 6x = 1870
⇒ 11x = 1870
⇒ \(x=\frac{1870}{11}=170\)
∴ First share = 2x = 2 × 170 = ₹ 340
Second share = 3x = 3 × 170 = ₹ 510
Third share = 6x = 6 × 170 = ₹ 1020
Question 12.
If a + c = bm and \(\frac{1}{b}+\frac{1}{d}=\frac{m}{c}\), prove that a b c and d are in proportion
Solution:
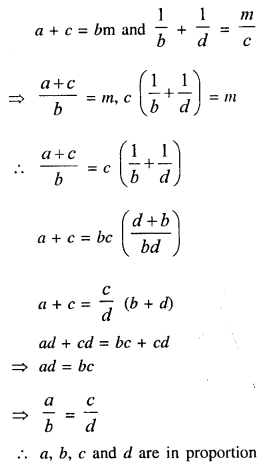
Question 13.
If \(\frac{4 x+3 y}{4 x-3 y}=\frac{7}{4}\), use properties to find the value of \(\frac{2 x^{2}-11 y^{2}}{2 x^{2}+11 y^{2}}\).
Solution:
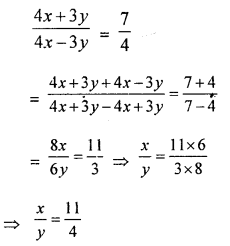
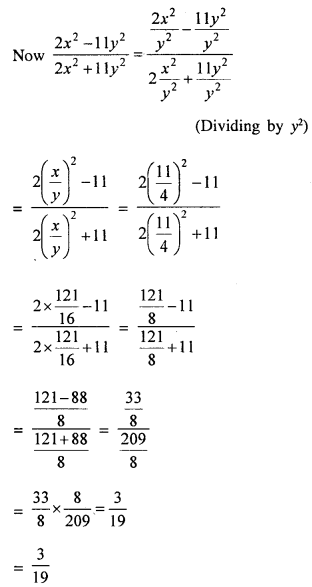
Question 14.
Use the properties of proportionality to solve
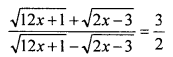
Solution:

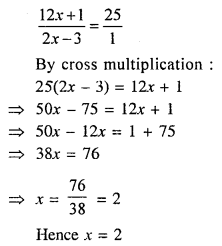
Question 15.
What number should be added to 2x3 – 3x2 – 8x + 3 so that the resulting polynomial leaves the remainder 10 when divided by 2x + 1 ?
Solution:
Let p{n) = 2x3 – 3x2 – 8x + 3
and 2x + 1 = 0, then 2x = – 1
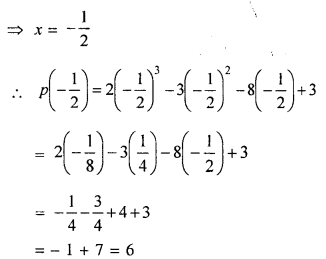
But remainder is given = 10
∴ 10 – 6 = 4 is to be added
Hence 4 is to be added
Question 16.
If \(A=\left[\begin{array}{ll}{1} & {-1} \\ {z} & {-1}\end{array}\right], B=\left[\begin{array}{cc}{x} & {1} \\ {4} & {-1}\end{array}\right]\) = A2 + B2 = (A2 + B2) find the value of x. State, whether A2 – B22and (A + B)2 are always equal or not.
Solution:
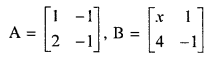
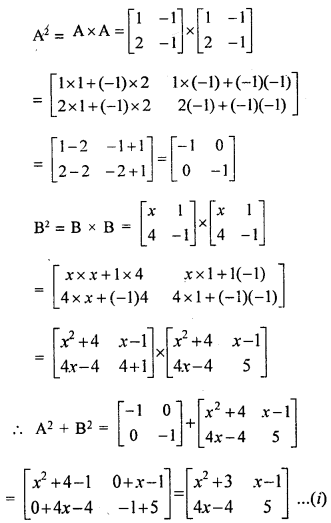
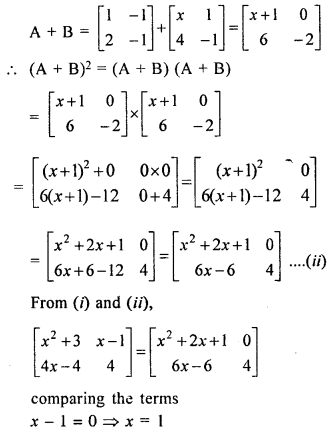
Hence x = 1
Question 17.
Find the 10th term of the sequence 10, 8, 6, …..
Solution:
Sequence is 10, 8, 6, ……
Here inA.P.
a= 10 and d= 8 – 10 = -2
∴ T10 = a + (n – 1)d = 10 + (10 – 1) × (-2)
= 10 + 9 × (-2) = 10 -18 = -8
Question 18.
If the 5th and 11th terms of an A.P. are 16 and 34 respectively. Find the A.P., …..
Solution:
In an A.P.
5th term = 16
11th term=34
Let a be the first term and d be the common difference, then
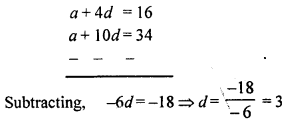
a + 4 × 3 = 16 ⇒ a + 12 = 16
a = 16 – 12 = 4
∴ A.P. is 4, 7, 10, 13, 16,
Question 19.
If pth term of an A.P. is q and its qth term is p. Show that its rth term is (p + q – r).
Solution:
pth term = q
qth term = p
Show that (p + q – r) is rth term
Let a be the first term and d be the common difference
∴ pth term = a + (p – 1)d=q
qth term = a + (q – 1 )d=p
Subtracting,
(p – 1 – q + 1 )d = q – p
(p – q)d = q – p
\(d=\frac{-(p-q)}{p-q}=-1\)
∴ a + (p – 1)(-1) = q
a + (-p) + 1 = q ⇒ a = p + q – 1
Now Tr = rth term
a + (r – 1)d
= (p + q – 1) + (r – 1)(-1)
= p + q – 1 – r + 1
= p + q – r
Question 20.
If nth term of an A.P. is (2 n -1). Find its 7th term.
Solution:
nth term of an A.P. = 2n – 1
∴ 7th term = 2n – 1
= 2 × 7 – 1 = 14 – 1 = 13
Question 21.
If the sum of first n terms of an A.P. is 3n2 + 2n, find its rth term.
Solution:
Sum of first n terms = 3n2 + 2n
∴ 1st term(a) = 3(1)2 + 2(1) = 3 + 2 = 5
2nd term = S2 – S1 = 3(2)2 + 2 × 2 – 5
= 12 + 4 – 5
= 16 – 5 = 11
∴ d = T2 -T1 = 11 – 5 = 6
∴ Tr or rth term = a + (r – 1 )d
= 5 + (r – 1) x 6
= 5 + 6r – 6 = 6r – 1
Question 22.
For an A.P., the sum of its terms is 60, common difference is 2 and last term is 18. Find the number of terms in the A.P.
Solution:
Let number of terms in the A.P. = n
Then Sn = 60, d = 2, l = 18
l = a + (n – 1 )d
18 = a + (n – 1) × 2 = a + 2n – 2
a + 2n = 18 + 2 = 20 ⇒ a = 20 – 2n …(i)
\(\frac{n}{2}\)[2a + (n – 1)d] = 60
⇒ \(\frac{n}{2}\)[a + a + (n – 1)d] = 60
⇒ \(\frac{n}{2}\)[a + 18] = 60
⇒ n(a+18) = 120
n(20 – 2n + 18)= 120 ⇒ n(38 – 2n) = 120
38n -2n2 – 120 = 0
-2n2 + 38n – 120 = 0
n2 – 19n + 60 = 0
⇒ n2 = 4n – 15n + 60 = 0
⇒ n(n – 4) – 15(n – 4) = 0
⇒ (n – 4) (n – 15) = 0
Either n – 4 = 0 then n = 4 or n – 15 = 0, then n= 15
∴ n = 4 or 15
Question 23.
Find the geometric progression whose 5th term is 48 and 8th term is 384.
Solution:
In G.P.
T5 = 48, T8 = 384
Let a be the first term and r be the common ratio
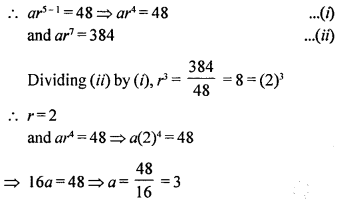
∴ GP. will be 3, 6, 12, 24,
Question 24.
Sum of how many terms of the G.P. \(\frac{2}{9}-\frac{1}{3}+\frac{1}{2}\) – …….. is \(\frac{55}{72}\) ?
Solution:
G.P. is \(\frac{2}{9}-\frac{1}{3}+\frac{1}{2}\)
Sum = \(\frac{55}{72}\)
Let a be the first term and r be the common difference.

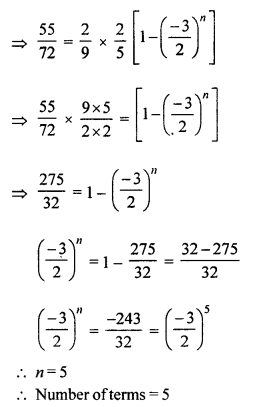
Question 25.
Find the sum of n terms of the sequence: 5 + 55 + 555 + ………
Solution:
5 + 55 + 555 + …… n term
5[1 + 11 + 111 + ………n terms]

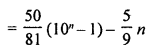
Question 26.
What point on x-axis is equidistant from the points (6, 7) and (4, -3) ?
Solution:
∵ The point is on x-axis
∴ its y = 0
Let the point be (x, 0)
Then distance between (x, 0) and (6, 7) is equal to the distance between (x, 0) and (4, -3)
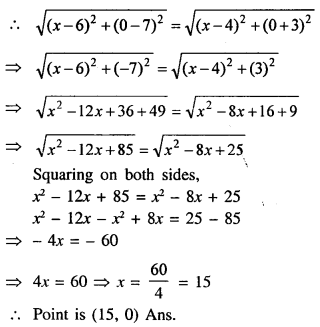
Question 27.
Calculate the ratio in which the line segment A(6, 5) and B(4, -3) is dividend by the line y = 2.
Solution:
∵ The line y = 2 is parallel to x-axis
Let the point P be (x, 2) which divided The line segment joining the points A(6, 5), B(4, -3)
Let the ratio be m1 : m2
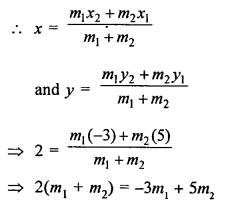
⇒ 2m1 + 2m2 = -3m1 + 5m2
⇒ 2m1 + 3m1 = 5m2 – 2m2
⇒ 5m1 = 3m2
\(\frac{m_{1}}{m_{2}}=\frac{3}{5}\)
∴ Ratio is 3 : 5
Question 28.
Find the equations of the diagonals of a rectangle whose sides are x + 1 = 0, x – 4 = 0, y + 1 = 0 and y – 2 = 0.
Solution:
∵ Lines x + 1 = 0 and y – 4 = 0 are parallel to y-axis and lines y + 1 = 0 and y – 2 = 0 are parallel to x-axis which form a rectangle ABCD.
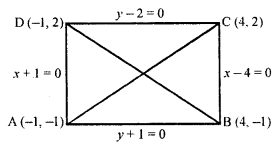
∴ Co-ordinates of A will be (-1, -1), of B will be (4, -1) of C will be (4, 2) and of D will be (-1, 2)
∵ AC and BD are the diagonals of the given rectangle ABCD.
∴ Equation of AC
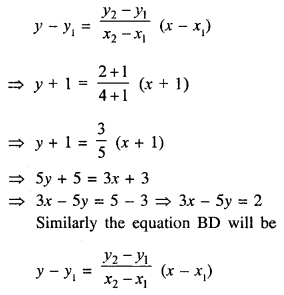
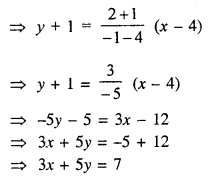
Hence equations of diagonals are 3x – 5y – 2 and 3x + 5y = 1
Question 29.
The line 4x + 5y + 20 = 0 meets x-axis at point A and y-axis at point B. Find :
(i) The co-ordinate of points A and B
(ii) The co-ordinates of point P in AB such that AB : BP = 5 : 3.
(iii) The equation of the line through P and perpendiculars to AB.
Solution:
(i) The equation of given line is
4x + 5y + 20 = 0
∵ If meets x-axis at A
∴ its y = 0
Then 4x + 5 × 0 + 20 = 0
⇒ 4x + 20 = 0
⇒ 4x = -20
⇒ \(x=\frac{-20}{4}=-5\)
∴ Co-ordinates of A will be (-5, 0)
∵ It meets y-axis at B.
∴ its x = 0
Then 4 × 0 + 5y + 20 = 0
⇒ 5y + 20 = 0 ⇒ 5y = -20
⇒ \(y=\frac{-20}{5}=-4\)
∴ Co-ordinates of B will be (0, -4)
(ii) Let point P(x, y) divides the line AB in such way that AB : BP = 5 : 3
AB = AP + PB
⇒ 5 = AP + 3
⇒ AP = 5 – 3 = 2
∴ AP : PB = 2 : 3
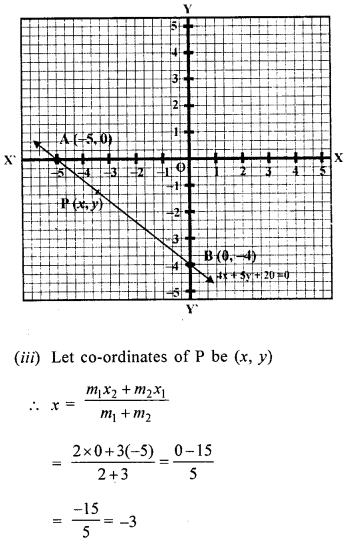

Question 30.
In the given figure, DE || BC and AE : EC = 5:4, find :
(i) DE : BC
(ii) DO : DC
(iii) are of ∆DOE : area of ∆DCE

Solution:

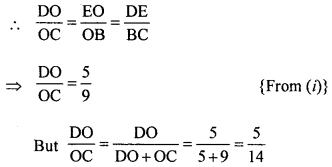
∴ DO : DC = 5 : 14
(iii) ∵ ∆DOE and ∆DCE are on the same line and their vertex is common.
∴ area of (∆ DOE): area of (∆ DCE) = DO : DC
= 5 : 14 {Proved in (ii)}
Question 31.
If chords AB and CD of a circle intersect each other at a point inside the circle, prove that PA × PB = PC × PD.
Solution:
Given : Two chords AB and CD of a circle such that they intersect each other at a point P lying inside the circle
To prove : PA × PB = PC × PD
Construction : AC and BD are joined at P
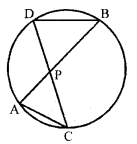
Proof : In the above figure, P lies inside the circle
In ∆s PCA and ∆s PBD, we have
∠ PCA = ∠ PBD [Angles in the same segment]
∠ APC = ∠ BPD [Vertically opposite angles]
∴ ∆PCA ~ ∆PBD [AA similarity]
Hence, \(\frac{P A}{P D}=\frac{P C}{P B}\) or PA × PB = PC × PD
Hence proved.
Question 32.
P and Q are centres of circles of radii 9 cm and 2 cm respectively. PQ = 17 cm. R is the centre of a circle of radius x cm which touches the above circles externally. Given that ∠PRQ = 90°, write an equation in x and solve it.
Solution:
P and Q are the centres of radii 9 cm and 2 cm respectively where PQ = 12 cm. R is the centre of another circle which touches the other circles such that ∠PRQ = 90°
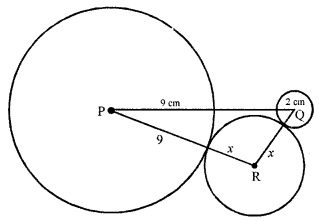
Now in right ∆ PQR,
PQ2 = PR2 + QR2
⇒ (17)2 = (9 + x)2 + (2 + x)2 (Pythagoras theorem)
⇒ 289 = 81 + 18x + x2 + 4 + 4x + x2
⇒ 2x2 + 22x + 85 – 289 = 0
⇒ 2x2 + 22x – 204 = 0
(i) ∴ x2 + 11x – 102 = 0 (Dividing by 2)
⇒ x2 – 6x + 17x – 102 = 0
⇒ x(x – 6) + 17 (x – 6) = 0
⇒ (x – 6) (x + 17) = 0
Either x – 6 = 0 then x = 6 or x + 17 = 0 then x = -17 But it is not possible.
(ii) ∴ x = 6
Question 33.
Use ruler and a pair of compasses only in this question :
(i) Draw circle on AB = 6.4 cm as diameter.
(ii) Construct another circle of radius 2.5 cm to touch the circle in (i) above and the diameter AB produced.
Solution:
Steps of construction :
(i) Draw a line segment AB = 6.4 cm.
(ii) Bisect AB at D.
(iii) With centre D and diameter AB, draw a circle
(iv) Draw a line LM parallel to AB at a distance of 2.5 cm.
(v) With centre D and radius 3.2 + 2.5 = 5.7 cm, draw an arc intersecting the line LM at 0.
(v) With centre 0 and radius 2.5 cm, draw a circle which touches the given circle at E and AB produced at C.
This is the required circle.

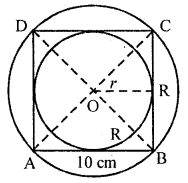
P.Q. The side of a square is 10 cm. Find the . area of the circumscribed and inscribed circles.
Solution:
Side of the square (a) = 10 cm
∴ Radius of the inscribed circle (r) = \(\frac{1}{2}\) a = \(\frac{10}{2}\) = 5cm

Question 34.
The internal and external diameters of a hollow hemispherical vessel are 14 cm and 21 cm respectively. The cost of silver plating of 1 cm2 of its surface is ₹ 32. Find the total cost of silver plating the vessel all over.
Solution:
In a hollow hemispherical vessel,
The external diameter = 21 cm
and internal diameter = 14 cm
∴ Outer radius (R) = \(\frac{21}{2}\) cm
and Inner radius = \(\frac{14}{2}\) = 7 cm
Total surface area of the bowl
= 2πR2 + 2πr2 + (πR2 – πr2.)
= 2πR2 + 2πr2 + πR2 – πr22
= 3πR2 + πr2
Question 35.
Prove that:
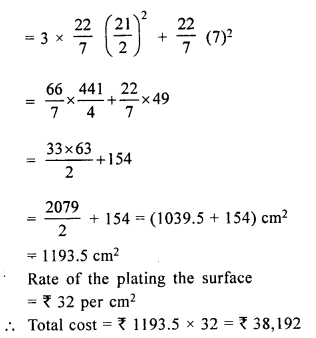
Solution:




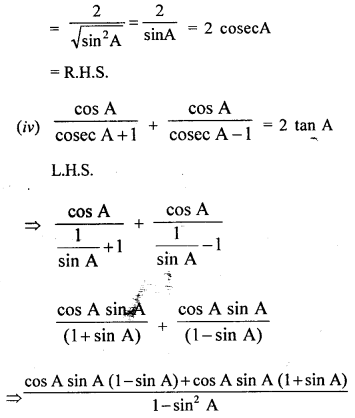

Question 36.
Solve for x, 0° ≤ x ≤ 90°
(i) 4 cos2 2x – 3 = 0
(ii) 2 sin2 x – sin x = 0
Solution:
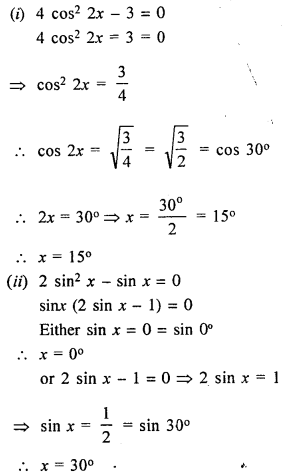
Question 37.
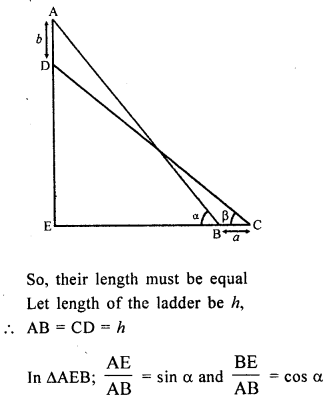
A ladder rests against a wall at an angle a to the horizontal. Its foot is pulled away from the wall through a distance a, so that it slides is distance b down the wall making an angle β with the horizontal. Show that :
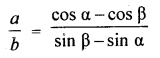
Solution:
In the figure AB and CD represent the same ladder:

Question 38.
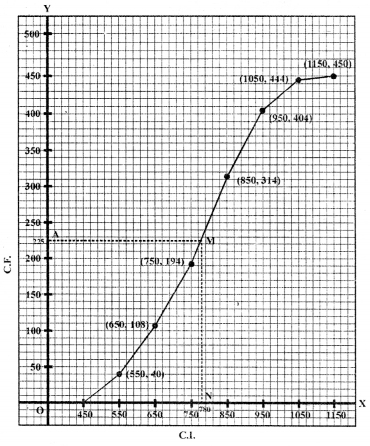
For the following frequency distirubtion, draw an ogive and then use it to estimate median.
| C.I. | 450-550 | 550-650 | 650-750 | 750-850 | 850-950 | 950-1050 | 1050-1150 |
| f | 40 | 68 | 86 | 120 | 90 | 40 | 6 |
For the same distribution, as given above, draw a histogram and then use it to estimate the mode.
Solution:
| C.I. | f | Cf |
| 450-550 | 40 | 40 |
| 550-650 | 68 | 108 |
| 650-750 | 86 | 194 |
| 750-850 | 120 | 314 |
| 850-950 | 90 | 404 |
| 950-1050 | 40 | 444 |
| 1050-1150 | 6 | 450 |
Taking C.l. on x-axis and C.I. on y-axis.
Plot the points (550, 40), (650, 108) (750, 194), (850, 314), (950, 404), (1050, 444) and (1150, 450) on the graph and join them with free hand to obtain an ogive which is shown.
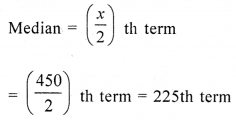
on y-axis, mark A = 225 and from A, draw a line parallel to x-axis meeting it at M. From M, draw a perpendicular on x-axis meeting it at N.
∴ M is the median which is 780 approximately Hence median = 780
Histogram :
(i) Take C.I. along x-axis and/along y-axis. Draw the histogram as shown in the figure.
(ii) In side the highest rectangle which represented the maximum frequency Join AC and BD from upper corners C and D of the adjacent rectangle which intersect each other at P.

From P, draw a perpendicular PM on x-axis M is the required mode which is 803 (approx)
Hence mode = 803
Question 39.
(i) Find the probability of drawing an ace or a jack from a pack of 52 cards.
(ii) A bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball is double that of a red ball, find the number of blue balls in the bag.
Solution:
(i) Total number of ace = 4
Total number of jack = 4
Total number of cards = 52
P (Ace or.Jack) = P (Ace) T P (Jack)
\(=\frac{4}{52}+\frac{4}{52}=\frac{2}{13}\)
(ii) Let the number of blue balls be x Number of red balls = 5 Total number of balls = Number of blue balls + Number of red balls
= x + 5

Question 40.
In a single throw of two dice, what is the probability of getting
(i) a total of 9
(ii) two aces (ones)
(iii) at least one ones
(iv) doublet
(v) five on one die and six on the other
(vi) a multiple of 2 on one and a multiple of 3 on the other ?
Solution:
Two dice are thrown having 1 to 6 each on their faces
∴ Number of possible outcome = 6 × 6 = 36
(ii) A sum of them is 9 are (3, 6), (4, 5), (5, 4), (6, 3)


