Plus Two Maths Notes Chapter 5 Continuity and Differentiability is part of Plus Two Maths Notes. Here we have given Plus Two Maths Notes Chapter 5 Continuity and Differentiability.
| Board | SCERT, Kerala |
| Text Book | NCERT Based |
| Class | Plus Two |
| Subject | Maths Notes |
| Chapter | Chapter 5 |
| Chapter Name | Continuity and Differentiability |
| Category | Kerala Plus Two |
Kerala Plus Two Maths Notes Chapter 5 Continuity and Differentiability
Introduction
As a continuation of limits and derivatives studied in the previous years, now we are entering into a very important concept continuity and its graphical peculiarities. We also learn different methods of differentiation and introduce new class of functions such as exponential and logarithmic functions.
I. Continuity
Continuity of a function at a point
A function f(x) is said to be continuous at a point ‘a’ if the following conditions are satisfied.
- f(a) should be defined.
- Left limit should be equal to right limit, ie; \(\lim _{x \rightarrow a^{-}}\)f(x) = \(\lim _{x \rightarrow a^{+}}\) f(x)
- f(a) should be equal to the limit of the function at ‘a’. \(\lim _{x \rightarrow a^{-}}\)f(x) = \(\lim _{x \rightarrow a^{+}}\) f(x) = f(a).
Continuity of a function
A function f(x) is said to be continuousif the function is continuous at every point on its domain. Some standard continuous functions are mentioned below;
- Constant function f(x) = c, c-constant.
- Identity function f(x) = x.
- Modulus function f(x) = |x|.
- Exponential function f(x) = ex.
- Logarithmic function f(x) = log x.
- Polynomial function
f(x) = a0 + a1x + a2x2 +…….+ anxn - Rational function
f(x) = \(\frac{p(x)}{q(x)}\), P(x) & q(x) are polynomial function and q(x) ≠ 0. - Trigonometric and inverse trigonometric function.
Graphical approach:
If there is a break in the graph of a function then it is not continuous.
Algebra of Continuous functions
Suppose f and g be two real functions in their respective domains then the following are true.
1. f + g, f – g, f.g, \(\frac{f}{g}\) [g(x) ≠ 0], fog, gof are all continuous functions.
II. Differentiability
Differentiability at a point:
A function f(x) is said to be differentiable at a point ‘c’ if the following limit exists and the value of the limit is known as the first derivative of f(x) at
x = c denoted by f'(c) or \(\left(\frac{d y}{d x}\right)_{x=c}\)
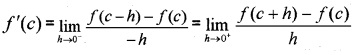
Derivative of a function:
The function defined by f'(x) = \(\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)
wherever the limit exists is defined to be the derivative of f. The derivative of f is denoted by
f ‘(x) or \(\frac{d y}{d x}\) or y’ or y1
1. Every differentiable function is continuous. But the converse need not be.true, eg; f(x) = |x|.
Some Standard Results:
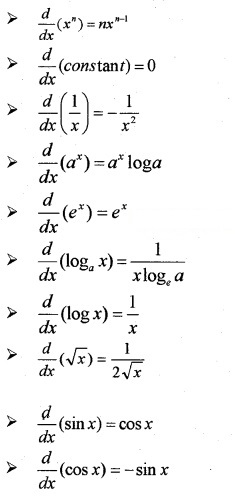

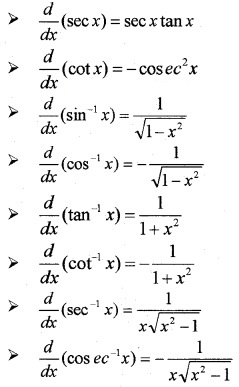
Algebra of derivatives:
Let f(x) and g(x) be two differentiable functions, then
1. \(\frac{d}{d x}\) (f(x) ± g(x)) = \(\frac{d}{d x}\)f(x) ± \(\frac{d}{d x}\) g(x).
2. Product Rule:
\(\frac{d}{d x}\)(f(x).g(x)) = \(\frac{d}{d x}\) f(x) × g(x) + f(x) × \(\frac{d}{d x}\) g(x)
3. Quotient Rule:

4. Chain Rule:
Let y be a real function which is a composite of two functions h(x) and g(x), ie; f(x) = h(g(x)) .then
\(\frac{d}{d x}\) f(x) = h'(g(x)) × g'(x).
5. Implicit Differentiation:
Here differentiate both sides of the function with respect to × and solve for \(\frac{d y}{d x}\).
6. Logarithmic Differentiation:
Function with are complicated Rational functions and of the form f(x) = u(x)v(x) is differentiated using Logarithmic Differentiation method. Here first take logarithm on both sides of the function and proceed as in implicit differentiation.
7. Parametric Differentiation:
Relation between two variable x and y which are expressed in the formx = f(t), y = g(t) is said to be parametric form with parameter t.
Here
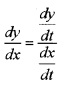
8. Second Order Derivative:
If f'(x) is differentiable we may differentiate once again with respect to x.
Then, \(\frac{d}{d x}\left(\frac{d y}{d x}\right)\) is called the Second Derivate of f with respective to x, denoted by \(\frac{d^{2} y}{d x^{2}}\) or f”(x) or y2 or y”.
III. Rolle’s theorem
Let f: [a, b] → R be a continuous function on [a, b] and differentiable on (a, b), such that f(a) = f(b) , where a and b are some real numbers. Then there exists some c ∈ (a, b) such that f'(c) = 0.
IV. Mean Value theorem
Let f: [a, b] → R be a continuous function on [a, b]and differentiable on (a, b). Then there
exists some c ∈ (a, b) such that f’(c) = \(\frac{f(b)-f(a)}{b-a}\).
We hope the Kerala Plus Two Maths Notes Chapter 5 Continuity and Differentiability help you. If you have any query regarding Kerala Plus Two Maths Notes Chapter 5 Continuity and Differentiability, drop a comment below and we will get back to you at the earliest.