Plus Two Maths Notes Chapter 13 Probability is part of Plus Two Maths Notes. Here we have given Plus Two Maths Notes Chapter 13 Probability.
| Board | SCERT, Kerala |
| Text Book | NCERT Based |
| Class | Plus Two |
| Subject | Maths Notes |
| Chapter | Chapter 13 |
| Chapter Name | Probability |
| Category | Plus Two Kerala |
Kerala Plus Two Maths Notes Chapter 13 Probability
Introduction
In this chapter we study the concept of conditional probability, multiplication rule of probability and independence of events, Baye’s theorem, Probability distribution and its mean and variance, Bernoulli Trials, Binomial Distribution, and its mean and variance.
A. Basic Concepts
I. Conditional Probability
Let A and B are two events associated with the sample space of a random experiment. The probability of occurrence of the event A that the event B has already happened is called Conditional Probability of A given B, denoted by P(A/B).
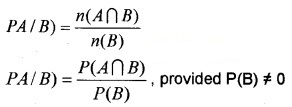
Properties:
- Let A and B be events of a sample space S of an experiment, then P(S/A) = 1, P(A/A) = 1
- If A and B are two events of a sample space S and E is an event of S such that P(E) ≠ 0, then P((A U B)/E) = P(A/E) + P(B/E) – P((A ∩ B)/E)
- P(A’/B) = 1 – P(A/B).
II. Multiplication Theorem
If A and B be two events associated with a random experiment, then
- P(A ∩ B) = P(B) × P(A/B), if P(B) ≠ 0
- P(A ∩ B) = P(A) × P(B/A), if P(A) ≠ 0
P(A ∩ B ∩ C) = P(A) × P(B / A) × P(C /(A ∩ B)).
III. Independent Events
Two events are said to be independent if the probability of occurrence of any one of the event does not affect the occurrence of the other.
- P(A/B) = P(A)
- P(A ∩ B) = P(A) × P(B)
- P(A ∩ B ∩ C) = P(A) × P(B) × P(C)
- Two events associated with a random experiment cannot be both mutually exclusive and independent.
- If P(A ∩ B) ≠ P(A) × P(B), the A and B are dependent events.
- If A and B are independent events, then
- A and \(\bar{B}\) are independent events,
- \(\bar{A}\) and \(\bar{B}\) are independent events.
IV. Theorem of total probability
Let {E1, E2,…., En}be a partition of the sample space S, and suppose that each of the events E1, E2, …., En has nonzero probability of occurrence. Let A be any event associated with S, then
P(A) = P(E1)P(A/E1) + P(E2)P(A/E2) +…….+ P(En)P(A/En)
= \(\sum_{i=1}^{n}\)P(Ei)P(A/Ei).
V. Baye’s Theorem
If E1, E2,…., En are n non-empty events which constitute a partition of sample space S, then
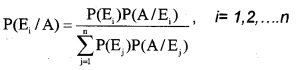
VI. Probability Distribution
The Probability Distribution of a random variable X is the system of numbers

Where the real numbers x1, x2,…….., xn are the possible values of the random variable X and p1, p2,……, Pn is the probability of the each possible values of the random variable X.
P1 + P2+…….+Pn = 1 and 0 ≤ pt ≤ 1.
- The mean of the above Probability Distribution is denoted by µ, is also called Expectation of X.
ie; Mean = µ = E(X) = \(\sum_{i=1}^{n}\)xipi - The Variance of the above Probability Distribution is denoted by σ2,
ie; Variance = σ2 = E(X2) – [E(X)]2
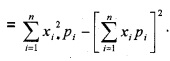
VII. Bernoulli Trial
Trials of a random experiment are called Bernoulli trial, if it satisfies the following conditions:
- There should be a finite number of trials.
- The trials should be independent.
- Each trial has exactly two outcomes: success or failure.
- The probability of success remains the same in each trial.
VIII. Binomial Distribution
Binomial Distribution, denote by B(n, p) is given (p + q)n where p represents the probability of success, q represents the probability of failure and n represents the number of trials. The probability of x success is
P(X = x) = nCxqn – xpx.
- Mean = np
- Variance = npq
- Standard Deviation = \(\sqrt{n p q}\).
We hope the Kerala Plus Two Maths Notes Chapter 13 Probability help you. If you have any query regarding Kerala Plus Two Maths Notes Chapter 13 Probability, drop a comment below and we will get back to you at the earliest.