Plus Two Maths Chapter Wise Previous Questions Chapter 1 Relations and Functions are part of Plus Two Maths Chapter Wise Previous Year Questions and Answers. Here we have given Plus Two Maths Chapter Wise Previous Chapter 1 Relations and Functions.
Kerala Plus Two Maths Chapter Wise Previous Questions Chapter 1 Relations and Functions
Plus Two Maths Relations and Functions 3 Marks Important Questions
Question 1.
Consider the set A = {1, 2, 3, 4, 5}, and B = {1, 4, 9, 16, 25} and a function ƒ : A → B defined by f(1) = 1, f(2) = 4, f(3) = 9, f(4) = 16 and f(5) = 25
(i) Show that f is one-to-one
(ii) Show that f is onto.
(iii) Does ƒ-1 exists? Explain (May – 2013)
Answer:
(i) ƒ = {(1,1), (2,4), (3,9), (4,16), (5,25)}
Every element in A is mapped to different elements in B. Therefore one-to-one.
(ii) R (ƒ) = {1, 4, 9, 16, 25} = B. Therefore onto.
(iii) Since f is one-to-one and onto function, ƒ-1 exists.
ƒ-1 = {(1,1), (4,2), (9,3), (16,4), (25,5)}
Question 2.
a) When a relation R on a set A is said to be reflexive
b) Show that ƒ : [-1, 1] → R given by \(f(x)=\frac{x}{x+2}\) is one-one (May – 2015)
Answer:
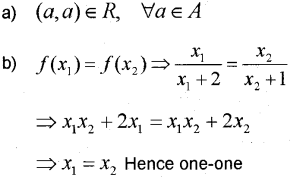
Question 3.
a) The function ƒ :N → N given by ƒ(x) = 2x
i) one-one and onto
ii) one-one and not onto
iii) not one-one and not onto
iv) onto but not one-one
b) Find goƒ(x), if ƒ(x) = 8x3 and g(x) = x1/2
c) Let * be an operation such that a*b= LCM of a and b defined on the set A = {1,2,3,4,5}. Is * a binary operation? Justify your answer. (March-2016)
Answer:
a) ii) one-one and not onto
b) Answered in previous years questions No. 2(ii) (6 Mark question)
c) LCM of 2 and 3 is 6 ∉ A, therefore not a binary operation.
Plus Two Maths Relations and Functions 4 Marks Important Questions
Question 1.
(i) ƒ : {1,2,3,4} → {5} defined by ƒ = {(1,5), (2,5), (3,5), (4,5)} Does the function is invertible?
(ii)
(iii) Let A = Nx N, N-set of natural numbers and * 1be a binary operation on A defined by (a,b) * (c,d) = (ac—bd,ud +bc). Show that* is commutative on A. (March -2011)
Answer:
(i) Inverse does not exists because fis not one-one.
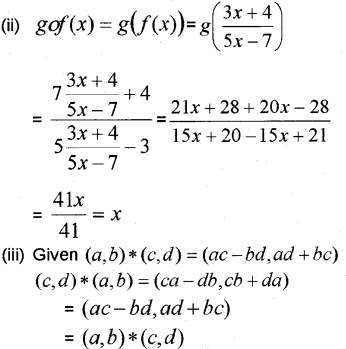
Hence cummutative.
Question 2.
Let N be the set of Natural numbers. Consider the function ƒ: N → N defined by ƒ(x) = x + l, x ∈ N
(i) Prove that f is not onto
(ii) \(If g(x)=\left\{\begin{array}{ll}x-1, & x>1 \\ 1, & x=1\end{array}\right. then find g o f\)
(iii) Check whether goƒ is an onto function. (May 2011)
Answer:
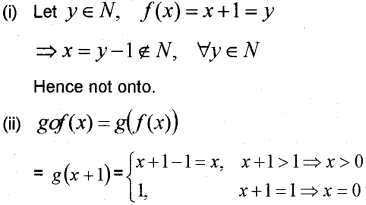
(iii) Since f is not onto goƒ is also not onto.
Question 3.
(i) Give a relation on a set A = {1,2,3,4} which is reflexive , symmetric and not transitive.
(ii) Show that ƒ : [-1,1] → R given by \(f(x)=\frac{x}{x+2}\) is one-one.
(iii) Let ‘*’ be a binary operation on Q+ defined by a*b = \(a * b=\frac{a b}{6}\) ’.Find the inverse of 9 with respect to ’ * ’. (March -2012)
Answer:
(i) Given A = {1,2,3,4}
R = {(1,1)(2,2),(3,3),(4,4),(1,2),(2,1),(1,3),(3,1)}

Question 4.
(i) *:R x R → Ris given by a * b = 3a2 – b
Find the value of 2 * 3. Is ‘*’ commutative? Justify your answer.
(ii) ƒ :R → R is defined by ƒ(x) = x2 – 3x + 2 Find ƒoƒ (x) and ƒoƒ. (May 2012)
Answer:
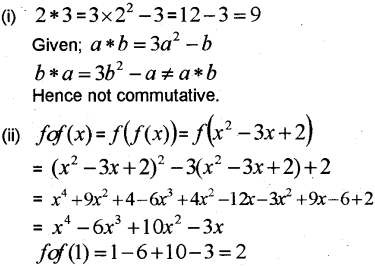
Question 5.
(i) Consider ƒ : R → R given by ƒ(x) = 5x + 2
(a) Show that f is one-one.
(b) Is f invertible? Justify your answer.
(ii) Let * be a binary operation on N defined by a * b = HCF of a and b
(a) Is * commutative?
(b) Is * associative? (March-2013)
Answer:
(i) (a) Let x1, x2, ∈ R
ƒ(x1) = ƒ(x2) ⇒ 5x1 + 2 = 5x2 + 2
⇒ 5x2 = 5x2 ⇒ x1 = x2
Therefore fis one-one.
(b) Yes.
Let y e range of ƒ
⇒ ƒ(x) = y ⇒ 5x + 2 = y
\(\Rightarrow x=\frac{y-2}{5} \in R\)
Therefore corresponding to every y ∈ R there existsa real number \(\frac{y-2}{5}\) Therefore f is onto.
Hence bijective, so invertible.
(ii) (a) Yes.
a * b = HCF (a,b) = HCF (b,a) = b * a
Hence commutative.
(b) Yes.
a * (b * c) = a* HF(b,c) = HCF(a,b,c)
(a*b) * c =HCF(a,b) * c HCF(a,b,c)
a * (b * c) = (a * b) * c
Hence associative.
Question 6.
(a) Let f: R → R be given by ƒ (x) = \(\frac{2 x+1}{3}\) find ƒoƒ and show that f is invertible.
(b) Find the identity element of the binary operation * on N defined by a * b = ab2. (May 2014)
Answer:
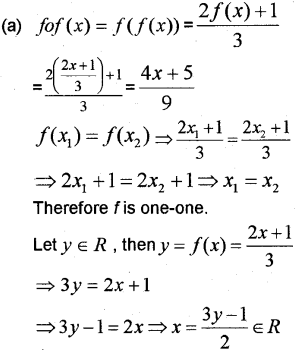
Therefore f is onto.
Hence f is bijective and invertible.
(b) let ‘e’ be the identity element, then
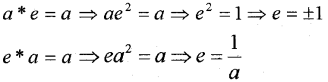
Since e is not unique, this operation has no identity element.
Question 7.
a) What is the minimum number of pairs to form a non-zero reflexive relation on a set of n elements?
b) On the set R of real numbers, S is a relation defined as S = {(x,y)/X∈R, y ∈ R, x + y = xy}. Find a ∈ R such that ‘a’ is never the first element of an ordered pair in S. Also find b ∈ R such that ‘b’ is never the second element of an ordered pair in S.
c) Consider the function \(f(x)=\frac{3 x+4}{x-2}, x \neq 2\) Find a function on a suitable domain such that goƒ(x) = x = ƒog(x). (March 2015)
Answer:
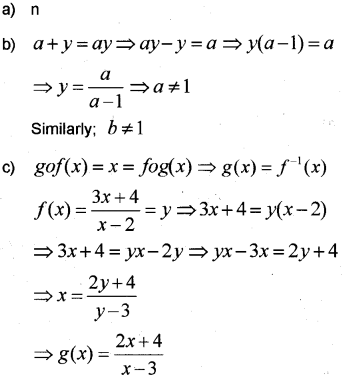
Question 8.
(i) If ƒ: R → R and g: R → R defined by ƒ(x) = x2 and g(x) = x + 1, then goƒ (x) is
(a) (x + 1)2
(b) x3 + l
(c) x2 + l
(d) x + l
(ii) Consider the function ƒ: N → N, given by ƒ(x) = x3. Show that the function ‘ƒ’ is injective but not surjective.
(iii) The given table shows an operation on A = {p,q}
| * | p | P |
| P | P | P |
| p | P | p |
(a) Is * a binary operation?
(b) * commutative? Give reason. (May 2016)
Answer:
(i) (C) x2 + 1
(ii) ƒ : N → N , given by ƒ(x) = x3
for x,y ∈ N ⇒ ƒ(x) = ƒ(y)
x3 = y3 ⇒ x = y
There fore f is injective.
Now 2 ∈ N, but there does not exists any element x in domain N such that ƒ(x) = x3 = 2 their fore f is not surjective.
(iii) (a) Yes
(b) No, because p*q = q; q*p = p
⇒ p*q ≠ q*p
Question 9.
(i) Let R be a relation defined on A{1,2,3} by R = {(13),(3,1),(2,2)} is
(a) Reflexive
(b) Symmetric
(C) Transitive
(d) Reflexive but not transitive.
(ii) Find fog and gof if ƒ(x) = |x+1| and g(x) = 2x – 1
(iii) Let * be a binary operation defined on N x N by (a,b) * (c,d.) = (a + c, b + d)
Find the identity element for * if it exists. (March – 2017)
Answer:
(i) (b) Symmetric
(ii) ƒog(x) = |g(x) + 1| = |2x – 1 + 1| = |2x|
goƒ(x) = 2 ƒ(x) – 1 = 2 |x + 1| – 1
(iii) Let e =(e1, e2) be the identity element of the operation in ? N x N then, (a,b)*(e1, e2) = (a + e1, b + e2) ≠ (a,b) Since, e1 ≠ 0, e2 ≠ 0
Therefore identity element does not existš.
Question 10.
(i) If R = {(x,y) : x, y ∈ Z, x – y ∈ Z}, then the relation R is
(a) Reflexive but not transitive
(b) Reflexive but not symmetric
(C) Symmetric but not transitive
(d) An equivalence relation.
(ii) Let * be a binary operation on the set Q of rational numbers by a*b = 2a + b. Find 2 * (3 * 4) and (2 * 3) * 4.
(iii) Let ƒ : R → R, g : R → R be two one-one funçtions. Check whether gof is one-one or not. (May- 2017)
Answer:
(i) (d) An equivalance relation.
(ii) 2* (3 * 4) = 2 * 10 = 14
(2 * 3)* 4 = 7 * 4 = 18
(iii) ƒ : R → R, g : R → R
Let x1, x2, ∈ R
goƒ(x1) = g(ƒ(x1)) = g(ƒ(x2)) = g(ƒ(x2))
⇒ x1 = x2
Plus Two Maths Relations and Functions 6 Marks Important Questions
Question 1.
(i) (a) A function ƒ : X → Y is onto if range of ƒ = ………….
(b) Let ƒ : {1, 3, 4} {3, 4, 5} and
g: {3, 4, 5} → {6, 8, 10} be functions defined by
ƒ (1) = 3, ƒ (3) = 4, ƒ (4) = 5;
g (3) = 6, g(4) = 8, g(5) = 8 ,then (goƒ) (3) = …………..
(ii) Let Q be the set of Rational numbers and ‘*’ be the binary operation on Q defined by \(a * b=\frac{a b}{4}\) for all a,b in Q
(a) What is the identity element of ‘ * ’on Q?
(b) Find the inverse element of * ’ on Q.
(c) Show that a * (b * c) = (a * b) * c, ∀a,b,c ∈ Q.
Answer:

Question 2.
(i) Let R be the relation on the set N of natural numbers given by
R = {(a,b): a – b > 2, b>3}
Choose the correct answer
(a) (4, 1) ∈ R
(b) (5, 8) ∈ R
(c) (8, 7) ∈ R
(d) (10, 6) ∈ R
(ii) If ƒ(x) = 8x3 and g(x) = x1/3, findg(ƒ(x)) and ƒ(g(x))
(iii) Let * be a binary operation on the set Q of rational numbers defined by a*b = \(\frac{a}{b}\). Check whether * is commutative and associative? (March – 2014, May – 2015, March – 2016)
Answre:
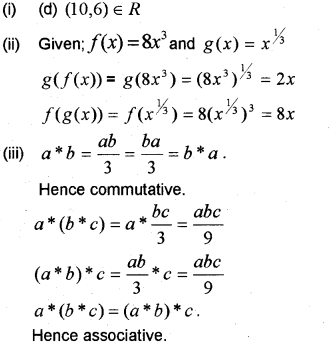
Question 3.
Let \(f(x)=\frac{x-1}{x-3}, x \neq 3\) and \(g(x)=\frac{x-3}{x-1}, x \neq 1\) be two functions defined on R.
(i) Find ƒog(x), x ≠ 0
(ii) Find ƒ-1 (x) and g-1 (x), x ≠ 1
(iii) Find (goƒ)-1 (x) (May-2010)
Answer:
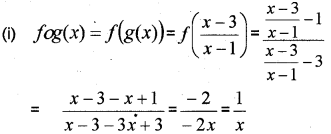
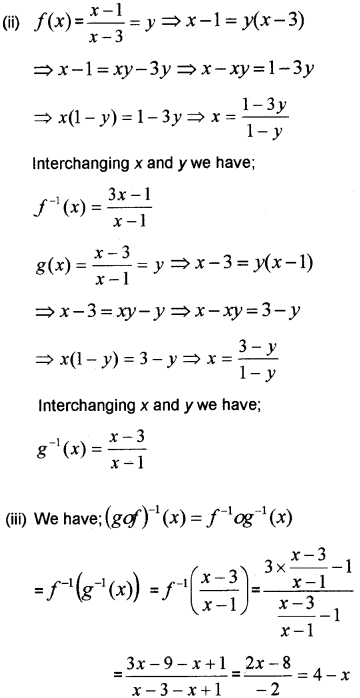
We hope the Plus Two Maths Chapter Wise Previous Questions Chapter 1 Relations and Functions help you. If you have any query regarding Kerala Plus Two Maths Chapter Wise Previous Questions Chapter 1 Relations and Functions, drop a comment below and we will get back to you at the earliest.