Plus One Physics Notes Chapter 8 Gravitation

Kerala Plus One Physics Notes Chapter 8 Gravitation

Summary
Introduction
Gravitational force is one of the fundamental forces exist in nature. All celestial bodies in the universe are moving under the influence of the gravitational force.

Kepler’S Laws
The three laws of Kepler are Known as

1. Law of orbits
2. Law of areas
3. Law of periods

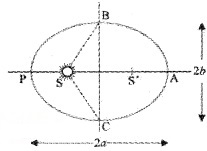
1. Law of Orbits: All planets move in elliptical orbits with the sun situated at one of the foci of the ellipse.
Ellipse:
An ellipse is a path traced out by a planet around the sun. The closest point ‘P’ is called the perihelion and Athe aphelion. The semimajor axis is half the distance AP.

Drawing an ellipse:

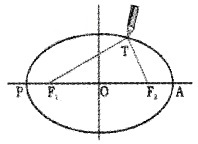
Select two points F₁ and F₂. Take a length of a string and fix its ends at F₁ and F₂ by pins. With the tip of a pencil stretch the string and then draw a closed curve. F₁ and F₂ are called the focii.

2. Law of areas: The line that joins any planet to the sun sweeps equal areas in equal intervals of time, ie. aerial velocity is constant
Proof:

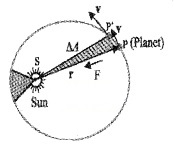
Let the sun be at the origin and let the position and momentum of the planet be denoted by \(\overrightarrow{\mathrm{r}}\) and \(\overrightarrow{\mathrm{p}}\). Let ∆\(\overrightarrow{\mathrm{A}}\) be the area swept out by the planet of mass m in time interval A t.
From the figure:

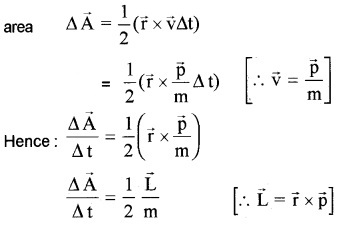
But we know angular momentum of a planet is constant because the gravitational force is central force. Hence we get \(\frac{\Delta \overline{\mathrm{A}}}{\Delta \mathrm{t}}\) = a constant.
Note:

1. Gravitational force is a central force. If direction of force on the planet is along the vector joining sun and planet, it is called central force.
2. The law of area is the consequence of conservation of angular momentum.

3. Law of periods (Kepler’s third law): The square of the time period of revolution of a planet is proportional to the cube of the semi major axis of the ellipse traced out by the planet.
T² α a³
Where ‘a’ is semi major axis.

Universal Law Of Gravitation
On the basis of Keplers laws and observations of motion of planets, Newton gave a universal law of force acting between any two particles of matter.

Statement:
Every body in the universe attracts each other with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
Explanation

Consider two masses m₁ and m₂ separated by a distance r. The force of attraction between two particles can be written as

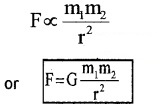
The above equation can be written in vector form as

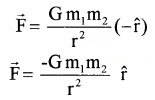
\(\hat{\mathbf{r}}\) is the unit vector from m₁ to m₂. G is a constant called the gravitational constant. In S.l. Unit G = 6.67 × 10^-11 Nm² × \(\bar{g}^{2}\).
Note:

1. The negative sign of gravitational force shows it is an attractive force.
2. \(\vec{F}_{12}=-\vec{F}_{21}\) ie; force on I^st particle due to II^nd particle = – force on II^nd particle due to I^st particle.

Deduction of Kepler’s third law:
Planet of mass m is orbiting around the sun of mass M in circular orbit of radius r, with constant angular velocity w, then.
Centripetal force = Gravitational force.

The above result holds equally good for elliptical orbit provided we replace r with a. (the semi-major axis of the ellipse)

The Gravitational Constant
The value of the gravitational constant G can be determined experimentally. This was first done by English scientist Henry Cavendish in 1798.
Cavendish experiment to determine gravitational constant:

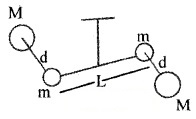
Two equal masses (m) are attached at two ends of the rod of length L. The bar is suspended from a rigid support by a fine wire. When two large lead spheres are brought close to small ones from opposite sides as shown, a deflecting torque is produced.
deflecting torque τ = F × L
= \(\frac{G M m}{d^{2}}\) × L
Where d is the distance between m and M. Due to this deflecting torque a restoring couple is produced on the wire.
For equilibrium,
Deflecting couple = Restoring couple

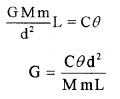
Where ‘C’ is the restoring couple per unit twist and θ is the angle of rotation. Knowing C, θ, d, M, m and L, we can calculate G. The currently accepted
value is G = 6.67 × 10^-11 Nm²/kg²

Question 1.
is it possible to shield a body from gravitational effect?
Answer:
It is not possible to shield a body from the gravitational effect because the gravitational force does not depend on the nature of the intervening medium.

Acceleration Due To Gravity Of The Earth
Acceleration due to gravity is the acceleration experienced by a body falling freely towards the earth.
Relation between acceleration due to gravity and gravitational constant:
Consider a body of mass ‘m’ at a distance ‘r’ from centre of earth. According to Newton law of
Gravitation, F = \(\frac{\mathrm{GMm}}{\mathrm{r}^{2}}\) ______(1)
Force acting on mass ‘m’
F = mg ______(2)
comparing eq(1) and eq(2)
g = \(\frac{G M}{r^{2}}\)
On the surface of earth r = R.
∴ acceleration due to gravity on the surface of earth

The value of g is 9.8 m/s². There is a slight variation for g from place to place depending on the height or depth of the place.

Question 2.
Where is the maximum value of g on the surface of earth. Why?
Answer:
It is on the poles. The distance between the pole and centre of earth is minimum at the poles. Hence
g = \(\frac{G M}{R^{2}}\) is maximum at the poles.

Question 3.
There is a popular statement regarding Convendish: “Cavendish weighed the earth”. Comment on this statement.
Answer:
Acceleration due to gravity g = \(\frac{G M}{R^{2}}\)
∴ M = \(\frac{\mathrm{gR}^{2}}{\mathrm{G}}\)
Knowing g, R, and G, we can find the mass of earth. The value of G is experimentally found out by Cavendish. This is the reason for the above statement.

Acceleration Due To Gravity Below And Above The Surface Of Earth
1. Variation of ‘g’ with altitude:
The acceleration due to gravity on the surface of earth,
g = \(\frac{G M}{R^{2}}\) _____(1)

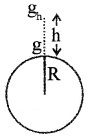
At a height h, the acceleration due to gravity can be written as,
g_h = \(\frac{\mathrm{Gm}}{(\mathrm{R}+\mathrm{h})^{2}}\) _____(2)
eq(1)/eq(2)

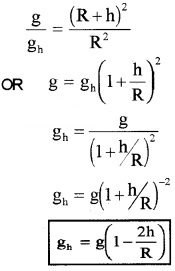
This equation shows that acceleration due to gravity decreases as height increases. The above equation is valid when h<<R.

2. Variation of g with depth:

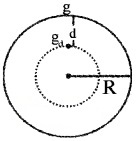
If we assume the earth as a sphere of radius R with uniform density r,
mass of earth = volume × density
M = \(\frac{4}{3}\) πR³ ρ _____(1)
We know acceleration due to gravity on the surface, GM
g = \(\frac{G M}{R^{2}}\) ______(2)
Substituting eq(1) in eq(2), we get

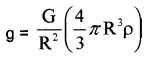
g = \(\frac{4}{3}\) πGR_ρ ______(3)
Therefore the acceleration due to gravity at a depth d is given by
g_d = \(\frac{4}{3}\) πG(R – d)ρ _______(4)
eq(4)/eq(3)

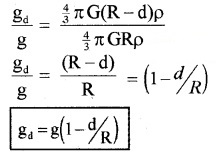
The above equatiqn shows that, when depth increases g decreases.

Gravitational Potential Energy
Gravitational potential energy:
The gravitational potential energy of a body at a point is defined as the amount of workdone in bringing the body from infinity to that point without acceleration.
Expression for gravitational P.E:

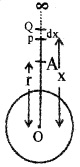
Consider the earth as a uniform sphere of radius R and mass M. Consider a point A at distance ‘r’ from the centre of earth. P is another point at a distance ‘x’ from O. Q lies at distance dx from P.

By definition, the gravitational potential energy of the body at point A, is the work done in bringing the body of mass ‘m’ from infinity to that point A. The gravitational force on the body at the point P is given by F = \(\frac{\mathrm{GMm}}{\mathrm{x}^{2}}\).
If the body is displaced from P to Q Work done,
dw = F.dx
= \(\frac{\mathrm{GMm}}{\mathrm{x}^{2}}\). Therefore, workdone in bringing the body from infinity to the point A,

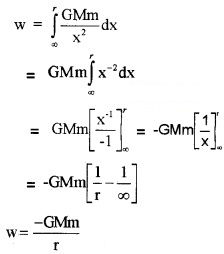
Since this workdone is stored inside the body as its gravitational potential energy, the gravitational potential energy (U) of a body of mass m at distance r from the centre of the earth is given by,

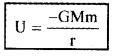
Question 4.
Gravitational potential energy at a point, U = \(\frac{-\mathrm{GMm}}{\mathrm{r}}\)

1. What is meant by negative sign in the above equation.
2. What is the value of U at r = ∞

Answer:

1. Negative sign shows that the potential energy is due to attractive gravitational force. It means, to bring a body from infinity to point P, work has been done by the gravitational field of earth, ie; by attractive force.
2. When r = ∞, the gravitational potential energy becomes zero.

Note: Maximum value of gravitational potential energy is zero.
Gravitational Potential:
The gravitational potential at a point is the amount of workdone in bringing a unit mass from infinity to that point without acceleration.
Explanation
Gravitational potential energy of mass m at a point is v = \(\frac{-\mathrm{GMm}}{\mathrm{r}}\)
If we take, m = 1 we get gravitational potential.
∴ Gravitational potential v = \(\frac{-G M}{r}\)
Note: The gravitational potential at infinity is taken to be zero.

Question 5.
What is the difference between gravitational potential energy and gravitational potential?
Answer:
Gravitational potential energy of mass m at a distance ‘r’ from centre of earth.
w = \(\frac{-\mathrm{GMm}}{\mathrm{r}}\)
But gravitational potential at a distance r from the centre of earth, w = \(\frac{-G M}{r}\)
From the equation we can understand that, gravitational potential energy depends on the mass of the body. But gravitational potential at point is independent of the mass of the body.

ESCAPE SPEED
The minimum speed with which a body is projected so that it never returns to the earth is called escape
speed or escape velocity.
Expression for escape speed:
Force on a mass m at a distance r from the centre of earth = \(\frac{\mathrm{GMm}}{\mathrm{r}^{2}}\)
Work done for giving small-displacement dr,

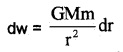
Work done in taking the body to infinity from surface of earth,

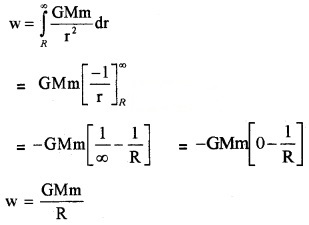
This energy is given in the form of K.E. = \(\frac{1}{2}\)mv²_e
where v_e is the escape speed

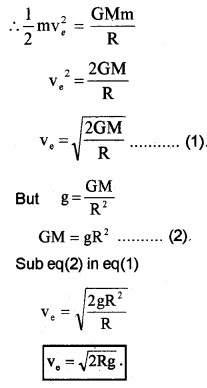
This escape velocity \(\sqrt{2 \mathrm{Rg}}\) estimated to be 11.2 km/s on the earth. But escape velocity of moon is 2.3 km/s.
Note: Escape velocity is independent of mass of the escaping body.

Question 6.
Moon has no atmosphere. Why?
Answer:
Escape velocity on moon is 2.3 km/s. The r.m.s. velocity of the gas molecules is greater than this value. Gas molecules easily escape from the surface of moon. Hence there is no atmosphere on moon.

Earth Satellites
Satellites:
The moon is the natural satellite of the earth. It goes round the earth in about 27.3 days almost in a circular. Orbit of radius 3.84 × 10⁵ km. The gravitational force of attraction between the earth and the moon supplies the necessary centripetal force to keep the moon in its circular orbit.
Artificial Satellites:
A man made satellite is called an artificial satellite.
eg: INSAT, EDUSATetc.
Orbital velocity of a satellite:
Orbital velocity of a satellite is the velocity required for a satellite to revolve round the earth in a fixed orbit.
Expression for orbital velocity:
Consider a satellite of mass m revolving with orbital velocity ‘v’ around the earth at a height ‘h’ from the surface of earth. Let M be the mass of earth and R be radius of earth.

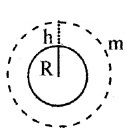
The gravitational force of attraction between earth and satellite.

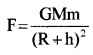
Centripetal force required for the satellite

For stable rotation,
Centripetal force = Gravitational force

The above equation shows that orbital velocity decreases as h increases.
Period of satellite:
Period of satellite is time taken by the satellite to revolve once around the planet in a fixed orbit.

Case -1
For a minimum orbit
For a satellite very close to the surface of earth, h can be neglected in comparison to R.
ie; R + h ≈ R

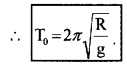
Where T₀ is called period of minimum orbit. If we substitute the value g = 9.8 m/s² and R = 6400 km,
We get

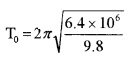
T₀ = 85 minutes.

Energy Of An Orbiting Satellite
The kinetic energy of the satellite in a circular orbit at height h from surface of earth with speed vis k.E
= \(\frac{1}{2}\) mv²

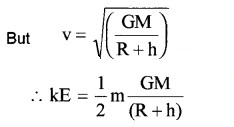
The potential energy at distance (R+h) from the centre of the earth is P.E = \(\frac{-G M m}{(R+h)}\)
∴ Total energy E = k.E. + p.E

Question 7.
What is the physical meaning of -ve energy?
Answer:
If total energy of satellite is negative, it moves in a closed path. This satellite can’t escape from earth’s gravitational field.

Question 8.
What is the condition fortotal energy to escape from earth’s gravitational field.
Answer:
If total energy of satellite is zero or positive, it can escapes to infinity.

Geostationary And Polar Satellites
A geostationary satellite is a satellite which appears to be stationary in the sky. The period of this satellite must be the same as the period of the rotation of the earth about its own axis. Its direction of rotation is from west to east.

Question 9.
Calculate the height of geostationary satellite.
Answer:
If h is the height of satellite, period

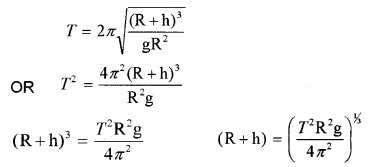
Substituting the value of
T = 24 × 60 × 60 sec., and
R= 6400 × 1000 m g = 9.8 m/s²
we get

R + h = 42648.54 km.
h = 42648.54 – R = 42648.54 – 6380
h = 36268.54 km.
Example: INSAT
Polar satellite:

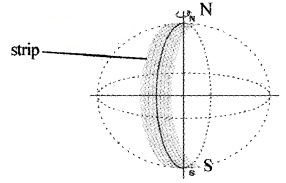
Polar satellite orbits in the north-south direction. The height of polar satellite is 500 to 800 km. Since its time period is around 100 minutes, it crosses any altitude many times a day. The camera fixed on the satellite can view small strips of the earth in one orbit.

Adjacent strips are viewed in the next orbit. So that in effect the whole earth can be viewed strip by strip during the entire day. This type of satellite is used for remote sensing, meteorology and environmental studies.

Weightlessness
A satellite can be considered to be a continuously falling body. Since a freely falling body experiences weightlessness, the satellite and object inside it feel weightlessness.

Plus One Physics Notes