Plus One Physics Notes Chapter 3 Motion in a Straight Line

Kerala Plus One Physics Notes Chapter 3 Motion in a Straight Line

Summary
Motion In A Straight Line
In this chapter, we shall learn how to describe motion. For this, we develop the concepts of velocity, acceleration and relative velocity. We also develop a set of simple equations called Kinematic equations.

• Motion: Motion is change in position of an object with time.
• Rectilinear motion: The motion along a straight line is called rectilinear motion.
• Point object: If the distance travelled by the body is very large compared with its size, the size of the body may be neglected. The body under such a condition may be taken as a point object. The point object can be represented by a point.

Example:

• The length of bus may be neglected compared with the length of the road it is running.
• The size of planet is ignored compared with the size of the orbit in which it is moving.

Position, Path Length And Displacement
1. Reference point, Frame of reference:
In order to specify position of object, we take reference point and a set of axes. Consider a rectangular coordinate system consisting of three mutually perpendicular axes, labelled x, y, and z axes. The point of intersection of these three axes is called origin (O) and serves as the reference point.

The coordinates (x, y, z) of an object describe the position of the object. To measure time, we place a clock in this coordinate system. This coordinate system along with a clock is called a frame of reference.

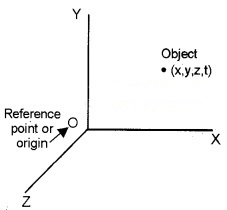
Straight-line motion in coordinate system

To describe the motion along a straight line we can choose x-axis. The position of a carat different time are given in figure 3.1. The position to the right of 0 is taken as positive and to the left of 0 as negative. The position coordinates of point P and Q are +360m +240m. The position coordinate of R is-120m.

2. Path Length (Distance):
The total length of the path travelled by an object is called path length.
Explanation:
Consider a car moving along straight line. The positions of car at different time are given in the x-axis. (See figure 3.1)
Case-1:
The car moves from 0 to P. In this case the distance moved by car is OP = +360.
Case-2:
The car moves from 0 to P and then moves back from P to Q.
In this case, the distance travelled is OP + PQ = +360 + (+120) = +480m.

3. Displacement:
The distance between initial point and final point is called displacement.
OR
The change of position of the particle in a particular direction is called displacement.
Explanation:
Consider a car moving along a straight line. The positions of car at different time is given in the x-axis.
See figure (3.1)
Let us take two cases
Case-1:
The car moves from 0 to P, in this case displacement = (360 – 0) = 360
Case-2:
The car moves from 0 to P and moves back from P to Q.
In this case,
Displacement = 240m
Let x₁ and x₂ be the positions of an object at time t₁ and t₂. Then displacement in time Dt = (t₂ – t₁) can be written as Dx = x₂ – x₁
If x₁ < x₂, Dx is positive and if x₂ < x₁, Dx is negative.
Note: The magnitude of displacement may or may not be equal to the path length traversed by an object.

4. Position Time Graph:
Motion of an object can be represented by a position-time graph.
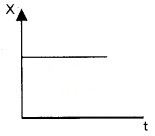
Position time graph for a stationary object:
For a stationary object, the position does not change with time. Hence the position time graph will be a straight line parallel to time axis.

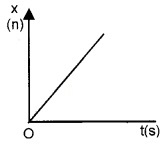
Position time graph in a uniform motion:
Uniform motion:
A body is said to be uniform motion, if it undergoes equal displacements in equal intervals of time. In uniform motion velocity is constant The figure below shows the positiontime graph of such a motion.

Question 1.
The position-time of a car is given below. Analyze the graph and explain the motion of car.

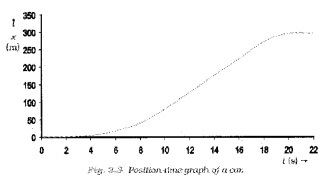
Answer:
The car starts from rest a time t=0s from the origin 0 and picks up speed till t=10s. After 10 sec, the car moves with uniform speed till t=18 sec. Then the brakes are applied and the car stops at t = 20s and x = 296m.

Question 2.
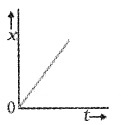
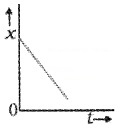
Draw the position-time for an object

1. moving with positive velocity
2. moving with negative velocity.

Answer:
1.

2.

Average Velocity And Average Speed
1. Average Velocity:
The average velocity of a particle is the ratio of the total displacement to the time interval.

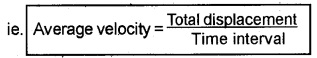
Explanation:
To explain average velocity, consider a position-time graph of a body given below.

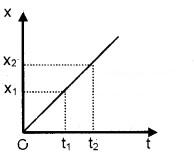
Let x₁ be the position of body at a time t₁ and x₂ be the position at t₂.
The average velocity during the time interval Dt = (t₂ – t₁)

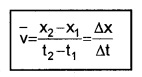
where Dx = x₂ – x₁, and Dt = t₂ – t₁,
\(\overline{\mathbf{v}}\) is the average velocity.

Question 3.
Find the slope of position-time graph given below of uniform motion and explain the result.

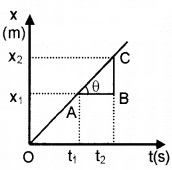
Answer:

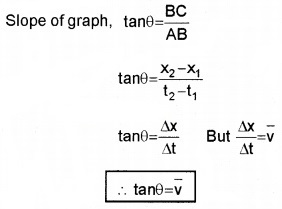
Slope of displacement time graph gives average velocity.

Question 4.
Displacement time graph of a car is given below.

1. Find the average velocity during the time interval 5 to 7 sec.
2. Find the average velocity by taking slope in the interval 5 to 7 sec.

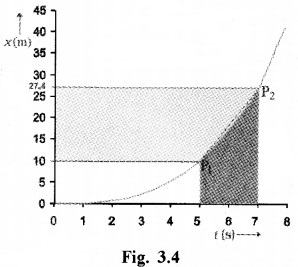
Answer:
1.

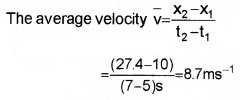
2. Slope, tan q

In this case, slope and average velocity are equal in the same interval.

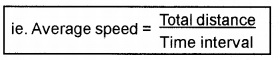
2. Average Speed:
Average speed of a particle is the ratio of the total distance to total time taken.

Question 5.
A car is moving along a straight line. Say OP in figure. It moves from 0 to P in 18s and returns from P to Q in 6s. What are the average velocity and average speed of the car in going?

1. From 0 to P? and
2. from 0 to P and back to Q. (See Figure 3.1)

Answer:
1. Average velocity

Average speed

In this case the average speed is equal to the magnitude of the average velocity.

2. In this case
Average velocity

Average speed

In this case the average speed is not equal to the magnitude of the average velocity. This happens because the motion here involves change in direction. So that the distance is greater than displacement.
Note: In general, the velocity is always less than or equal to speed.

Instantaneous Velocity And Speed
Nonuniform Motion:
A body is said to be nonuniform motion, if it undergoes unequal displacements in equal intervals of time.

OR

A body moving with varying velocity is called nonuniform motion.

1. Instantaneous Velocity:
Question 6.
Why the concept of instantaneous velocity is introduced?
Answer:
In nonuniform motion the average velocity tells us how fast the object has been moving over a given interval. But it does not tell us how it moves at different instants during that interval. For this we define instantaneous velocity. The velocity at an instant is called instantaneous velocity.
Explanation:
Position-time of a body moving along a straight line is given below.

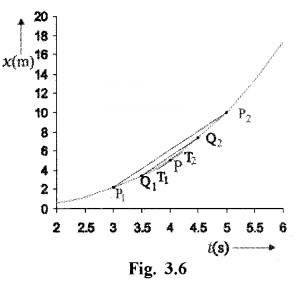
Let us find average velocity in the interval 2 sec (3s to 5s), centered at t = 4 sec. In this case, the slope of line P₁P₂ give the value of average velocity, ie. Slope of P₁P₂,

Decrease the value of Dt from 2.to 1 sec. (ie. 3.5 to 4.5 sec). Then line P₁P₂ becomes Q₁Q₂. Then the slope of gives average velocity overthe interval 3.5 sec to 4.5sec.
ie. slope of Q₁Q₂

In the limit Dt ® 0, gives the instantaneous velocity at t = 4sec and its value is nearly 3.84m/s.

Question 7.
When average velocity of a body becomes instantaneous velocity?
Answer:
In the limit, Dt goes to zero, the average velocity becomes instantaneous velocity.

But lim \(\lim _{\Delta t \rightarrow 0} \frac{\Delta x}{\Delta t}=\frac{d x}{d t}\)
\Instantaneous velocity,

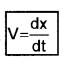
Here \(\frac{d x}{d t}\) is the differential coefficient of x with respect to time. It is the rate of change of position with respect to time at an instant.

Question 8.
The table given below gives the value of \(\frac{\Delta x}{\Delta t}\) for Dt equal to 2s, 1s, 0.55, 0.1s and 0.01s centered at t = 4 sec. (See figure given above). What conclusions can be made from this table?
Answer:
The value of average velocity \(\left(\frac{\Delta x}{\Delta t}\right)\) becomes instantaneous velocity (3.8 m/s), in the limit of Dt goes to zero, (ie Dt is infinitesimally small).

Question 9.
The position of an object moving along x-axis is given by x = a + bt² where a = 8.5m, b = 2.5 m/s² and t is measured in seconds

1. What is the velocity at t = 0s and t = 2s.
2. What is the average velocity between t = 2s and t = 4s?

Answer:
1.

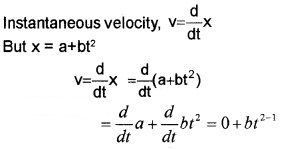
when t = 0
we get v = 2 × 2.5 × 0
v = 0
when t = 2sec
v = 2 × 2.5 × 2 v = 10m/s.

2. The average velocity

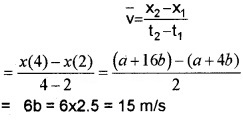
Note: If a body is moving with constant velocity, the average velocity is the same as instantaneous velocity at all instants.

2. Instantaneous Speed:
The speed at an instant is called instantaneous speed.
Note:

• The average speed over a finite interval of time is greater or equal to the magnitude of the average velocity.
• Instantaneous speed at an instant is equal to the magnitude of the instantaneous velocity at that instant.

Acceleration
1. Average Acceleration:
Average acceleration of a particle is ratio of the change in velocity to the time interval.

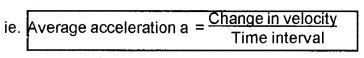
Explanation
Consider a body moving along a straight line. Let v₁ and v₂ be the instantaneous velocities at time t₁ and t₂ respectively.

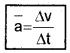
where Dv = change in velocity, Dt = Time interval

2. Instantaneous Acceleration:
Acceleration at any instant is called instantaneous acceleration.
Explanation
In the limit Dt ® 0, (Dt goes to zero) the average acceleration becomes instantaneous acceleration.
ie. Instantaneous acceleration

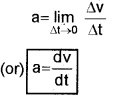
Instantaneous acceleration is the rate of change of velocity with respect to time.

3. Uniform Acceleration:
A body is said to be in uniform acceleration if velocity changes equally in equal intervals of time.

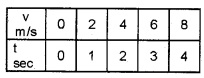
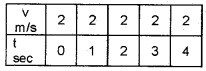
Question 10.
The velocities of two bodies A and B are given in the tables. From this table, find which body is moving with uniform acceleration. Explain.
Body A

Body B

Answer:
Body A is moving with uniform acceleration be-cause the velocity of body increases at the rate of 2 m/s².
The body B is moving with constant velocity. Hence this motion is called uniform motion.

4. Velocity-Time Graph For Uniformly Accelerated Motion:

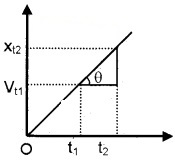
An example for velocity-time of a uniformly accelerated motion is given in the above figure.
Let v_t1 and v_t2 be the velocities at instants t₁ and t₂respectively.
The slope of graph in the interval (t₂ – t₁) can be written as,

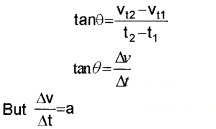
∴ tan q = acceleration
Thus the slope of the velocity-time gives the acceleration of the particle.

Question 11.
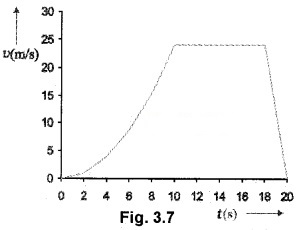
The Velocity-time of a body is given below. From this graph draw the corresponding acceleration time graph.

Answer:
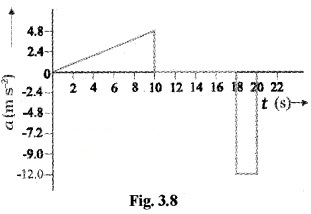
The slope of velocity-time graph increases in the interval (0 – 10) sec which means that acceleration of the body increases in this interval.

Velocity is constant in the interval (10 – 18) sec. Hence ’ the slope is zero which means that acceleration is zero in this range.

The slope in the interval (18 – 20) sec is constant and negative. Hence acceleration in this is a negative value. The acceleration – time graph for the above motion is given below.

Question 12.
The position-time graph of a car is given below.

1. Draw corresponding velocity-time graph. Explain the reason for your answer.
2. From velocity-time graph draw acceleration-time graph and identify the regions of

• positive acceleration
• Negative acceleration
• zero acceleration.

Answer:
1. In the time interval (0 – t₁) sec, the slope of x – t graph increases which means that velocity is increasing in this time interval.

In the time interval (t₁ – t₂) sec, slope is constant. Hence velocity remains constant in this time interval.

In the time interval (t₂ – t₃) sec, the slope is decreasing and finally becomes zero. Which means that velocity decreases to zero.

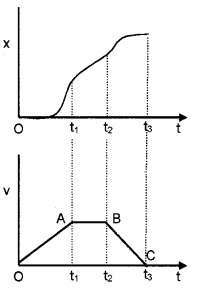
2. Slope is constant throughout the interval (0 – t₁) sec which means that acceleration constant.

In the interval (t₁ – t₂) sec, slope is zero. Which means that acceleration is zero in this region.

Slope is constant (but negative) in the interval (t₂ – t₃)sec. Hence acceleration is constant and negative in this time interval.

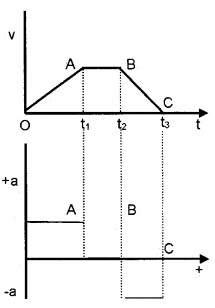
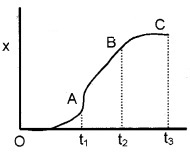
Question 13.
Find the region of

1. positive acceleration
2. zero acceleration
3. negative acceleration from the above x-t graph

Answer:

1. Region OA – Positive acceleration
2. Region AB – zero acceleration
3. Region BC – Negative acceleration

Question 14.
Match the following.

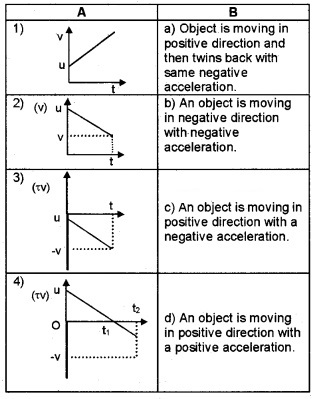
Answer:
1) – d, 2) – c, 3) – b, 4) – a.

5. Area Under Velocity-Time Graph:
Area under velocity-time graph represents the displacement over a given time interval.
Explanation
Consider a body moving with constant velocity v. Its velocity-time graph is given below.

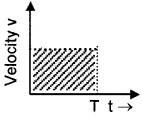
The area of the rectangle has height v and bast t. Therefore,

Note: The acceleration and velocity of a body cannot change values abruptly at an instant. Changes are always continuous.

Kinematic Equations For Uniformly Accelerated Motion
For uniformly accelerated motion, we can derive some simple equations.

1. Velocity-time relation
2. Position-time relation
3. Position-velocity relation

These equations are called kinematic equations for uniformly accelerated motion.
1. Velocity-Time Relation:

Consider a body moving along a straight line with uniform acceleration ‘a’. Let ‘u’ be initial velocity and ‘v ‘ be the final velocity at time t.
We know acceleration a = \(\frac{\text { Change in velocity }}{\text { Time interval }}\)
a = \(\frac{v-u}{t}\)
at = v – u

2. Position-Time Relation:

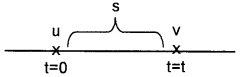
Consider a body moving along a straight line with uniform acceleration a. Let ‘u’ be initial velocity and ‘v’ be the final velocity. ‘S’ is the displacement travelled by the body during the time interval ‘t‘.
Displacement of the body during the time interval t,
S = average velocity × time
\(S=\left(\frac{v+u}{2}\right) t\) _____(1)
But v = u + at ____(2)
Substitute eq.(2) in eq.(1), we get

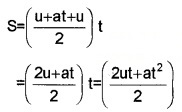
3. Position-Velocity Relation:
\(S=\left(\frac{v+u}{2}\right) t\) _____(1)
But v = u + at
\(\frac{v-u}{a}\) = t _____(2)
Substitute eq.(2) in eq.(1)

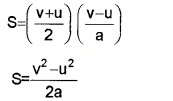
2as = v² – u²
v² – u² = 2as

Free-fall:
An object released (near the surface of earth) is accelerated towards the earth. If air resistance is neglected, the object is said to be in free fall. The acceleration due to gravity near the surface of earth is 9.8 m/s².
Note: Free-fall is a case of motion with uniform acceleration.

Question 15.
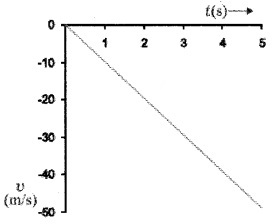
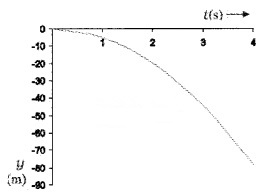
A body is allowed to fall freely. Draw the following graph.

1. Acceleration-time
2. Velocity-time
3. Position-time

Answer:
1.

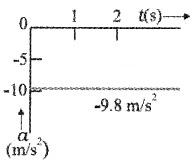
2.

3.

Stopping distance of vehicles:
When brakes are applied to a moving vehicle, the distance it travels before stopping is called stopping distance.

Question 16.
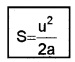
Derive an expression for stopping distance of a vehicle in terms of initial velocity (u) and retardation (a).
Answer:
Let the distance travelled by the vehicle before it stops be ‘s’.
Then we can find ‘s’ using the formula
v² = u² + 2as
0 = u² + -2as

3.7 Relative Velocity
Suppose the distance between two bodies changes with time in magnitude, or in direction or in both. Then each body is said to have a velocity relative to the other.

For example, consider two cars A and B moving in the same direction with equal velocities. To a person in A, the car B would appear to be rest.

Hence the velocity of B relative to A is zero.
ie. V_BA = 0
Similarly, the velocity of A with respect to B is zero.
or V_AB = 0
Let A be moving with a velocity V_A and B be moving with a greater velocity V_B in the same direction. Then the person in A feels that the car B is moving away from him with a velocity V_BA. The velocity of B relative to A

For an observer in B, car A is going back with a velocity. The velocity of A relative to B
V_AB = -(V_B – V_B).

Question 17.
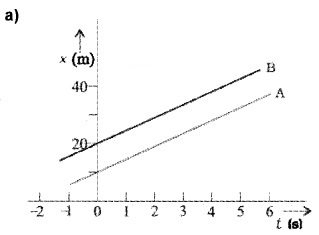
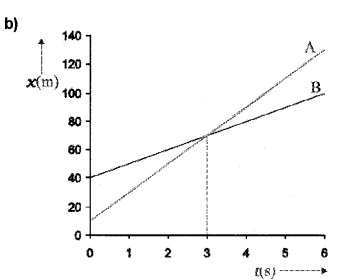
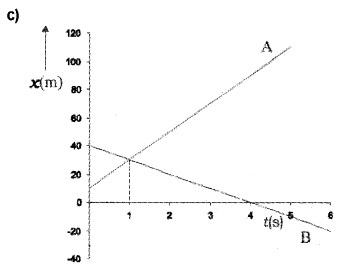
The position-time graph of two bodies A and B (at different situations) are given in the following graphs. Find the relative velocities of the following graph.

Answer:
a) The slope of Aand B are equal. Hence velocity of A and B are equal. So velocity of A with respect to B, V_AB = 0

b) The body A and B meet at t = 3sec

Velocity of A w.r. to B, V_AB = V_A – V_B
= 20-10 = 10 m/s Velocity of B w.r. to A, V_BA = V_B – V_A
= 10 – 20 = -10 m/s

c) The body A and B meet at t = 1 sec.
The velocity of body in the interval t = 1 sec,

Velocity of A w. r. to B,
V_AB = V_A – V_B
= 20 – 10 = 30 m/s
Similarly velocity of B w.r. to A,
V_BA = V_B – V_A
= 10 – +20 = -30 m/s
The magnitude of V_BA or V_AB (=30 m/s) is greater than the magnitude of velocity A or that of B.

Plus One Physics Notes