Kerala Plus One Physics Improvement Question Paper Say 2017 with Answers
| Board | SCERT |
| Class | Plus One |
| Subject | Physics |
| Category | Plus One Previous Year Question Papers |
Time: 2 Hours
Cool off time: 15 Minutes
Maximum: 60 Scores
General Instructions to candidates:
- There is a ‘cool off time’ of 15 minutes in addition to the writing time.
- Use the ‘cool off time’ to get familiar with the questions and to plan your answers.
- Read the instructions carefully.
- Read questions carefully before you answering.
- Calculations, figures, and graphs should be shown in the answer sheet itself.
- Malayalam version of the questions is also provided.
- Give equations wherever necessary.
- Electronic devices except non-programmable calculators are not allowed in the Examination Hall.
Questions 1 to 5 has 1 score each. Answer any four. (4 × 1 = 4)
Question 1.
Name the weakest force among the fundamental forces.
Answer:
Weak nuclear force
Question 2.
The work done during an isochoric process is …………
Answer:
Zero
Question 3.
Highway police detect over speeding vehicles by using ………….
Answer:
a) Magnus effect
b) Pascal’s law
c) Doppler effect
d) Bernoulli’s theorem
Answer:
c) Doppler effect
Question 4.
Two forces 3N and 4N are acting perpendicular to each other. The magnitude of the resultant force is
a) 7N
b) 1N
c) \(\sqrt{49}\)N
d) 5N
Answer:
d) A = 4, B = 4, θ = 90°
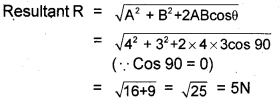
Question 5.
Say true/false: “Trade winds are produced due to conduction.”
Answer:
False
Questions 6 to 11 has 2 scores each. Answer any five. (5 × 2 = 10)
Question 6.
The displacement (S) of a body in a time ‘t’ is given by S = at2 + bt. Find the dimensions of a and b.
Answer:
6. S = at2 + bt
S = at2, L = a × T2, a = \(\frac{L}{T^{2}}\) = LT-2
S = bt, L = b × T, b = \(\frac{L}{T}\) = LT-1
Question 7.
Give the magnitude and direction of the net force on a stone of mass 0.1 kg
a) Just after it is dropped from the window of a train accelerating 1 ms-2.
b) Lying on the floor of a train which is accelerating with 1 ms-2, the stone being at rest relative to the train.
Answer:
a) ω = mg
= 0.1 × 10 = 1N
b) F = mg
= 0.1 × 1 = 0.1N
Question 8.
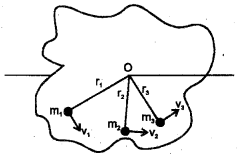
A body is rolling on a horizontal surface. Derive an equation for its kinetic energy.
Answer:
Consider a body rotating about an axis passing through some point O with uniform angular velocity ‘ω’. The body can be considered to be made up of a number of particles of masses m1, m2, m3 ………. etc at distances r1, r2, r3 …….. etc. All the particles will have same angular velocity ω. But their linear velocities will be different say v1, v2, v3, ………. etc.

Question 9.
The stress-strain graphs for two materials A and B are shown below (the graphs are drawn using the same scale) Which one is more elastic? Why?
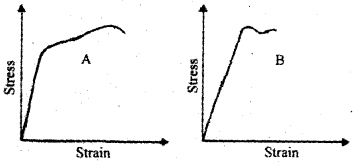
Answer:
Slope of stress strain graph give Young’s modulus. Graph A gives more slope. Flence material Ahas more Young’s modulus. Therefore Ahas more elasticity.
Question 10.
“A heavy and a light body have the same kinetic energy.” Which one has greater momentum? Why?
Answer:

Question 11.
The following figures refer to the steady flow of a non-viscous liquid. Which of the two figures is correct? Why?
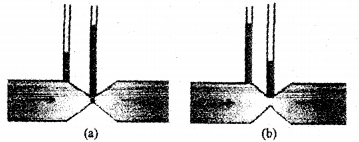
Answer:
Figure (b). When water flows through a narrow pipe, its velocity increases. Hence pressure at narrow part decreases. As a result, the height of water level decreaes at narrow part.
Questions from 12 to 17 carries three scores each. Answer any five. (5 × 3 = 15)
Question 12.
The side of a cube is measured as 3.405 cm.
a) How many significant figures are there in the measurement.
b) If the percentage error in the measurement of the side of the cube is 3%, find the percentage error in its volume.
Answer:
a) 4
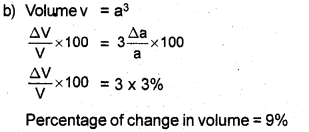
Question 13.
According to conservation of energy “energy can neither be created nor be destroyed.”
a) Prove law of conservation of mechanical energy in the case of a freely falling body.
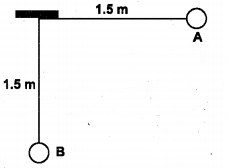
b) The bob of a pendulum of length 1.5 m is released from the position ‘A’ shown in figure. What is the speed with which the bob arrives at the lower most point B, given that 5% of its initial energy is dissipated against air resistance?
Answer:
a) Conservation of mechanical energy for a freely falling body
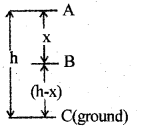
Consider a body of mass ‘m’ at a height h from the ground.
Total energy at the point A
Potential energy at A, PE = mgh
Kinetic energy KE = \(\frac{1}{2}\)mv2 = 0
(since the body at rest, v = 0).
∴ Total mechanical energy = PE + KE
= mgh + 0
= mgh
Total energy at the point B
The body travels a distance x when it reaches B.
The velocity at B, can be found using the formula.
v2 = u2 + 2as
v2 = 0 + 2gx
∴ KE at B, = \(\frac{1}{2}\)mv2
= \(\frac{1}{2}\)m2gx = mgx
PE. at B, = mg (h – x)
Total mechanical energy = PE + KE
= mg(h – x) + mgx
= mgh
Total energy at C
Velocity at C can be found using the formula
v2 = u2 + 2as
v2 = 0 + 2gh
∴ KE at C, = \(\frac{1}{2}\)mv2
= \(\frac{1}{2}\)m2gx = mgx
PE at C = 0
Total energy = PE + KE
= 0 + mgh = mgh
b) 5% energy is lost due to friction. Hence energy at bottom is

Question 14.
Acceleration due to gravity on earth changes with depth and height.
a) What is the weight of a body placed at the centre of earth? Why?
b) Find the height at which the acceleration due to gravity is \(\frac{1}{4}\)th that at the surface of earth.
Answer:
a) Zero, weight w = mg
at center g = 0, ∴w = 0
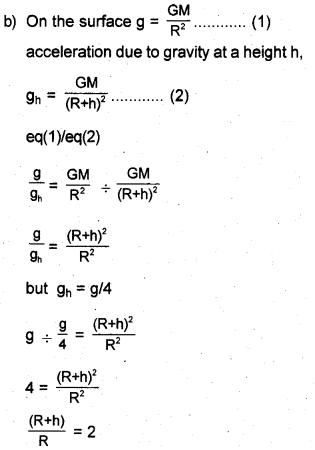
R + h = 2R
h = R
acceleration due to gravity is reduced to \(\frac{g}{4}\) at height equal to radius of earth.
Question 15.
A metal sphere of density ‘ρ’ and radius ‘a’ is falling through an infinite column of liquid of density ‘σ’ and coefficient of viscosity ‘η’.
a) Name any two forces acting on the sphere.
b) With the help of Stoke’s theorem, derive an equation for the terminal velocity of the sphere.
Answer:
a) Gravitational force and viscous force
b) If a body is moving through a fluid, its velocity is influenced by the viscosity of the medium.
Considers small sphere of radius ‘a’ falling under gravity in air: The viscocity of air opposes the motion of the sphere. This opposing force is called viscous force and can be written as.
F = 6πaηv
This is called stokes, formula.
Where η is the coefficient of viscosity of the medium and v is the velocity of the body.
Question 16.
Condition is the mode of transfer of heat in solids.
a) Write the unit of thermal conductivity
b) “Burns produced by steam is severe than that produced by boiling water” Why?
Answer:
a) JS-1m-1K-1 or Wm-1K-1
b) Steam contains more energy than boiling water.
Question 17.
A gas has ‘f’ degrees of freedom
a) Calculate its Cp, Cv and γ
b) Define mean free path.
Answer:
a) (Molar specific heat capacity)
In general a polyatomic molecule has 3 translational, 3 rotational degrees of freedom and a certain number (f) of vibrational modes.
The energy of one mole polyatomic gas,

Questions from 18 to 22 carries four scores each. Answer any four. (4 × 4 = 16)
Question 18.
A satellite moves in a circular orbit of raius ‘r’ with an orbit velocity.
a) Derive an equation for the orbit velocity of a satellite.
b) The time taken by Saturn to complete one orbit around the Sun is 29.5 times the earth year. If the distance of earth from the Sun is 1.5 × 108 km, then what will be the distance of the Saturn from the Sun?
Answer:
a) Consider a satellite of mass m revolving with orbital velocity ‘v’ around the earth at a height ‘h’ from the surface of earth. Let M be the mass of earth and R be radius of earth.
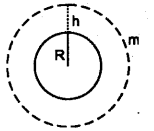
The gravitational force of attraction between earth and satellite.
F = \(\frac{\mathrm{GMm}}{(\mathrm{R}+\mathrm{h})^{2}}\)
Centripetal force required for the satellite
F = \(\frac{m v^{2}}{(R+h)}\)
For stable rotation,
Centripetal force = Gravitational force
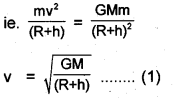
The above equation shows that orbital velocity decreases as h increases.
Period of satellite
Period of satellite is time taken by the satellite to revolve once around the planet in a fixed orbit.
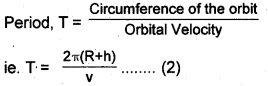

Question 19.
In simple harmonic motion, force is directly proportional to the displacement from the mean position.
a) Give an example of a harmonic oscillator.
b) Derive equations for the kinetic and potential energies of a harmonic oscillator.
c) Show graphically the variation of kinetic energy and potential energy of a harmonic oscillator.
Answer:
a) Simple pendulum
b) Expression for Kinetic energy
Let m be the mass of the particle executing SHM.
Let V be the velocity at any instant,

Expression for potential energy:
Potential energy is work required to take the particle against the restoring force.
Work done to displace the particle through a small distance dy,
dw = force × displacement
= mω2y × dy [force = mω2y ]
Therefore total workdone to take the particle from 0 to y.

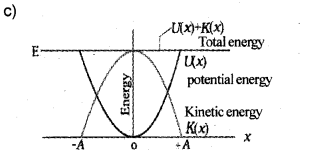
Question 20.
A stretched string can be used as a musical instrument.
a) What is the fundamental frequency of a stretched string?
b) With neat diagrams, derive equations for the second and third harmonics of a stretched string.
Answer:
a) Fundamental frequency = \(\frac{\mathrm{V}}{2 \mathrm{~L}}\)
b) The ferquency of vibrations of stretched string of length L is \(v=\frac{n V}{2 L}\), where n = 1, 2, 3, … etc.
Relation between V and L for first harmonics
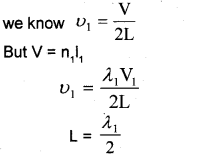
General relation can be written as L = (\(n \frac{\lambda}{2}\))
The string vibrate in a single segment as shown in figure.
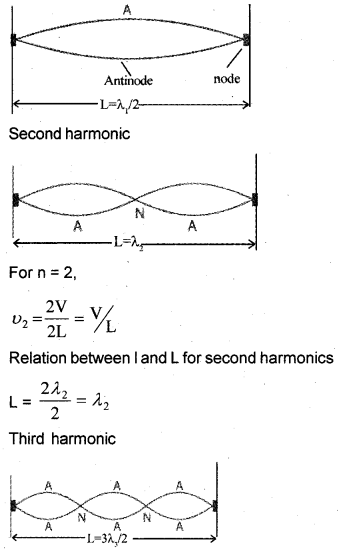
For n = 3, there is 3rd harmonic. Thus collection of all possible mode is called harmonic series and n is called harmonic number.
Question 21.
A body having an initial velocity ‘V0’ has an acceleration ‘a’.
a) Using velocity-time graph, derive an equation for displacement of the above body.
b) Draw the velocity-time graph and speed-time graph of a body thrown vertically in air.
Answer:
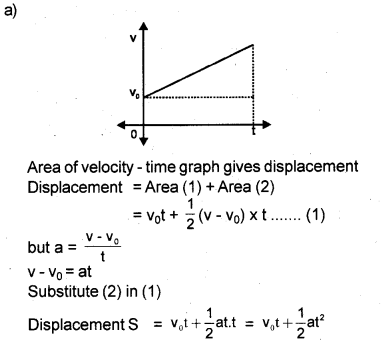
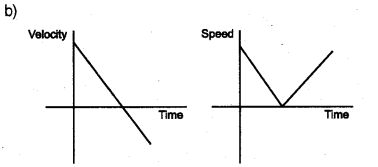
Question 22.
A javelin is thrown with an initial velocity ‘v0’ at an angle ‘θ’ with the horizontal.
a) What is the horizontal and vertical velocities c the body
i) At the point of projection
ii) At maximum height
b) Find the angle of projection at which the maximum height attained by the javelin is equal to the horizontal range.
Answer:
a) i) u cosθ and u sinθ
ii) u cosθ
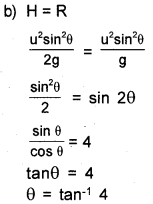
Questions 23 to 26 carries 5 scores each. Answer any 3. (3 × 5 = 15)
Question 23.
a) What is meant by ‘banking of roads’?
b) With neat diagram, derive equation for the maximum velocity of a car on a banked road.
c) What is the optimum speed of the car along the banked road?
Answer:
a) To avoid skidding the outer edge of the road slightly rises above the inner edge. This road is called banked road.
b) Motion of a car on a banked road
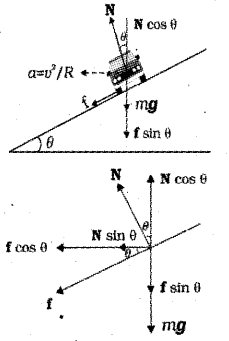
Consider a vehicle along a curved road with angle of banking θ. Then the normal reaction on the ground will be inclined at an angle θ with the vertical.
The vertical component can be divided into N Cosθ (vertical component) and N sinθ (horizontal component). Suppose the vehicle has a tendency to slip outward. Then the frictional force will be developed along the plane of road as shown in the figure. The frictional force can be divided into two components. Fcosθ (horizontal component) and F sinθ (vertical component).
From the figure are get N cosθ = F sinθ + mg
N cosθ – F sinθ = mg ………(1)
The component Nsinθ and Fsinθ provide centripetal force. Hence

![]()
Question 24.
The moment of intertial of a thin rod of mass M and length c about an axis perpendicular to the rod at its midpoint is \(\frac{\mathrm{Ml}^{2}}{12}\)
a) What is the radius of gyration in the above case?
b) A student has to find the moment of inertia of the above rod about an axis (AB) perpendicular to the rod and passing through one end of the rod. Name and state the law used for this case.
c) Using the theorem, find the moment of inertia of the rod about AB.
Answer:
a) \(\frac{m \ell^{2}}{12}\) = MK2
K = \(\frac{\ell}{\sqrt{12}}\)
b) Parallel axes theorem
c) I = I0 + Ma2
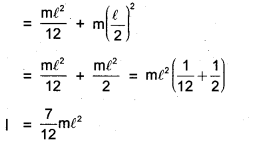
Question 25.
Small drops of water assumes spherical shape due to surface tension.
a) Define surface tension.
b) Derive an equation for the excess pressure inside a liquid drop of radius ‘R’ having surface tension‘σ’
c) Why do farmers plough the fields before summer?
Answer:
a) Liquid acquire a free surface when poured in a container. These surfaces posses some additional energy. This phenomenon is known as surface tension.
b) Consider a drop of liquid of radius r. Let pi and po be the values of pressure inside and outside the drop. Let the radius of liquid of drop increases by a small amount Dr under the pressure difference. The outward force acting on the surface of the drop,
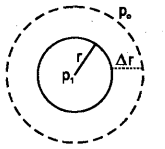
f = pressure difference × surface area,
ie. f = (pi – po)4pr2
If the radius of liquid drop is increased by Ar due to the above force
The workdone(ΔW) = f.Δr
= (pi – po)4pr2Δr ………..(1)
The increase in surface area of the drop
= 4p(r + Δr)2 – 4pr2
= 4p(r2 + 2rΔr + Δr2) – 4pr2 = 8prΔr
[ Neglecting Δr2]
If S is the surface tension of the liquid, the workdone to increase the surface area,
ΔW = Increase in surface area × surface tension
ΔW = 8prΔr.S ……..(2)
From equation (1) and (2), we get
Pi – Po = \(\frac{2 S}{r}\)
c) When the field is ploughed, capillaries are broken and hence water can not rise up and retains moisture.
Question 26.
Carnot engine is considered as an ideal heat engine.
a) Draw the P-V graph of Carnot’s cycle.
b) Derive an equation to find the work done during an adiabatic process.
c) Calculate the efficiency of a heat engine working between ice point and steam point.
Answer:
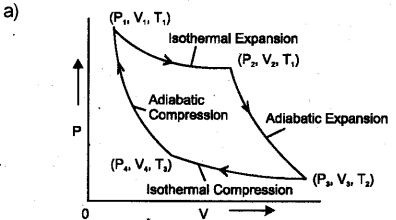
b) Let an ideal gas undergoes adiabatic charge from (P1, V1, T1) to (P2, V2, T2). The equation for adiabatic charge is pvγ = constant = k

