Kerala Plus One Physics Chapter Wise Questions and Answers Chapter 10 Mechanical Properties of Fluids
Plus One Physics Mechanical Properties of Fluids One Mark Questions and Answers
Question 1.
Water is flowing through a very narrow tube. The velocity of water below which the flow remains a streamline flow is known as
(a) relative velocity
(b) terminal velocity
(c) critical velocity
(d) particle velocity
Answer:
(c) critical velocity
Critical velocity is that velocity of liquid flow, upto which the flow of liquid is a streamlined and above which its flow becomes turbulent.
Question 2.
Bernoulli’s equation for steady, non-viscous, incompressible flow expresses the
(a) conservation of angular momentum
(b) conservation fo density
(c) conservation of momentum
(d) conservation of energy
Answer:
(d) conservation of energy
Question 3.
When cooking oil is heated in a frying pan, the oil moves around in the pan more easily when it is hot. The main reason for this is that with rise in temperature, there is a decrease in
(a) surface tension
(b) viscosity
(c) angle of contact
(d) density
Answer:
(d) density
Question 4.
At what temperature density of air is maximum?
Answer:
4°C
Question 5.
A thin glass plate is lying on a wet marble floor, It is difficult to pull the glass plate because of
(i) surface tension
(ii) Viscosity
(iii) friction
(iv) atmosphere
(v) Gravity
Answer:
(i) Viscosity
Question 6.
Why do clouds float in the sky?
Answer:
Zero terminal velocity
Question 7.
A spinning cricket ball does not follow parabolic path. Why?
Answer:
Due to the magnus effect.
Question 8.
The deepwater runs slow. Why?
Answer:
According to equation of continuity velocity is inversly proportional to velocity (AV = constant). Hence deep water runs slow.
Question 9.
Why dust generally settles down in closed room?
Answer:
The dust particles (tiny spheres) acquire terminal velocity as it fall through air. The terminal velocity is directly proportional to square of radius. Hence terminal velocity of dust particle is very small. So they settle down gradually.
Question 10.
Why more viscous oil is used in summer than in winter in scooters?
Answer:
The viscosity decreases with increase in temperature.
Question 11.
Why is sand drier than clay?
Answer:
Capillary action
Question 12.
Why cotton dress is preferred in summer?
Answer:
Cotton dresses have fine pores which act as capillaries for the sweat.
Question 13.
Why oil is poured to calm the sea?
Answer:
When oil is poured in water, the surface tension of water is reduced and water spreads over large area of sea.
Question 14.
How plants draw water from ground?
Answer:
The capillary action.
Question 15.
How do insects run on the surface of water?
Answer:
Because of surface tension, the surface of water behaves like stretched membrane hence it can support weight of small insects.
Question 16.
How ploughing a field helps to retain moisture?
Answer:
When field is ploughed, capillaries are broken and hence water can not rise up and retains moisture.
Question 17.
Hot soup tastes better than cold soup. Why?
Answer:
The surface tension of hot soap is less compared to cold soap. So hot soap spreads larger area.
Plus One Physics Mechanical Properties of Fluids Two Mark Questions and Answers
Question 1.
Remya found that a piece of metal weighs 210 g in air and 180 g when it is immersed in water. Determine the density of the metal piece.
Answer:
Relative density,
R.D = \(\frac{\text { Weight in air }}{\text { Loss of Weight in water }}\)
= \(\frac{210}{30}\) = 7.
Question 2.
Why is hot soup tastier than cold one?
Answer:
When temperature increases, the surface tension of soap decrease. Hence hot soap can enter into tiny pours of taste buds.
Question 3.
Why straws are used to drink soft drinks?
Answer:
When we suck the straw, pressure inside straw becomes lower than atmospheric pressure. This pressure difference cause the soft drink to rise through the straw.
Question 4.
Why new earthen pots keeps water cooler than old earthen pots?
Answer:
The capillaries of old earthen pots will get blocked with passage of time. For new earthen pots, water oozes out through capillaries, gets evaporated at the surface and makes it cool.
Plus One Physics Mechanical Properties of Fluids Three Mark Questions and Answers
Question 1.
Air is blown in between two pith balls suspended freely.
- What will happen to the balls?
- They repel each other
- They attract each other
- They start oscillating
- They remain in their initial position They fall on the ground
- Give your explanation
Answer:
- They attract each other
- When air is blown in between two pith balls, the pressure between the balls decreases. Due to this decrease in pressure between the balls, they attract each other.
Question 2.
A child dipped two identical capillary tubes, one in a beaker containing mercury. He observed that water and mercury have risen through the tubes to certain heights.
- Name this phenomenon.
- What difference did he observe in the shape of the meniscus of the two liquids in the tubes?
- If he plots a graph connecting the radius of the capillary tube and capillary height, what will be the shape of the graph?
Answer:
1. Capillary rise.
2. The shape of the water meniscus in the tube becomes concave upwards. But the shape of mercury measures in the tube become convex upward.
3. h α \(\frac{1}{r}\), this is in the form y α \(\frac{1}{x}\)
Hence when we draw graph between ‘h’ and ‘r’ we get a graph of hyperbola.
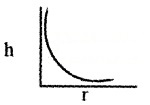
Question 3.
Bernoulli’s theorem is a consequence of energy conservation principle. Using this theorem explain the working of atomiser.
Answer:
Atomiser (application of Bernoulli’s theorem)
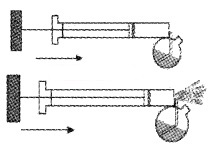
Atomizer is used for getting a fine spray of perfumer or insecticide. It consists of a cylinder with a piston. A small vessel containing liquid to be sprayed is attached to the cylinder. When the piston is moved forward air is blown out through a small opening of the cylinder.
As the velocity of flow of air increases, the pressure at the opening decreases. Due to the lower pressure at the opening, the liquid rises through the narrow tube and gets sprayed out along with air.
Question 4.
Surface tension is numerically equal to the surface energy.
- Difine surface tension.
- Derive an expression for the rise of liquid in a capillary tube.
Answer:
1. Liquids acquire a free surface when poured in a container. These surfaces possess some additional energy. This phenomenon is known as surface tension.
2. When a drop is split into tiny droplets, the surface area increases. So work has to be done for splitting the drop. Let R be radius of the drop and r the radius of the droplets: R = 1 × 10-3m
surface area of the drop = 4πR2
= 4π × (1 × 10-3)2
= 4π × 10-6m2
Volume of the drop = Volume of 106 droplets
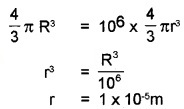
∴ Surface area of million droplets =106 × 4π2
= 106 × 4π(1 × 10-5)2
= 4π × 10-4 m2
∴ Increase in surface area = 4π × 10-4 – 4π × 10-6
= 3.96π × 10-4m2
∴ Energy expended = 3.967π × 10-4 × S
= 3.96π × 10-4 × 72 × 10-3J
= 8.95 × 10-5J.
Question 5.
Match the following
| 1. Pascal’s law | a. \( \sqrt{2 g h}\) |
| 2. Bernoulli’s theorem | b. a1v1= a2v2 |
| 3. Surface tension | c. Hydraulic jack |
| 4. Velocity of efflux | d. Reynolds number |
| 5. Equation of continuity | e. Angle of contact |
| 6. Viscosity | f. Ventiurimeter |
Answer:
1 – C, 2 – f, 3 – e, 4 – a, 5 – b, 6 – d.
Question 6.
Give reasons for the following cases.
- It is easier to swim in seawater than in river walls.
- The passangers are advised to remove ink from pen while going up in an aeroplane.
Answer:
1. The density of sea water is more than that of river water due to the presence of salt. Hence sea water offers more upthrust and only a very small portion of human body will be in seawater compared to river water.
2. In ink pen, ink is filled in atmospheric pressure. As we go higher pressure decreases and hence ink will have a tendancy to come out in order to equalise the pressure.
Plus One Physics Mechanical Properties of Fluids Four Mark Questions and Answers
Question 1.
A large tank containing water has a small hole near the bottom of the tank 1.5 m below the surface of water.
- What is the velocity of the water flowing from the hole?
- Explain the principle used in deriving the velocity of water flowing from the hole.
- Where must a second hole be drilled so that the velocity of water leaving this hole is half of water flowing through the first hole?
Answer:
1. Velocity of water flowing through the hole
u = \( \sqrt{2 g h}\)
= \(\sqrt{2 \times 10 \times 1.5}\) = 5.47m/s.
2. Bernoulli’s theorem
As we move along a streamline the sum of the pressure (p), the kinetic energy per unit volume \(\frac{\rho v^{2}}{2}\) and the potential energy per unit volume (ρgh) remains a constant.
(OR)
Mathematically Bernoulli’s theorem can be written as
P + \(\frac{1}{2}\)ρv2 + ρgh = constant.
3.
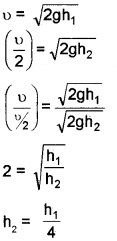
h2 = \(\frac{1.5}{4}\) m = 0.375 m, from the top side of tank.
Question 2.
Raindrops have an average size of 1 mm when it is formed at the upper atmosphere.
- Why the velocity of the raindrop is uniform?
- Derive an expression for the terminal velocity of the drop in terms of the coefficient of viscosity of air.
- If the size of the raindrop becomes half, then what happens to its terminal speed?
Answer:
1. Due to viscous force acting on the raindrop, it moves with uniform speed.
2. Viscous force, boyancy force and weight of the body
Expression for terminal velocity:
Consider a sphere of radius ‘a’ densitity σ falling through a liquid of density a and viscocity η. The viscous force acting on the sphere can be written as
F = 6πaηv
Where v is the velocity of sphere. This force is acting in upward direction. When the viscous force is equal to the weight of the body in the medium, the net force on the body is zero. It moves with a constant velocity called the terminal velocity.
The weight of a body in a medium,
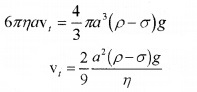
When body has terminal velocity, we can write.
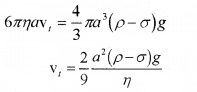
Question 3.
- Fill in the blanks using the word from the list appended with each statement.
- Viscosity of gases_____with temperature (increase/decrease)
- For a fluid in steady flow, the increase in flow speed at a constriction follows from_____ (conservation of mass/Bernoulli’s theorem)
- The working of a hydraulic lift is based on (Pascal’s Law/ principle of Conservation of Energy)
- Small insects can walk over the surface of water. It is due to the_____(surface tension of water/viscosity of water)
- A girl dips a thin capillary tube in water. Water rises through it.
- Name the phenomenon.
- How does this rise vary with the diameter of the tube?
Answer:
1. Fill in the blanks :
- increases
- Conservation of mass
- Pascals law
- Surface tension
2. A girl dips a thin capillary tube in water:
- Capillary rise
- h α \(\frac{1}{r}\) ie. when diameter of tube increases, the. capillary rise decreases.
Question 4.
The schematic diagram of a sprayer or atomiser is given below.
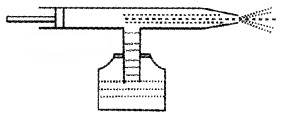
- Name the principle of working of this device from the following:
- Surface tension
- Viscosity
- Bernoulli’s principle
- Archimedes’ principle
- Write its mathematical expression.
- Wings of an aeroplane are curved outwards while flattened inwards. Why?
Answer:
1. Bernoulli’s principle
2. P + \(\frac{1}{2}\)ρv2 + ρgh = constant.
3. When the aeroplane moves forward, the air blown in the form of streamlines over the wings of aeroplane is shown in figure.
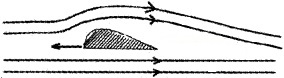
As the upper surface of wing is more curved than its lower surface, the speed of air above the wings is larger than the speed of the air below the wings.
Hence the pressure above the wings becomes less than the pressure below the wings. Due to this pressure difference the aeroplane will get upward force to overcome gravitational force.
Question 5.
During windstorms, roofs of certain houses are blown off without damaging other parts of the houses.
- Name the theorem which explains this phenomenon.
- State the theorem.
- Explain this phenomenon on the basis of this theorem.
Answer:
- Bernoulli’s theorem
- For a small amount of liquid in stream line flow, between two points, the total energy is constant.
- When windstorm blown off, the pressure on the top side of roof decreases. Hence a pressure difference is developed in between roof. Due to this pressure difference, roof of certain houses are blown off.
Question 6.
Two thin evacuated (one end closed) glass take A and B are carefully immersed in a beaker containing mercury such a way that there is no chance to get air in to the tubes. A is stand vertically and B is making an angle θ with the vertical.
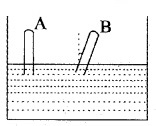
- Is any rise of mercury in the tubes?
- Is any height difference of mercury levels in tube A and B? Justify your answer.
- When the doctors are measuring body pressure, it is advisable to lie on a table. Why?
Answer:
- Yes
- No. Pressure is same at same level. To get same pressure, height of mercury becomes same.
- When we lie on the table, the pressure of our body will be same at all points.
Question 7.
A small metal sphere is falling through a caster oil.
- Name the forces acting on the metal sphere?
- Which of these forces change? Why?
- Name the velocity of the sphere when the unbalanced force on it is zero?
- Write down the expression for this velocity in terms of coefficient of viscosity?
Answer:
- forces acting on the metal sphere:
- Weight of the body (mg)
- Buoyant force or upthrust
- Viscous force
- Viscous force. Viscous force is the friction offered by the liquid. It is a self-adjusting force.
- Terminal velocity
- Terminal velocity, V = \(\frac{2}{9} a^{2}\left(\frac{f-N}{\eta}\right) g\).
Plus One Physics Mechanical Properties of Fluids Five Mark Questions and Answers
Question 1.
A capillary tube when dipped into water, it is commonly observed that water will rise through the tube.
- Which of the following is responsible for this?
- Gravitational force
- Viscous force
- Nuclear force
- Surface tension
- Elastic force
- Derive an expression for the capillary rise.
- If the radius of the tube becomes doubled, then what happens to the height of water column in the tube?
Answer:
1. Surface tension.
2.
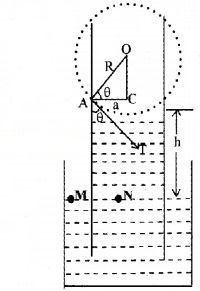
Consider a capillary tube of radius ‘a’ dipped in a liquid of density ρ and surface tension S. If the liquid has a concave meniscus it will rise in the capillary tube. Let h be the rise of the liquid in the tube. Let p1 be the pressure on the concave side of the meniscus and p0, that on the other side. The excess pressure on the concave side of the meniscus can be written as
p1 – p0 = \(\frac{2 \mathrm{S}}{\mathrm{R}}\)
Where R is the radius of the concave meniscus. The tangent to the meniscus at point A makes an angle θ with the wall of the tube.
In the right-angled triangle ACO
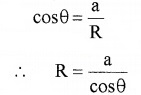
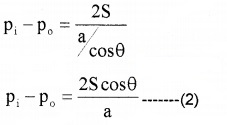
substituting the values of R in the equation (1)
Considering two points M and N in the same horizontal level of a liquid at rest,
the pressure at N = pressure at M
But the pressure at M = pi, the pressure over the concave meniscus, and pressure at N = po + hρg
∴ Pi = Po + hρg
or Pi – Po = hρg ……..(3)
From equations (2) and (3), we get
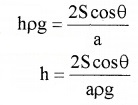
3. We know
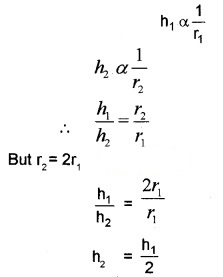
The capillary rise decreases to half of the original value.
Question 2.
- Find the odd one out and justify your answer Atomiser, venturi meter, aeroplane, hydraulic lift
- Mention one use of venturi meter.
- Explain the working of the odd one which you have selected in question (a)
Answer:
1. Hydraulic lift – It is based on pascals law.
2. Venturimeter can be used to find the velocity of flow of fluid through a pipe.
3.
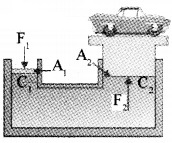
A hydraulic lift is used to lift heavy load. Consider a liquid enclosed in a vessel with two cylinders C1 and C2 attached as shown in the figure. The cylinders are provided with two pistons having areas A1 and A2 respectively.
If F1 is the force exerted on the area A1,
pressure P1 = \(\frac{F_{1}}{A_{1}}\).
If F2 is the force exerted on the area A2,
pressure P2 = \(\frac{F_{2}}{A_{2}}\).
According to pascal’s law P1 = P2.
Using this method we can lift heavy load by applying small force.
Question 3.
When a capillary tube of radius ‘r’ is dipped in water, the water rises through it up to height ‘h’.
- Which of the following is responsible for the above phenomenon?
- Viscous force
- elastic force
- surface tension
- gravitational force
- negative force
- To what height will water rise in a glass tube with a bore of radius 0.1 mm (take the angle of contact of glass with 0°, surface tension S = 0.0728 N/m)
- If the length of tube is less than the length of capillary rise, will it overflow? Justify your answer.
Answer:
1. Surface tension
2.

3. The water will never overflow. If the tube is of insufficient length, the radius of curvature of liquid meniscus goes on increasing, making it more and more flat till water is in equilibrium.
Question 4.
A steel ball of radius 1 mm is falling vertically through a tank of oil at 30°C.
- After some time the ball attains a constant velocity called_____
- What are the forces acting on the ball and give their directions?
- Write down the expression for resultant force acting on the ball?)
- If the density of oil is 2 × 103kg/m3, density of steel is 8 × 102 Kg/m3 and ‘η’of oil 2NS/m2, What will be the constant velocity attained by the ball?
Answer:
1. Terminal velocity.
2. Weight of body (down ward), bouyanant force (up ward), Viscous force (upward).
3. Resultant force = weight of body – buoyant force.
4. Terminal velocity,

Plus One Physics Mechanical Properties of Fluids NCERT Questions and Answers
Question 1.
A 50 kg girl wearing high heel shoes balances on a single heel. The heel is circular with a diameter 1.0 cm. What is the pressure exerted by the heel on the horizontal floor?
Answer:
Force, F = Weight of girl
= mg = 50 × 9.8N = 490N
Radius, r = 0.5 × 10-2m
Area A = πr2 = \(\frac{22}{7}\)(0.5 × 10-2)2 m2
Pressure

Question 2.
Torricelli’s barometer used mercury. Pascal duplicated it using French wine of density 984 kg m-3. Determine the height of the wine column for normal atmospheric pressure.
Answer:
p = hρg, h = \(\frac{p}{\rho g}=\frac{1.01 \times 10^{5}}{984 \times 9.8}\)m = 10.47m.
Question 3.
A U-tube contains water and methylated spirit separated by mercury. The mercury columns in the two arms are in level with 10.0 cm of water in one arm and 12.5 of spirit in the other. What is the specific gravity of spirit?
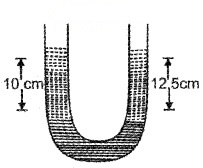
Answer:
Since the mercury columns in the two arms are at the same level,
∴ pressure due to water column = pressure due to spirit column
∴ hwρwg = hsρsg
or hwρw = hsρ
But hw = 10 cm,
ρw = 1 gcm-3,
hs = 12.5cm
∴ 10 × 1 = 12.5 × ρs
or ρs = \(\frac{10}{12.5}\)gcm-3
= 0.8cm-3
∴ Specific gravity of spirit = 0.8.
Question 4.
Figs, (a) and (b) refer to the steady flow of a non-viscous liquid. Which of the two figures is incorrect? Why?
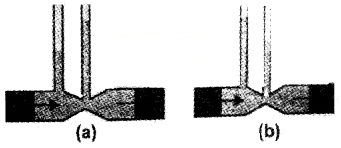
Answer:
Fig (a) is incorrect. This is because at a constriction (ie., where the area of cross-section of the tube is smaller), the flow speed is larger due to mass conservation. Consequently, pressure there is smaller according to Bernoulli’s equation. We assume the fluid to be incompressible.
Question 5.
What is the prssure inside the drop of mercury of radius 3.00 mm at room temperature? Surface tension of mercury at that temperature (20°C) is 4.65 × 10-1Nm-1. The atmospheric pressure is 1.01 × 105 Pa. Also give the excess pressure inside the drop.
Answer:
Excess pressure = \(\frac{2 \sigma}{R}\)
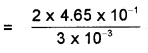
Total pressure = 1.01 × 105 + \(\frac{2 \sigma}{R}\)
= 1.01 × 105 + 310
= 1.0131 × 105Pa
Since data is correct upto three significant figures. We should write total pressure inside the drop as 1.1 × 105Pa.
Question 6.
During blood transfusion, the needle is inserted in a vein where the guage pressure is 2000 Pa, at what height must the blood container be placed so that blood may just enter the vein? Given: density of whole blood = 1.06 × 103kgm-3
Answer:
Guage pressure,
p = hρg, h
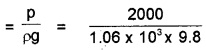
= 0.19m.