Kerala Plus One Physics Chapter Wise Previous Questions Chapter 2 Units and Measurement
Question 1.
Mechanical power is represented by P – F u + Av³p where, F is the force, v is the velocity, A is the area and ρ is the density. (MARCH – 2010)
a) The dimensional formula of power is……..
b) Check the dimensional validity of the above equation.
c) Which of the following equations can’t be obtained by the dimensional method?
i) \(\mathrm{T}=\mathrm{K} \sqrt{\ell / \mathrm{g}}\)
ii) E = k m v ²
iii) P = h ρ g
iv) N = N(o)e– λt
Answer:

This equation is correct.
c) N = N(o)e– λt
Question 2.
Give examples for the following : (MAY – 2010)
a) A dimensionless, unit less physical quantity.
b) A dimensionless physical quantity but having unit in SI system.
c) Two physical quantities which have the same dimensions.
Answer:
a) Relative density, relative permittivity, coefficient of friction.
b) Angle, or solid angle
c) Work – energy
Work – Torque
Question 3.
Pick out the fundamental unit from the following : Second, m/s, Newton, Joule. (MARCH – 2013)
Answer:
Second
Question 4.
Velocity of sound depends on density (ρ) and modulus of elasticity (E). (The dimensional formula of E is ML– 1T– 2. (MARCH – 2013)
a) State the principle of homogeneity.
b) Using the above principle, arrive at an expression for the velocity of sound. (Take K = 1)
Answer:
a) The dimension of the same fundamental quantity must be the same on either side of the equation.
b) The velocity of a sound through a medium may be assumed to depend on
i) the density (ρ) of medium modulus of elasticity (E)
i e, V ∝ ρa E b
V = K ρa Ea ………….
But K = 1
i e, V = ρa E b
Writing the dimensional formula of V, ρ and E We get
LT– 1 = [M L– 3]a [M L– 1 T– 2]b
M 0 L 1 T– 1 = Ma + b L– 3a – b T – 2b
Comparing the dimensions of M, L and T on the two sides, we get
a + b = 0 ………
– 3 a – b = 1 ………..(3)
and -2 b = -1 or b = 14
Substituting for b in eq (2)
a + 1/2 = 0
a = -1/2
Putting values of a and b in equation
V = ρ– 1/2 E 1/2
V = \(\sqrt{\frac{E}{\rho}}\)
Question 5.
The correctness of an equation is checked using the principle of homogeneity. (MAY – 2013)
Answer:
For an equation, x = a + bt + ct²; where x is in metre and t in second. What will be the dimension of ‘b’? According to principle of homogeneity, the dimensions of all the terms on the two sides of the equation are the same.
In this case,
x = b t
\(\mathrm{b}=\frac{\mathrm{X}}{\mathrm{t}}=\frac{\mathrm{L}}{\mathrm{T}}=\mathrm{LT}^{-1}\)
Question 6.
Significant figures determine the accuracy of the measurement of a physical quantity. (MAY – 2013)
a) The radius of a sphere is given by R = 1.03 m. How many significant figures are there in it?
b) If the percentage error in calculating the radius of the sphere is 2%, what will be the percentage error in calculating the volume?
Answer:
a) 3
b) Volume of sphere

Question 7.
Choose the correct alternative.
Gravitational force/weak nuclear force is the weakest fundamental force. (MARCH – 2014)
Answer:
Gravitational force is the weakest fundamental force.
Question 8.
The centripetal force on a body in circular motion is given by F = \(\frac{m v^{2}}{r}\) (MARCH – 2014)
a) Write the dimension of force.
b) Using the above formula, write an equation to find % error in centripetal force.
c) What is the number of significant figures in 0.050 N?
Answer:
a) F = M.LT– 2
b) F = \(\frac{m v^{2}}{r}\)
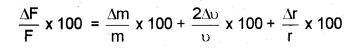
c) 2
Question 9.
Dimensional method helps in converting the units from one system into another. (MAY – 2014)
a) Name the principle used for the above purpose.
b) Using dimension, prove 1 Newton = 105 dynes.
Answer:
a) The principle of homogenity.
b) Dyne is the unit of force in the C.G.S. system . and newton is the S.I.unit. The dimensional formula for force is M 1 L 1 T– 2.
Here, a=1, b=1 and c=2.

Question 10.
a) Suggest a method to measure the diameter of the Moon. (MARCH – 2015)
b) Length, breadth and thickness of a block is measured using vernier calipers. The percentage errors in the measurements are 2%, 1% and 3% respectively. Estimate the percentage error in its volume.
c) A physical quantity is given by h =\(\frac{\mathrm{Fv}^{2}}{\mathrm{~L}}\) F is the force, v is the velocity and L is the angular momentum. Find the dimensions of h.
Answer:
a) Parallax method
b) v = l b t
Percentage error in volume,
![]()
= 2% + 1% + 3% = 6%
c)

Question 11.
The correctness of equations can be checked using the principle of homogeneity. (MAY – 2015)
a) State the principle of homogeneity.
b) Using this principle, check whether the following equation is dimensionally correct.
![]()
where m is the mass of the body, u is its velocity, g is the acceleration due to gravity and h is the height.
c) If percentage errors of measurement in velocity and mass are 2% and 4% respectively, what is the percentage error in kinetic energy?
Answer:
a) In an equation containing more than two terms, the dimensions of each term must be the same.
b) Dimension of (1/2 m v 2) = M x (LT– 1)2 = M L 2 T – 2
Dimension of (m g h) = M x (LT– 2) x L= M L 2 T – 2
The dimension is same on either side of the equation. Hence equation is dimensionally correct.
c)
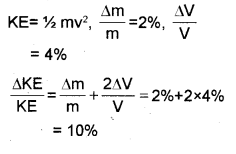
Question 12.
a) The error in the measurement of radius of a circle is 0.6%. Find the percentage error in the calculation of the area of the circle. (MARCH – 2016)
b) Name the principle used to check the correctness of an equation.
c) What is the number of significant figures in 0.00820 J?
Answer:
a)
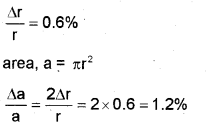
b) The principle of homogeneity
c) 3
Question 13.
a) Length of a sheet is 17.3 ± 0.3 cm and breadth is 3.12 ± 0.08 cm. Calculate the percentage error in the area. (MAY – 2016)
b) Using the principle of homogeneity of equations,
check whether the equation is correct. T = \(\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{g}}{\mathrm{l}}}\)
(T -> time, g -> acceleration, l -> length)
Answer:
a) Area, A = l x b

The dimension of T is not equal to dimension of \(\sqrt{g / l}\) Hence the equation is wrong.
Question 14.
a) Figure below shows the parallax method’ to measure the distance ‘D’ of a planet ‘S’ from the earth (MARCH – 2017)
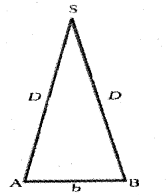
Mark the parallax angle θ in the figure. Explain how the distance ‘D’ can be measured.
b) Check whether the equation m v ² = m g h is
Answer:
a) Parallax method is used to find distance of planet or star from earth.
The distance between two points of observation (observatories) is called base. The angle between two directions of observation at the two points is called parallax angle or parallactic angle (θ).
Parallax Method
The planet ‘s’ is at a distance ‘D’ from the surface of earth. To mea-sure D, the planet is observed from two observatories A and B (on earth). The distance between A and B is b and 0 be the parallax angle between direction of observation from A and B.
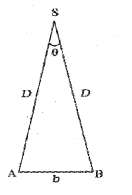
AB can be considered as an arch of length ‘b’ of a circle of radius D with its center at S. (Because b θ is very small, \(\frac { b }{ D}\)<<1 ] Thus from arch-radius relation
θ = \(\frac { b }{ D}\)
D = \(\frac { b }{ θ}\)
Thus by measuring b and 0 distance to planet can be determined.
b) dimension of m = M
dimension of h = L
dimension of v = LT – 1
dimension of g = LT– 2
dimension of m v 2 = M x (LT– 1) = ML 2 T– 2
dimension of m g h = M x LT– 2 x L
= M L 2 T – 2
dimension of LHS = dimension of RHS
Hence equation is dimensionally consistent.
A dimensionally correct equation need not be actually an exact equation. I do agree with the statement. Eventhough the equation m v 2 = m g h is dimensionally correct, the exact equation is \(\frac { 1 }{ 2 }\)m v 2= m g h. This is a drawback of dimensional analysis.
Question 15.
A company manufacturing PVC pipes claims in an advertisement that the volume of water flowing out through the pipe in a given time is as per the equation V = K A 2 u t where A is the area of cross section of the pipe, u is the speed of flow, t is the time and K is a dimensionless constant. (MAY – 2010)
a) Name the principle that can be used to check the dimensional correctness of this equation.
b) Check the equation and state whether the claim is correct.
Answer:
a) Principle of homogenity
b) V = K A 2 u t
L 3 = (L 2)2 x LT – 1 T
L 3 ≠ L 5
The claim is not correct.
Question 16.
a) A student was asked to write the equation for displacement at any instant in a simple harmonic motion of amplitude ‘a’. He wrote the equation as (MARCH – 2011)
\(\mathrm{y}=\mathrm{a} \sin \frac{2 \pi \mathrm{v}}{\mathrm{k}} \mathrm{t}\)
Where ‘v’ is the velocity at instant T. For the equation to be dimensionally correct, what should be the dimensions of k ?
b) What is the area of a square of side 1.4 cm in proper significant figures?
Answer:
a) K = L
b) Area = (1.4 x 1.4) cm 2
= 1.96 cm 2
= 2.0 cm 2
Question 17.
To measure distance we use different units. Which of the following is the largest unit of length? (MAY – 2011)
a) Kilometer
b) Astronomical unit
c) Light year
d) Parsec
Answer:
d) Parsec
Question 18.
Which of the following measurement is more accurate? Why? (MAY – 2011)
i) 500.00 kg.
ii) 0.0005 kg.
iii) 6.00 kg.
Answer:
500.00 kg is more accurate because it contain more significant figures.
Question 19.
All Physical quantities can be expressed in terms of dimension. (MARCH – 2012)
a) Write the physical quantities of the following dimensions:
i) [M 1 L 1 T – 1]
ii) [M 1L 2T – 2]
b) Check whether the equation
T = \(2 \pi \sqrt{\frac{m}{g}}\) is dimensionally correct.
T -> Time period of a simple pendulum
m-> mass of the bob
g -> acceleration due to gravity
Answer:
a) i) Momentum or impulse .
ii) Work, energy, torque
b)
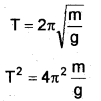
Taking dimensions on both sides,
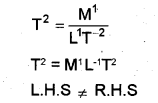
So the equation is wrong.
Question 20.
a) Which measurement is most precise? (MAY – 2012)
i) Vernier Calipers having 5 divisions on sliding scale
ii) Vernier Calipers having 10 divisions on sliding scale.
iii) Vernier Calipers having 20 divisions on sliding scale.
b) What happens to the accuracy when the least count is decreased?
Answer:
a) Vernier calipers having 20 divisions on sliding scale.
b) Accuracy increases.
Question 21.
a) A boy recalls the relativistic mass wrongly as (MAY – 2012)
![]()
Using dimensional method put the missing ‘C’ at proper place.
b) Name and state the principle used in solving the above problem.
Answer:
By the principle of homogenity of dimension [m] = [m0]
So \(\sqrt{1-v^{2}}\) must be dimensionless
for that \(\sqrt{1-v^{2} / c^{2}}\) is the correct form.
b) Principle of homogenity of dimension.
According to this principle, the dimensions of the fundamental quantities (mass, length and time) are same in each and every term on either side of the physical relation