Plus One Physics Chapter Wise Previous Questions Chapter 15 Waves

Kerala Plus One Physics Chapter Wise Previous Questions Chapter 15 Waves

Question 1.
Nobody can imagine a world without sound. Sound is a part of our life  musics, ripples, echoes etc. have a lot of applications. [March – 2010]
(a) Can you say how a bat can ascertain directions and distances without any eyes’?
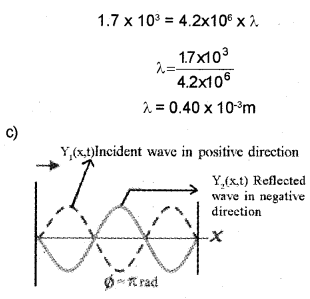
(b) Doctors use an ultrasonic scanner to diagnose tumour tissues. If the frequency of the scanner is 4.2 MHz and the speed of sound wave in the tissue is 1.7 kms, find the wavelength of the sound wave.
(c) Obtain the equation of a standing wave. Then plot it to locate the nodal and antinodal points.
Answer:
(a) Bats can produce ultrasonic sounds. The ultra-sonic sounds reflected from the object helps to identify direction and distance.
(b) Velocity of sound, v = μλ.

When two waves of same amplitude and fre­quency travelling in opposite direction superim­pose the resulting wave pattern does not move to either sides. This pattern is called standing wave. The wave travelling in positive direction of x – axis
y₁(x,t) = a sin(kx-ωt)
The wave travelling in negative direction of x-axis
y₂(x,t) = a sin(kx + ωt)
According to superposition Principle, the combined wave is
y(x,t) ⇒ -y₁(x,t) +y₂(x,t)
y(x,t) = a sin(kx-ωt)+a sin(kx + ωt)
Hence we get,combined wave as
y(x,t) = 2a sin(kx) x cosωt
This wave has an amplitude of ‘ 2 a sinkx and it is not a moving wave.

Nodes & Antinodes

The position of maximum amplitude in a stand­ing wave is termed as anti node and position of minimum amplitude (zero) is termed as node.

Node:
The amplitude of standing wave is ‘2a sinkx ’. It is zero
when kx = 0, π,2π…. etc.
i..e kx = nπ.

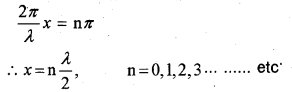
Antinode:
The amplitude has maximum value 2a when (2a sin kx = 2a)

Question 2.
A flute is an example of an open pipe. [May – 2010]
(a) Sketch the pattern of wave forms of the first two harmonics formed in an open pipe.
(b) Show that in an open pipe the frequencies of the first 3 harmonics are in the ratio 1:2:3.
Answer:

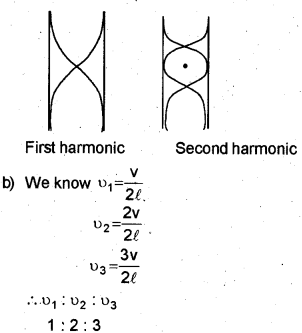
Question 3.
(a) Wave motion is a propagation of energy through a material medium due to repeated periodic motion.
(i) Transverse waves cannot be propagated through gases. Why? [May -2011]
(ii) What was the condition assumed by Laplace in correcting Newton’s equation for the veloc­ity of sound in a gas? Write the Newton- Laplace equation.
(b) A source of sound of frequency 256 Hz is in between a listener and a wall. If the source is moving towards the wall with a velocity of 5 ms^-1 how many beats per second will be heard if the sound travels with a speed of 330 ms^-1?
Answer:
(a)

• Modulus of eleasticity of gas is zero
• Laplace corrected Newtons formula taking condensation and rare fraction as adiabatic process.

Question 4.
In a laboratory Raju uses a tuning fork in resonance column experiment. [March-2011]
(a) What type of wave is produced by the tuning fork . in the case?
(b) Mention any four characteristics of these waves.
Answer:
(a) Longitudinal wave
(b) Properties of longitudinal wave

• The direction of vibration of particles is perpen- dicularto direction of propagation of wave.
• They travel in the form of condensations and rare fractions.

Question 5.
Fill in the blanks:

Answer:

Question 6.
While conducting a resonance column experiment in the laboratory, you can hearthe maximum sound at a certain height. [March – 2012]
(a) Explain the phenomenon of sound.
(b) Show that in a closed pipe at one end, the fre­quencies of the first three harmonics are in the ratio of o,: u₂:u₃: = 1 : 3 : 5.
(c) Open pipes are preferred to closed ones in musi­cal instruments. Why?
Answer:
(a) If a wave is produced at the open end of a tube it travels through the gas column and gets reflected at the closed end. At a certain height of tube the incident wave and reflected wave superpose each other and produce stationary wave and a sound is heared. This is called resonance. The open end always represents an antinods.

(b) In a closed pipe, antinode is formed at open end. If L is the length of pipe.
\(x=(n+1 / 2) \lambda / 2, n=0,1,2 \ldots \text { etc }\)

(c) All harmonics are present in open pipe. (But only odd harmonics are present in closed pipe). Due to the presence of all harmonics in open pipe, it is preferred in musical instruments.

Question 7.
A transverse harmonic wave on a string is described by y (x, t) = 3.0 sin (36t + 0.018x + \(\frac{\pi}{4}\)) where x and y are in centimeters and t in seconds. The positive direction of x is from left to right. [May – 2012]
(a) Is it a travelling or stationary wave?
(b) What are its amplitude and frequency?
(c) What is the initial phase at the origin?
(d) If it is a travelling wave, what are the speed and direction of its propagation?
Answer:
(a) Travelling or progressive wave.
(b) Comparing y(x, t) = 3 Sin (36t + 0.018x + \(\frac{\pi}{4}\)) with
standard equation y(x, t) = A Sin (ωt + kx + φ)
We get amplitude A = 3 cm

Question 8.
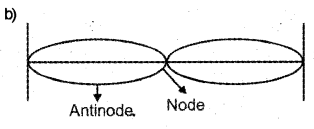
A student plucks at the center of a stretched string and observes the wave pattern produced. [March – 2013]

1. What type of wave is produced in the string?
2. Plot the above wave pattern pictorially. Label the nodes and the antinodes on the pattern.

Answer:
(a) Standard Wave

Question 9.
A sound travelling along a string is described by y = 0.005 Sin (80.0 x-3.0t). [May – 2013]
(a) Calculate:

1. Amplitude (1)
2. Wavelength (1)

(b) Where will a man hear a louder sound in the case of stationary wave (node or antinode)? Why?
Answer:
The equation for sound wave is given as
y = 0.005 sin (80.0x – 3.0t)
Comparing with standard equation for wave motion
y = a sin (kx – ωt) we get
Amplitude a = 0.005m
Similarly, kx = 80.0x
k = 80
\(\begin{aligned}
\frac{2 \pi}{\lambda} &=80 \\
\lambda &=\frac{2 \pi}{80} \mathrm{~m}
\end{aligned}\)

(b) At antinode
The amplitude of oscillation is more at antinode. Hence we hear a louder sound at antinode.

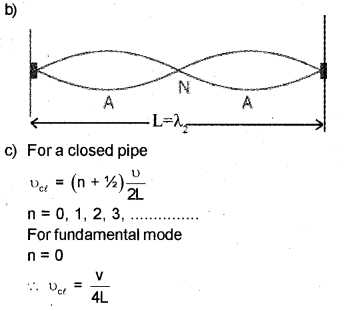
Question 10.
The equation for a wave is given below. [March -2014]
y = Asin(kx +ωt)
(a) Is it a travelling or stationary wave
(b) Draw the stationary waves in a stretched string in the second harmonic.
(c) Show that the fundamental frequency of an open pipe is twice the fundamental frequency of a closed pipe of the same length.
Answer:
(a) Travelling Wave

Question 11.
A transverse harmonic wave on a string is described by y(x, t) = 3.0 Sin(36t + 0.018 + \(\frac{\pi}{4}\)) Where x and y are in centimeters and t in seconds. The positive direction of x is from left to right. [May – 2014]
(a) Is this a travelling wave ora stationary wave?
(b) If it is travelling, what is the speed and direction of its propagaiton?
(c) What is its amplitude and frequency
(d) What is the initial phase at the origin?
Answer:
(a) Travelling wave
(b) Generally the wave propogating in negative x-di- rection is given by y (x,t) = a sin (kx +wt + \(\frac{\pi}{4}\))

Comparing the above with given equation y (x, t) = 3.0 sin (0.018x + 36t + \(\frac{\pi}{4}\))
We get k = 0.018m^-1 and w = 36 rad/s

Question 12.
While performing the resonance column apparatus experiment in a laboratory at a certain height, you can hear maximum sound. [March – 2015]
(a) Name the physical concept behind it.
(b) Explain with diagrams,the normal modes of vi­bration in the case of air in an open tube.
(c) Open pipes are preferred to closed one in musi­cal instruments. Why?

• Resonance
• In open tube, both ends are open. At both ends, antinodes are formed.

(c) In an open pipe all harmonics are generated in closed pi pie only odd harmonics are generated. So open pipes are preferred in musical instruments.

Question 13.
The pitch of the siren of a fire engine increases as it approaches a boy standing at a bus stop. [May – 2015]
(a) The phenomenon behind it, is due to …

• Doppler effect
• Standing wave
• Newtons law of cooling
• Resonance

(b) Obtain a general expression for the apparent frequency of the siren as heard by the boy.
Answer:
(a) (i) Doppler effect

(b) The apparent change in the frequency of sound wave due to the relative motion of source or lis­tener or both is called Doppler effect. It was pro­posed by John Christian Doppler and it was ex­perimentally tested by Buys Ballot.

Considers source is producing sound of frequency v. Let V be the velocity of sound in the medium and λ the wavelength of sound when the source and the listener are at rest

The frequency of sound heard by the listener is v
\(v=\frac{v}{\lambda}\)

Let the source and listener be moving with veloci­ties v_s and v_l in the direction of propogation of sound from source to listener. (The direction S to L is taken as positive)
The relative velocity of sound wave with respect to the source = V – V_s
Apparent wavelength of sound,
\(\lambda^{1}=\frac{V-V_{s}}{v} \ldots \ldots \cdots ….(1)\)

Since the listener is moving with velocity v_l, the relative velocity of sound with respect to the lis­tener,
\(\mathrm{V}^{1}=\mathrm{V}-\mathrm{V}_{\ell} \ldots \ldots \ldots . .(2)\)

Apparent frequency of sound as heard by the lis­tener is given by
\(v^{1}=\frac{v^{1}}{\lambda^{1}}\ldots \ldots \ldots . .(3)\)

Sub (1) and (2) in eq.(3) we get
\(\begin{aligned}
v^{1} &=\frac{V-V_{\ell}}{\frac{V-V_{s}}{v}} \\
v^{1} &=v\left(\frac{V-V_{e}}{V-V_{s}}\right)
\end{aligned}\)

Question 14.
In resonance column experiment, we can hear maximum sound at a certain height. This is due to the phenomenon of resonance. [March – 2016]
(a) Show that for a pipe closed at one end, the frequencies are in the ratio υ₁: υ₂: υ₃ = 1:3:5.
(b) Open pipes are preferred to closed pipes in musical instruments. Why?
Answer:
(a) In a closed pipe, antinode is formed at open end. If L is the length of pipe.
\(x=(n+1 / 2) \lambda / 2, n=0,1,2 \ldots \text { etc }\)

(b) In closed pipe, only odd harmonics are gener­ated. In open pipe both even and odd harmonics are generated. Hence open pipes are preferred to closed pipes in musical instruments.

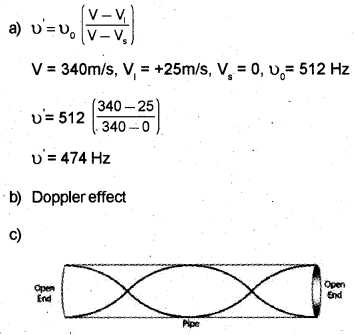
Question 15.
A woman is travelling in a car at a speed of 25m/s. She is moving away from a source producing a sound of 512 Hz.
(a) Calculate the frequency of sound heard by her. (Speed of sound in air = 340 m/s) [March – 2016] 
(b) Name the phenomenon that explains this variation infrequency.
(c) Draw the second harmonic of an open pipe (both end open). Mark a node and an antinode in the figure.
Answer:

Question 16.
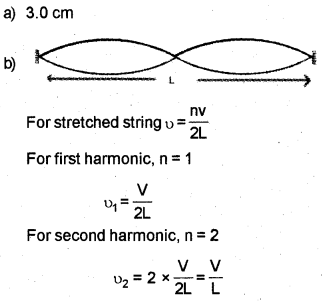
(a) A transverse harmonic wave is described by y = 3.0 sin (0.018x+ 36t), where ‘x’ and ‘y’ are in cm. The amplitude of this wave is  ……. (1)   [March – 2017]   
(b) Figure below shows the fundamental mode or first harmonic in a stretched string, when a standing wave is formed in the string.

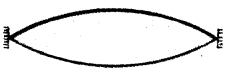
Draw the figure that shows the second harmonic in the string. If ‘L’ is the length of the string and V is the speed of the wave in the string, what are the equations of first and second harmonic fre­quencies?
Answer:

Plus One Physics Chapter Wise Previous Questions