Plus One Maths Notes Chapter 1 Sets is part of Plus One Maths Notes. Here we have given Kerala Plus One Maths Notes Chapter 1 Sets.
| Board | SCERT, Kerala |
| Text Book | NCERT Based |
| Class | Plus One |
| Subject | Maths Notes |
| Chapter | Chapter 1 |
| Chapter Name | Sets |
| Category | Plus One Kerala |
Kerala Plus One Maths Notes Chapter 1 Sets
I. Sets
Set is a well-defined collection of distinct objects.
Examples of sets.
- N: Set of Natural numbers.
- Z: Set of Integers.
- Q: Set of Rational numbers.
- R: Set of Real numbers.
- Z+: Set of Positive Integers numbers.
- Q+: Set of Positive Rational numbers.
- R+: Set of Positive Real numbers.
Representation of Sets:
- Roster Form: All elements are listed, are separated by commas, and closed using brackets.
- Set-builder Form: All elements of a set possess a single common property which is not possessed by any elements outside the set.
- Venn Diagram: Here sets are represented by diagrams. These diagrams consist of rectangles and closed curves usually circles. The universal et is represented by a rectangle and its subsets by circles.
II. Types of Sets:
Empty set: Set contains no element, φ or {}.
Singleton set: Set containing one element.
Finite set: Set containing a definite number of elements.
Infinite set: Set containing an infinite number of elements..
Equivalent set: Sets containing an equal number of elements.
Equal set: Sets containing identical elements.
Subset: If every element of A is an element of B, denoted by A ⊂ B. For any set A, the set A and Empty set is a subset of A. If a set A has n elements, then it has 2n subsets.
Superset: B is a superset if A is a subset of B, denoted by B ⊃ A.
Proper Subset: If A ⊂ B and A ≠ B.
Power set: The set of all subsets of a set A, denoted by P(A). If n(A) = n, then n(P(A)) = 2n
Universal set: The superset of all subsets under discussion.
Intervals as subset of R:
- [a, b] = {x : a ≤ x ≤ b}, closed interval.
- (a, b] = {x : a < x ≤ b]
- [a, b) = {x : a ≤ x < b}
- (a, b) = {x : a < x < b}, open interval.
III. Operations on Sets
Union of Sets: The union of A and B is the set which consists of all elements of A and all elements of B except the common elements. In symbol we write as A ∪ B = {x : x ∈ A or x ∈ B}.
Venn diagram representation:
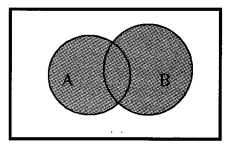
Properties:
- A ∪ B = B ∪ A, Commutative.
- (A ∪ B) ∪ C = A ∪ (B ∪ C), Associative
- A ∪ φ = A, φ is the identity.
- A ∪ A = A
- U ∪ A = U
Intersection of Sets: The intersection of A and B is the set of common elements of both A and B.
In symbol, we write as A ∩ B = {x : x ∈ A and x ∈B}.
Venn diagram representation:
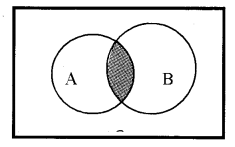
Properties:
- A ∩ B = B ∩ A, Commutative.
- (A ∩ B) ∩ C = A ∩ (B ∩ C), Associative
- A ∩φ = φ
- A ∩ A = A
- U ∩ A = A
- A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
- n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
- If A and B are disjoint, then n(A ∪ B) = n(A) + n(B)
- n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(C ∩ A) + n(A ∩ B ∩ C)
Difference of Sets: The difference of the sets A and B in this order is the set of elements which belongs to A but not to B, denoted by A – B = {x : x ∈ A and x ∉ B}
Venn diagram representation:
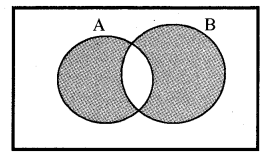
Property: A – B ≠ B – A
Complement of a Set: The complement of a set A is the set of all elements of U which are not in A, denoted by
A’ = {x : x ∈ U and x ∉ A}
Venn diagram representation:
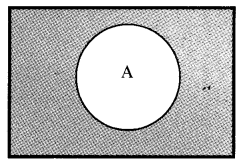
Properties:
- A’ ∪ A = U, Commutative.
- A’ ∩ A = φ, Associative
- (A ∩ B)’ = A’ ∪ B’
- (A ∪ B)’ = A’ ∩ B’
- U’ = φ
- φ’ = U
- (A)’ = A
- A – B = A ∩ B’
- n(A – B) = n(A ∩ B’)
- n(A) = n(A ∩ B’) + n(A ∩ B)
- n(A ∪ B) = n(A ∩ B’) + n(A’ ∩ B) + n(A ∩ B)
We hope the Plus One Maths Notes Chapter 1 Sets help you. If you have any query regarding Kerala Plus One Maths Notes Chapter 1 Sets, drop a comment below and we will get back to you at the earliest.