Plus One Maths Chapter Wise Questions and Answers Chapter 11 Conic Sections

Kerala Plus One Maths Chapter Wise Questions and Answers Chapter 11 Conic Sections

Plus One Maths Conic Sections Three Mark Questions and Answers

Question 1.
Find the coordinate of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse. (3 score each)

1. \(\frac{x^{2}}{4}+\frac{y^{2}}{25}\) = 1
2. \(\frac{x^{2}}{16}+\frac{y^{2}}{9}\) = 1

Answer:
1. Since 25 > 4 the standard equation of the ellipse is \(\frac{x^{2}}{b^{2}}+\frac{y^{2}}{a^{2}}\) = 1 ⇒ a² = 25; b² = 4
c² = a² – b² = 25 – 4 = 21 ⇒ c = \(\sqrt{21}\)
Coordinate of foci are (0, ±\(\sqrt{21}\))
Coordinate of vertex are (0, ±5)
Length of major axis = 2a = 2 × 5 = 10
Length of minor axis = 2b = 2 × 2 = 4
Eccentricity = e = \(\frac{c}{a}=\frac{\sqrt{21}}{5}\)
Length of latus rectum = \(\frac{2 b^{2}}{a}=\frac{2 \times 4}{5}=\frac{8}{5}\).

2. Since 16 > 9 the standard equation of the ellipse is \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 ⇒ a² = 16; b² = 9
c² = a² – b² = 16 – 9 = 7 ⇒ c = \(\sqrt{7}\)
Coordinate of foci are (±\(\sqrt{7}\), 0)
Coordinate of vertex are (±4, 0)
Length of major axis = 2a = 2 × 4 = 8
Length of minor axis = 2b = 2 × 3 = 6
Eccentricity = e = \(\frac{c}{a}=\frac{\sqrt{7}}{4}\)
Length of latus rectum = \(\frac{2 b^{2}}{a}=\frac{2 \times 9}{4}=\frac{9}{2}\).

Question 2.
Find the ellipse satisfying the following conditions: (3 score each)

1. Vertex (±5, 0); foci (±4, 0)
2. Ends of the major axis (±3, 0), ends of minor axis (0, ±2)
3. Length of the major axis 26, foci (±5, 0)
4. b = 3, c = 4, centre at origin; foci on the x-axis

Answer:
1. Foci (±4, 0) lie on the x-axis. So the equation of the ellipse is of the form \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1
Given; Vertex (±5, 0) ⇒ a = 5
Given; Foci(±4, 0) Foci ⇒ c = 4 = \(\sqrt{a^{2}-b^{2}}\)
⇒ 4 = \(\sqrt{25-b^{2}}\) ⇒ 16 = 25 – b² ⇒ b² = 9
Therefore the equation of the ellipse is
\(\frac{x^{2}}{25}+\frac{y^{2}}{9}=1\).

2. The ends of major axis lie on the x-axis. So the equation of the ellipse is of the form
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1
Given; Ends of the major
axis (±3, 0) ⇒ a = 3, ends of minor axis
(0, ±2) ⇒ b = 2
Therefore the equation of the ellipse is
\(\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\).

3. Since foci (±5, 0) lie on x-axis, the standard form of ellipse is \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1
Given; 2a = 26 ⇒ a = 13
Given; c = 5 = \(\sqrt{a^{2}-b^{2}}\)
⇒ 25 = 169 – b² ⇒ b² = 144
Therefore the equation of the ellipse is
\(\frac{x^{2}}{169}+\frac{y^{2}}{144}=1\).

4. The standard form of ellipse is
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1
Given; c = 4 = \(\sqrt{a^{2}-b^{2}}\)
⇒ 16 = a² – 9 ⇒ a² =25
Therefore the equation of the ellipse is
\(\frac{x^{2}}{25}+\frac{y^{2}}{9}=1\).

Question 3.
Find the coordinates of foci, the vertices, eccentricity and the length of latus rectum of the following hyperbolas. (3 score each)

1. \(\frac{y^{2}}{9}-\frac{x^{2}}{27}=1\)
2. 5y² – 9x² = 36

Answer:
1. The equation of the hyperbola is of the form
\(\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\) ⇒ a² = 9; b² = 27
⇒ c² = a² + b² ⇒ c² = 9 + 27 = 36 ⇒ c = 6
Coordinate of foci are (0, ±6)
Coordinate of vertices are (0, ±a) ⇒ (0, ±3)
Eccentricity = \(\frac{c}{a}=\frac{6}{3}=2\)
Length of latus rectum = \(\frac{2 b^{2}}{a}=\frac{2 \times 27}{3}=18\).

2. Given; 5y² – 9x² = 36


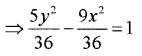
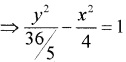
The equation of the hyperbola is of the form

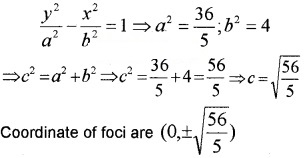
Coordinate of vertices are

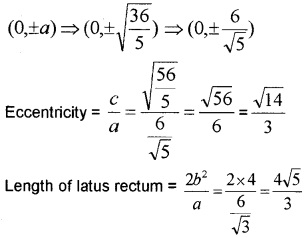
Question 4.
Find the hyperbola satisfying the following conditions: (3 score each)

1. Vertices (+2, 0), foci (±3, 0)
2. Foci (±5, 0), the transverse axis is of length 8.
3. Foci(0, ±13), the conjugate axis is of length 24.
4. Foci (±3\(\sqrt{5}\), 0), the latus rectum is of length 8.
5. Vertices (±7, 0) , e = \(\frac{4}{3}\).

Answer:
1. Since Vertices are (±2, 0) the standard form of hyperbola is

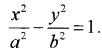
⇒ a = 2
Given; foci (±3, 0) ⇒ c = 3
⇒ c² = a² + b² ⇒ 9 = 4 + b² ⇒ b² = 5
The equation of the hyperbola;

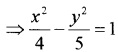
2. Since Foci are (±5,0) the standard form of hyperbola is

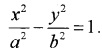
⇒ c = 5
Given; the transverse axis is of length 8.
⇒ 2a = 8 ⇒ a = 4
⇒ c² = a² + b² ⇒ 25 = 16 + b² ⇒ b² = 9
The equation of the hyperbola;

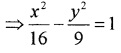
3. Since Foci are(0, ±13)the standard form of hyperbola is

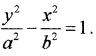
⇒ c = 13
Given; the conjugate axis is of length 24.
⇒ 2b = 24 ⇒ b = 12
⇒ c² = a² + b² ⇒ 169 = a² + 144 ⇒ a² = 25.
The equation of the hyperbola;

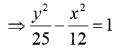
4. Since Foci are(±3\(\sqrt{5}\), 0) the standard form of hyperbola is

⇒ c = 3\(\sqrt{5}\)
Given; the latus rectum is of length 8.
⇒ \(\frac{2 b^{2}}{a}\) = 8 ⇒ b² = 4a
⇒ c² = a² + b²
⇒ 45 = a² + 4a ⇒ a² + 4a – 45 = 0
⇒ (a + 9)(a – 5) = 0 ⇒ a = -9, 5
a = -9 is not possible
⇒ a = 5 ⇒ b² = 20
The equation of the hyperbola;

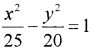
5. Since Vertices are (±7, 0) the standard form of hyperbola is

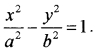
⇒ a = 7
Given;

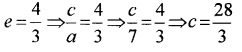
⇒ c² = a² + b²

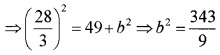
The equation of the hyperbola;

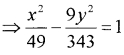
Question 5.
The line x – 1 = 0 is the directrix of a parabola, y² = kx then

1. Find the value of k. (1)
2. Find the vertex, focus, axis of parabola and length of latus rectum of the parabola. (3)

Answer:
1. Given directrix x – 1 = 0, so a = 1, then the equation of the parabola is
y² = -4ax ⇒ y² = -4x
Hence k = – 4

2. Vertex is (0, 0)
Focus of SS’ = (-1, 0)
Length of latus rectum = 4 × 1 = 4.

Question 6.
In the figure S and S’ are foci of the ellipse, \(\frac{x^{2}}{25}+\frac{y^{2}}{16}=1\) and P is a viable point on the ellipse.

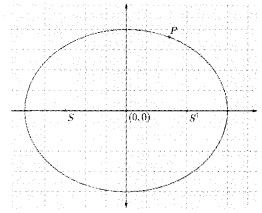
1. Find the co-ordinate of foci. (2)
2. Find the distance between S and S1. (1)
3. What is the maximum area of the triangle PSS’. (1)

Answer:
1. Since 25 > 16 the standard equation of the ellipse is \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1
⇒ a² = 25; b² = 16
c² = a² – b² = 25 – 16 = 9 ⇒ c = 3
Coordinate of foci are (±3, 0).

2. Distance between the two focus is 3 + 3 = 6.

3. Maximum area is attained when the point P reaches the point the ellipse meet the y
axis. Then area is = \(\frac{1}{2}\) × 6 × 4 = 12.

Plus One Maths Conic Sections Four Mark Questions and Answers

Question 1.
Find the equation of the circle passing through the points (4, 1) and (6, 5) and whose centre is on the line 4x + y = 16.
Answer:
Let the equation of the circle be
x² + y² + 2gx + 2fy + c = 0 ______(1)
Since (1) passes through (4, 1)
16 + 1 + 8g + 2f + c = 0
⇒ 8g + 2f + c = -17 ______(2)
Since (1) passes through (6, 5)
36 + 25 + 12g + 10f + c = 0
⇒ 12 g + 10f + c = -61 _______(3)
(1) – (2) ⇒ -4g – 8f = 16
⇒ -g – 2f = 4 ______(4)
Since centre is on the line 4x + y = 16, we have;
⇒ -4g – f = 16 ______(5)
Solving (4) and (5) We get; g = -3; f = -4
(2) ⇒ 8(-3) + 2(-4) + c = -17
⇒ -24 – 8 + c = -17 ⇒ c = 15
Then the equation of the circle is
x² + y² – 6x – 8y + 15 = 0.

Question 2.
Find the equation of the circle with radius 5 whose centre lies on x-axis and passes through the point (2, 3).
Answer:
Let the equation of the circle be
(x – h)² + (y – k)² = r²
centre lies on x axis so let the centre be (h, 0),
then (x – h)² + y² = 25
Since circle pass through (2, 3) we have;
(2 – h)² + 3² = 25
⇒ (2 – h)² = 16 ⇒ 2 – h = ±4
⇒ h = 6, -2
When h = 6 ; equation of circle is
(x – 6)² + (y – 0)² = 25
⇒ x² + 36 – 12x + y² = 25
⇒ x² + y² – 12x + 11 = 0
When h = -2; equation of circle is
(x + 2)² + (y – 0)² = 25
⇒ x² + 4 + 4x + y² = 25
⇒ x² + y² + 4x – 21 = 0.

Question 3.
Centre at (0, 0), major axis on the y-axis and passes through the points (3, 2) and (1, 6).
Answer:
Major axis lie on the y-axis so the standard equation of the ellipse is of the form

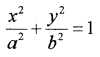
Since the ellipse passes through (3, 2)

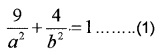
Since the ellipse passes through (1, 6)

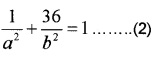
Solving (1) and (2), we have Since the ellipse passes through (3, 2)
a² = 40; b² = 10
Thus the equation of the ellipse is

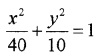
Plus One Maths Conic Sections Six Mark Questions and Answers

Question 1.
Consider the point A (0, 0), B (4, 2) and C (8, 0)

1. Find the mid-point of AB. (1)
2. Find the equation of the perpendicular bisector of AB. (2)
3. Find the equation of the circum circle (Circle passing through the point A, B, and C) of triangle ABC. (3)

Answer:
1. Mid-point of AB is (2, 1).

2. Slope of line through AB
\(=\frac{2-0}{4-0}=\frac{1}{2}\)
Slope of perpendicular line is – 2
Equation of the perpendicular line to AB is
y – 1 = -2(x – 2) ⇒ 2x + y = 5.

3. The meeting point of perpendicular bisector of AB and AC will be the centre of the circum circle.
The line perpendicular to AC is x = 4
Solving and x = 4
We get y = 5 – 8 = -3 and x = 4
Hence centre is (4, -3) and radius is

Equation of the circle is
(x – 4)² + (y + 3)² = 5.

Plus One Maths Conic Sections Practice Problems Questions and Answers

Question 1.
Find the equation of the circle In each of the following cases. (2 score each)

1. Centre (0, 2) and radius 2.
2. Centre (-2, 3) and radius 4.
3. Center \(\left(\frac{1}{2}, \frac{1}{4}\right)\) and radius \(\frac{1}{12}\).

Answer:
1. The equation of the circle is
(x – 0)² + (y – 2)² = 2²
⇒ x² + y² – 4y + 4 = 4
⇒ x² + y² – 4y = 0.

2. The equation of the circle is
(x + 2)² + (y – 3)² = 4²
⇒ x² + 4x + 4 + y² – 6y + 9 = 16
⇒ x² + y² + 4x – 6y – 3 = 0.

3. The equation of the circle is

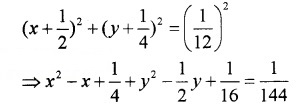
⇒ 144x² + 36 – 144x + 144y² + 9 – 72y = 1
⇒ 144x² + 144y² – 144x – 72y + 44 = 0
⇒ 36x² + 36y² – 36x – 18y + 11 = 0.

Question 2.
Find the centre and radius of the following circles. (2 score each)

1. x² + y² – 4x – 8y – 45 = 0
2. x² + y² – 8x – 10y -22 = 0
3. 2x² + 2y² – x = 0

Answer:
1. Comparing with the general equation we have
g = -2; f = -4; c = -45
Centre – (-g, -f) ⇒ (2, 4)
Radius – \(\sqrt{g^{2}+f^{2}-c}\)

2. Comparing with the general equation we have
g = -4; f = -5; c = -22
Centre – (-g, -f) ⇒ (4, 5)
Radius – \(\sqrt{g^{2}+f^{2}-c}\)

3. Convert the equation into standard form

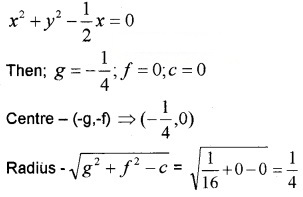
Question 3.
Find the coordinate of the focus, axis of the parabola, the equation of the directrix and the length of the latus rectum. (2 score each)

1. y² = 20x
2. x² = 8
3. 3x² = -15

Answer:
1. Comparing the equation with the general form we get; 4a = 20 ⇒ a = 5
Coordinate of focus are (5, 0)
Axis of the parabola is y = 0
Equation of the directrix is x = -5
Length of latus rectum = 4 × 5 = 20.

2. Comparing the equation with the general form we get; 4a = 8 ⇒ a = 2
Coordinate of focus are (0, 2)
Axis of the parabola is x = 0
Equation of the directrix is y = – 2
Length of latus rectum = 4 × 2 = 8.

3. Convert the equation into general form, we get x² = -5y. Comparing the equation with the general form we get;
4a = 5 ⇒ a = \(\frac{5}{4}\)
Coordinate of focus are (0, \(-\frac{5}{4}\))
Axis of the parabola is x = 0
Equation of the directrix is y = \(\frac{5}{4}\)
Length of latus rectum = \(\frac{4 \times 5}{4}\) = 5.

Question 4.
Find the equation of the parabola satisfying the following conditions; (2 score each)

1. Focus(6, 0); directrix x = – 6
2. Vertex (0, 0); Focus (3, 0)
3. Vertex (0, 0) passing through (2, 3) and axis along x-axis

Answer:
1. Since the focus (6, 0) lies on the x-axis, therefore x-axis is the axis of parabola.
Also the directrix is x = – 6, ie; x = – a And focus (6, 0), ie; (a, 0)
Therefore the equation of the parabola is
y² = 4ax ⇒ y² = 24x.

2. The vertex of the parabola is at (0, 0) and focus is at (3, 0). Then axis of parabola is along x-axis. So the parabola is of the form y² = 4ax . The equation of the parabola is y² = 12x.

3. The vertex of the parabola is at (0, 0) and the axis is along x-axis. So the equation of parabola is of the torn y² = 4ax .
Since the parabola passes through point (2, 3)
Therefore, 3² = 4a × 2 ⇒ a = \(\frac{9}{8}\)
The required equation of the parabola is
y² = 4 × \(\frac{9}{8}\) x ⇒ y² = \(\frac{9}{2}\)x.

Question 5.
Find the Focus, vertex and latus rectum of the parabola y² = 8x.
Answer:
Given; y² = 8x, we have 4a = 8 ⇒ a = 2
Focus = (2, 0); Vertex = (0, 0)
Latus rectum = 4a = 8

Plus One Maths Chapter Wise Questions and Answers