Plus One Maths Chapter Wise Previous Questions Chapter 7 Permutation and Combinations

Kerala Plus One Maths Chapter Wise Previous Questions Chapter 7 Permutation and Combinations

Plus One Maths Permutation and Combinations 3 Marks Important Questions

Question 1.
i) if \({ }^{n} C_{9}={ }^{n} C_{8}\) find ‘n’ and \({ }^{n} C_{17}\) (IMP-2014)
ii) How many chords can be drawn, through 23 points on a circle?
Answer:

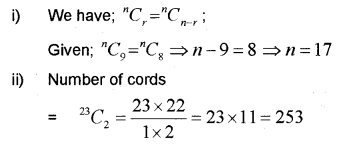
Plus One Maths Permutation and Combinations 4 Marks Important Questions

Question 1.
i) Simplify (MARCH-2011)

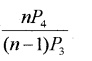
ii) In how many different ways can the letters of the word HEXAGON be permuted?
iii) In how many different ways can a team of 3 boys and 3 girls be selected from 5 boys and 4 girls?
(March (Science) – 2011)
Answer:

Total number of ways = 10 x 4 = 40

Question 2.
i) If \(\frac{1}{8 !}+\frac{1}{9 !}=\frac{x}{10 !}\) (MARCH-2011)
then find x.
ii) How many 4 digit numbers are there with no digit repeated?
iii) If nC₈ = nC₂, then find nC₃ ?
Answer:

Question 3.
Consider all the letters of the word ‘FALIURE’.  (IMP-2011)
i) How many words can be formed using these letters?
ii) How many words can be formed so that the vowels being together?
iii) How many words begin with A and end with E?
(Imp (Commerce) – 2011)
Answer:
i) ‘FALIURE’ word has 7 letters in it, can be arranged in 7! Ways = 7.6.5.4.3.2.1 = 5040
ii)

A,E,I,U are vowels in the word, should be kept together, so should be treated as on block. Hence there are 4 such blocks can be arranged in 4! ways. These 4 vowels can be arranged in 4! Ways.
Hence the total words = 4! x 4! = 24 x 24 = 576
iii)

The only possible arrangement is for 5 blocks; hence total number of ways is 5! = 120.

Question 4.
i) Find the value of n if (IMP-2012)

ii) How many words, with or without meaning,
can be formed using all the letters of the word CHEMISTRY, using each letter exactly once? How many of them start with C and end with Y?
Answer:
i)

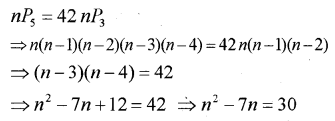
n —10,- 3
n = – 3 is not possible since negative son = 10
ii) Total number of words = 9!
Total number of words starting by C and ending by Y= 7!

Question 5.
i) If 2nC₃ : nC₃ = 12 : 1 find n. (IMP-2012)
ii) What is the total number of ways of choosing 4 cards from a pack of 52 playing cards? In how many of these four cards of the same suit?
Answer:

Question 6.
i) If nC₉ = nC₈, find nC₁₇ 
ii) A committee of 5 person is to be selected from a group of 4 men and 5 women. In how many ways can this be done? How many of these committees would consist of 2 men and 3 women? (IMP-2012)
Answer:

Number of different selection = 6 x 10 = 60

Question 7.
i) If nC₉ = nC₈, find nC₁₇ 
ii) How many three digit number can be formed using the digits 1,2,3,4,5 if repetition is not allowed? (MARCH-2013)
iii) In How many ways can a team of 4 boys and 3 girls be selected from 6 boys and 4 girls?
Answer:

Question 8.
i) If nC₅ = nC₄, find nC₈
ii) How many chords can be drawn through 20 points on a circle? (MARCH-2014)
iii) A bag contains 6 red and 5 blue balls. In how many ways can one choose 3 red and 2 blue balls from this bag?
Answer:

Question 9.
i) Find the number of permutation of the letters of the word ALLAHABAD.
ii) Find r,if \({ }^{5} P_{r}=2 \times{ }^{6} P_{r-1}\) (IMP-2014)
Answer:
i) Total number of letters is 9.
A: 4 times; L: 2 times.

Therefore r = 3.

Plus One Maths Permutation and Combinations 6 Marks Important Questions

Question 1.
i) Find the value of n such that (MARCH-2010)
nP₅ = 42 x nP₃ for n > 4
ii) A committee of 3 persons is to be constituted from a group of 2 men and 3 women.
a) In how many ways can this be done?
b) How many of these committees would consist of 1 man and 2 women? (March (Science) – 2010)
Answer:
i) nP₅ = 42 x nP₂
=> n(n – 1)(n – 2 )(n – 3)(n – 4) = 42 x n(n -1)(n- 2)
=> (n – 3)(n – 4) = 42
=>n² – 7n + 12 = 42
=> n² – 7n – 30 = 0
=> (n -10)(n + 3) = 0
=> n = 10; n = – 3
n can’t be negative, so the acceptable value is n = 10
ii) a) 3 person can be selected from 5 in 5C₃ = 10
(b) 1 man can be selected from 2 in 2C₁ = 2 ways.
2 women can be selected from 3 in 3 C₂ = 3 ways.
Total ways = 2×3 = 6

Question 2.
i) lf \({ }^{n} C_{2}:{ }^{2 n} C_{1}=3: 2\), find n. (MARCH-2010)
ii) a) Find the number of words that can be
formed from the letters of the word MALAYALAM.
b) How many of these arrangements start with Y?
(March (Science) – 2010)
Answer:
i)

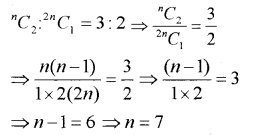
ii) a) MALAYALAM, this word has 9 letters
M- repeated 2 times.
A- repeated 4 times.
L- repeated 2 times.
Number of words formed by these 9 letters
= \(\frac{9 !}{2 ! \times 4 ! \times 2 !}\)
b) If the word starts with Y, then total number of letters that can be arranged become 8. Number of words formed which begin with Y
= \(\frac{8 !}{2 ! \times 4 ! \times 2 !}\)

Question 3.
i) if \(5 \times 4 P_{r}=6 \times 5 P_{r-1}\) find ‘r’, (IMP-2014)
ii) How many 3 digit number can be formed with the digits 0,1,2,3 and 4?
iii) In a Panchayath there are 10 Panchayath members. Ladies contested only in the 50 % reserved constituency. If the post president and vice president are reserved for ladies, in how many ways both the president and vice president can be selected?
(Imp (Science) – 2010)
Answer:
i)

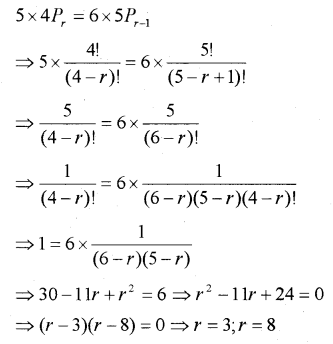
ii)

Total 3 digit numbers = 4x5x5 = 100 (IMP-2010)
iii) The 10 member Panchayath has 5 men and 5 ladies. The president and vice president are to be selected from these ladies in 5C₁₂ = 10 ways.

Question 4.
i) Prove that nC_r = nC_n-r
ii) Twenty eight matches were played in a volley ball tournament. Each team playing one against each of others. How many teams were there? (IMP-2010)
iii) If the letters of the word ‘TUTOR’ be . permuted among themselves and arranged as in a dictionary, then find the position of the word ‘TUTOR’.
Answer:

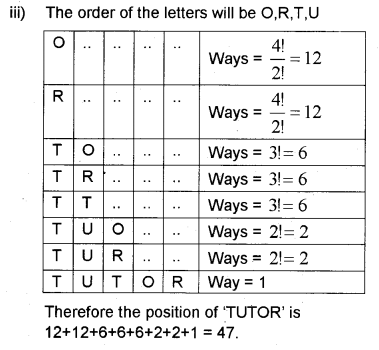
Question 5.
A student is instructed to answer any 8 out of 12 questions. (IMP-2011)
i) How many different ways he can choose the questions?
ii) How many different ways he can choose the questions so that question no.1 will be included?
iii) How many different ways, he can choose the questions so that question no.1 will be included and question no.10 will be excluded?
Answer:
i) 8 out of 12 questions can be selected

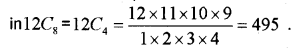
ii) Since question no.1 is included, the possible is selection is from 11 questions and the number of questions to be selected becomes 7.
Hence the total selection

iii) Question no.10 will be excluded so total questions become 11. Question no.1 is included again total questions reduced to 10. Now we have to select 7 questions out of 10, can be done in 10C₇ = 10C₃ = \(\frac{10 \times 9 \times 8}{1 \times 2 \times 3}\) = 120.

Question 6.
Solve for the natural n; (MARCH-2012)
12.(n-1)P10C₃ =5.(n + 1)P10C₃
In how many ways seven althlets can be chosen out of 12?
iii) The English alphabets has 5 vowels and 21 consonants. How many words with two different vowels and two different consonants can be formed without repetition of letters?
Answer:
i)

ii) 7 athletes be chosen out of 12 in 12C₇ =12C₅ ways
iii) Two different vowels can be selected in 5C₂. Two different consonants can be selected in 21C₂.
Therefore total numbers of words

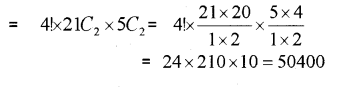
Question 7.
i) Find r if 5P_r = 6P_r-1.
ii) If there are 12 persons in a party and each of them shake hands with all others, what is the total number of handshakes? (MARCH-2012)
iii) In How many ways can a committee of 3men and 2 women be selected out of 7 men and 5 women?
Answer:

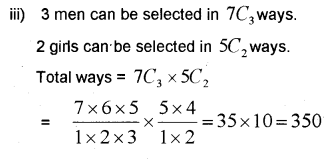
Question 8.
i) Find the value of n such that (MARCH-2013)
3.nP₄ = 5.(n -1 )P₄,n > 4
ii) In how many ways can 5 students be seated on a bench?
iii) Find the number of different 8-letter arrangements that can be made from the letters of the word, ‘DAUGHTER’ so that:
a) All vowels are occur together.
b) All vowels do not occur together.
Answer:

Question 9.
i) Determine n if 2nC₃ = 11.nC₃ 
ii) In how many ways can a cricket team of 11 of players be selected from 15 players? (MARCH-2013)
iii) A bag contains 5 white, 6 red and 4 blue balls. Determine the number of ways in which 2 white, 3red and 2 blue balls can be selected.
Answer:

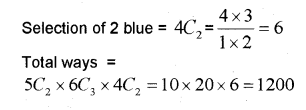
Question 10.
i) The number of 3 digit numbers can be formed from the digits 1,2,3,4,5 assuming that repetition of the digits is not allowed is _______.
ii) If \(\frac{1}{6 !}+\frac{1}{7 !}=\frac{x}{8 !}\), find x. (IMP-2013)
iii) How many words, with or without meaning, can be formed using all the letters of the word ‘FRIDAY’, using each letter exactly once? How many of them have first letter is a vowel?
Answer:

Question 11.
i) nC₇=nC₅,n =
ii) A bag contains 5 blue and 6 white balls. Determine the number of ways in which 3 blue and 4 white balls can be selected. (IMP-2013)
iii) What is number of choosing 3 cards from a pack of 52 playing cards? In how many of these 3 cards of the same colour?
Answer:

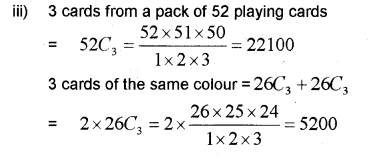
Question 12.
i) if \(\frac{1}{8 !}+\frac{1}{9 !}=\frac{x}{10 !}\) find x? (MARCH-2014)
ii) How many four digit numbers can be formed using the digits 4,5,6,7,8 if repetition of digits is not allowed?
iii) Find the number of arrangements that can be made from the letters of the word ‘MOTHER’ so that all vowels occur together.
Answer:

Question 13.
i) In how many ways can the letters of the word PERMUTATIONS be arranged if; (MARCH-2014)
a) the word starts with P and ends with S?
b) there are always 4 letters between P and S?
ii) In how many ways can 5 girls and 3 boys be seated in a row so that no two boys are together?
iii) How many chords can be drawn through 21 points?
Answer:
i) a) In the word T is repeated twice

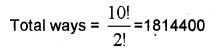
b) P should move from 1 to 7th position and S should move from 6th to 12th position. Hence the arrangements

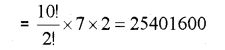
ii) First arrange 5 girls in 5P₅ ways. Arrange 3 boys in 6P₃.
Hence the total arrangements
= 5P₅ x 6P₃ = 14400
iii) Chord is the join of two points. Hence selection 2 points from 21, which can be done in 21C₂ =210

Question 14.
i) What is the minimum number of ways of choosing 4 cards from a pack of 52 playing cards? In how many of these
a) are 4 cards of the same suit? (MARCH-2014)
b) do 4 cards belong to 4 different suits?
ii) Find the number of permutation of the letters of the word, ALLAHABAD.
iii) How many 5-digit telephone numbers can be constructed using the digits 0 to 9 if each number starts with 67 and no digit appears more than once?
Answer:

Question 15.
i) Find ‘n’ if \(9 \times^{(n-1)} P_{3}={ }^{n} P_{4}\) (IMP-2014)
ii) Find the number of words that can be formed from the letters of the word, COMMERCE’.
iii) In how many ways can a group of 12 students be selected from 15 students? How many of these groups would include one particular student?
Answer:

Question 16.
i) \(\frac{0 !}{1 !}\) = _____ (MARCH-2015)
a) 0
b) 1
c) 2
d) 3
ii) Find r, if \(5 \times^{4} P_{r}=6 \times^{5} P_{r-1}\)
iii) Find the number of 8-letter arrangements that can be made from the letters of the word DAUGHTER so that all vowels do not occur together.
Answer:

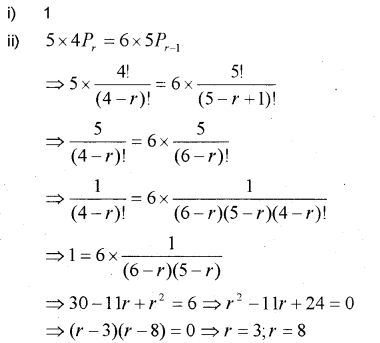
Question 17.
nC_{n – 1} = _____ (MARCH-2015)
(a) n-1
(b) n
(c) 0
(d) 1
If nC₉=nC₈,find nC₂
How many ways can a team of 5 persons be selected out of a group of 4 men and 7 women, if the team has at least one man and one women?
Answer:

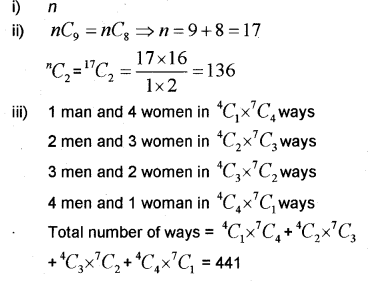
Question 18.

i) \({ }^{7} P_{7}\) = _____ (IMP-2014)
a) 7
b) 7!
c) 1
d) 77
ii) Find the number of words that can be formed from the letters of the word “MALAYALAM”. How many of them start with Y?
iii) \({ }^{2 n} C_{3}=11 \times{ }^{n} C_{3}\) Find ’n’.
Answer:

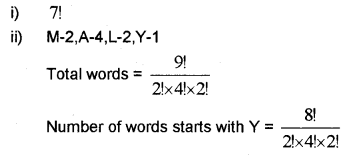
iii)

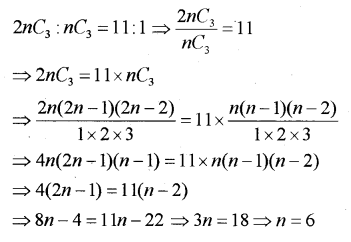
Question 19.
i) \({ }^{29} C_{29}\) = ______ (IMP-2015)
(a) 0
(b) 1
(c) 2
(d) 3
ii) Prove that \({ }^{61} C_{57}-{ }^{60} C_{56}={ }^{60} C_{3}\)
iii) In how many ways can the letters of the word ‘ARRANGE’ be arranged such that two A’s do not occur together?
Answer:

Question 20.
Write the value of \({ }^{7} C_{5}\) (MARCH-2016)
Find the vale of n, if \(3 \times^{n} P_{4}=5 \times^{n-1} P_{4}\)
What is the number of ways of choosing 4 cards from a pack of 52 cards, provided all 4 cards belong to 4 different suits? (March (Science) – 2016)
Answer:

Question 21.
i) \({ }^{29} C_{29}\) = ______ (MARCH-2016)
a) 0
b) 1
c )2
d )3
ii) Find the value of n,
if \(12 \times^{n-1} P_{3}=5 \times^{n+1} P_{3}\)
iii) A group consists of 4 girls and 7 boys. In how many ways can a team of 5 members be selected if the team has at least one boy and one girl?
Answer:

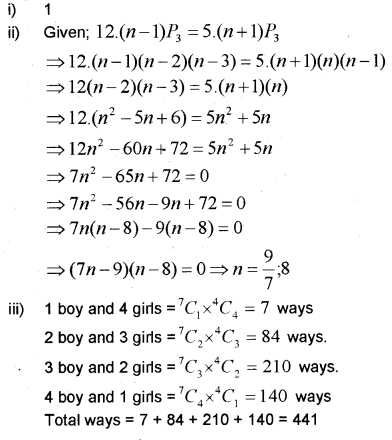
Question 22.
i) How many 4 digit numbers can be formed using the digits 9, 8, 7, 6, 5, 4, if no digits are repeated? (MAY-2017)
(a) 630
(b) 603
(c) 306
(d) 360
ii) In how many ways a committee of 3 persons can be formed from a group of 2 men and 3 women?
iii) Find the value of n,
if \({ }^{2 n} C_{3}=11 \times{ }^{n} C_{3}\)
Answer:

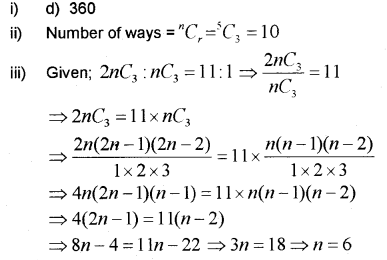
Question 23.
i) \({ }^{569} \mathrm{C}_{569}\) = ______. (MAY-2017)
ii) \({ }^{2 n} C_{3}:{ }^{n} C_{3}=12: 1\) Find n.
iii) If the letters of the word EQUATION are arranged, find the number of arrangements in which no two consonants occur together?
Answer:
i) 1

Question 24.
i) if \(\frac{1}{6 !}+\frac{1}{7 !}=\frac{x}{8 !}\) , then x is ______.
(a) 32
(b) 16
(c) 64
(d) 8
ii) Given 5 flags of different colour, how many different signals can be generated if each other.
iii) Find r, if \({ }^{5} P_{r}=2 \times{ }^{6} P_{r-1}\)
Answer:
i) c) 64
ii) Number of ways = 5 x 4 = 20

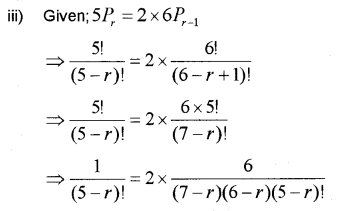
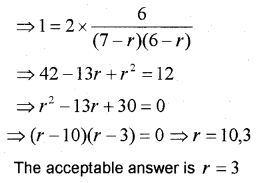
Question 25.
i) lf nC₉=nC₈, then n = ______.
a) 9
b) 8
c) 17
d) 1
ii) How many chords can be drawn through 12 point on a circle?
iii) What is the number of way of choosing 4 cards from a pack 52 playing cards? In how many of these:
a) Four cards are of the same suit.
b) Cards are of the same colour.
Answer:

Plus One Maths Chapter Wise Previous Questions and Answer