Kerala Plus One Maths Chapter Wise Previous Questions Chapter 1 Sets
Plus One Maths Sets 3 Marks Important Questions
Question 1.
Consider the sets A and B given by (MARCH-2010)
A = {x\ x is a natural number, 2 ≤ x ≤ 6 }
B = {x: x is a prime number x ≤ 7 }
C = {x: x² – 5x + 6 = 0 }
i) Write A, B and C in the roster form.
ii) Verify that(A∪B)∪C = A∪(B∪C)
Answer:
i) A = {2,3,4,5,6}; B = {2,3, 5,7};
x² – 5x + 6 = 0
=> (x – 2)(x – 3) = 0
x = 2,3
C = {2,3}
ii) A∪B = {2,3,4,5,6,7};
(A∪B)∪C = {2,3,4,5,6,7}
B∪C = {2,3,5,7};
A∪(B∪C )= {2,3,4,5,6,7}
Hence;
(A∪B)∪C = A∪(B∪C)
Question 2.
Consider the sets A and B given by (MARCH-2011)
A = {x: x is a prime number <10}
B = {y. x is a natural number which divides 12}
i) Write A and B in the roster form.
ii) Find A∪BandB-A.
iii) Verify that(A∪B) – A = B – A.
Answer:
i) A = (2,3,5,7};B = {1,2,3,4,6,12}
ii) A∪B = {1,2,3,4,5,6,7,12};
B-A = {1,4,6,12}
iii) (A∪B)-A = {1,4,6,12} = B – A
Plus One Maths Sets 4 Marks Important Questions
Question 1.
If A = {1},
B = {{1},2}
C = {{1}, 3} and ∪ = {{1}, {2}, {3},1,2,3}, then find (IMP-2010)
i) A∩B
ii) B∩C
iii) n{{A∩B)’∪(B∩C)’)
Answer:
i) A∩B = 𝟇
ii) B∩C={{1}}
iii) (A∩B)’ = ∪ ;
(B∩C)’ = {{2},{3},1,2,3}
(A∩B)’∪(B∩C)’ = U∪{ {2}, {3} ,1,2,3} =U
n((A∩B)'{B∩C)’)= 6
Question 2.
Given U = {1,2,3,4,5,6,7,8,9,10},A= {1,2,3,4,5} and B = {3,4,5,6} (IMP-2011)
i) Write A∪B
ii) Verify whether(A∪B) ‘ = A’∩B’
iii) Verify whether
n(A∪B)=n(A-B)+n(A∩B)+n(B – A)
Answer:
i) A∪B = {1,2,3,4,5,6}
ii) A’ = {6,7,8,9,10} ,B’-= {1,2,7,8,9,10}
A’∩B’ = {7,8,9,10}
(A∪ B)’ = {7,8,9,10}
Hence (A∪B)’ = A’∩B’
iii) (A – B)={1,2};B – A = {6}; A∩B = {3,4,5}
n(A∪B) = 6,n(A – B) = 2,
n{B-A) = 1,n(A∩B) = 3
n(A -B) + n(A ∩ B) + n(B -A)
= 2 + 3 +1 = 6
= n(A ∪ B)
Hence verified.
Question 3.
Let A = {x:x is an integer \(\frac{1}{2}<x<\frac{7}{2}\) } and B = {2,3,4} (MARCH-2012)
i) Write A in the roster form.
ii) Find the power set of (A∪ B).
iii) Verify that(A-B)∪(A∩B) = A
Answer:
i) A = {1,2,3}
ii) A ∪ B= {1,2,3,4}
P(A) = {𝟇, {1} ,{2}, {3}, {4}, {1,2}, {1,3}, {1,4},{2,3},{2,4},{3,4},{1,2,3},{1,2,4},{1,3,4}, {2,3,4}, {1,2,3,4}}
iii) (A – B)∪(A ∩ B)
= {1} ∪ {2,3} = {1,2,3} = A
Question 4.
i) How many elements has P(A) if A = {1,2,3}? (IMP-2012)
ii) U = {1,2,3,4,5,6,7}; A = {1,4,6,7}; B = {1,2,3}. Find
A’,B’,A’∩B’,A∪B and
hence show that A’ ∩ B’ = (A ∪ B)’.
iii) If A and B are two sets such that A⊂B, then what is A ∩ B ?
Answer:
i) n(P(A)) = 2³ = 8
ii) A’ = {2,3,5},B’= {4,5,6,7}
A’ ∩B’ = {5}
A∪B = {1,2,3,4,6,7} =>(A∪B)’={5}
Hence A’∩B’ = (A∪ B)’
iii) A∩B = A
Question 5.
i) Let A = {1,2,3,5,6} and B = {1,3,4,6,7} (MARCH-2013)
a) Find A ∪ B? and A ∩B?
b) Find A -(A ∩B)
ii) If X and Y are two sets such that n(X) = 17, n{Y) = 23 and n(X∪Y)=38, find n(X∩Y).
Answer:
i) a) (A∪B) = {1,2,3,4,5 6,7} ,A∩B = {1,3,6}
b) A – (A∩B) = A – {1,3,6} = {2,5}
ii) We have; n(X∪Y)=n(X) + n(Y) – n(X∩Y)
38 = 17 + 23 – n(X∩Y)
n(X∩Y)= 40 – 38 = 2
Question 6.
Let ∪ = {1,2,3,4,5,6,7,8,9}, A = {1,2,4,7} and B = {1,3,5,7} (MARCH-2013)
i) Find A∪B.
ii) Find A’, B’ and hence show that
(A∪B)’ = A’∩B’
iii) The power set P(A) has …………. elements.
Answer:
i) A∪B={l,2,3,4,5,7}
ii) A’ = {3,5,6,8,9} ,B’ = {2,4,6,8,9}
(A∪B)’ = {6,8,9} = A’ ∩B’
iii) 2⁴= 16
Question 7.
i) If two sets A and B are disjoint, which none among the following is true? (IMP-2014)
a) A∪B = A
b)A∪B = B
c) A∩B = A
d )A∩B = 𝟇
ii) Find the set of the equation x² + x – 2 = 0 in roster form.
iii) In a group of students, 100 students know Hindi, 50 know English and 33 know both. Each of the students knows either Hindi or English. How many students are there in the group?
Answer:
i) d)A∩B = 𝟇
ii) x² + x – 2 = 0
=> (x – 1)(x + 2) = 0 =>
x = 1;-2
Solution set is {1,-2}
iii) Let H-Hindi; E- English
n(H) = 100;
n(E) = 50;
n(H ∩E) = 33
n(H ∪ E) = n(H) + n(E) – n(H ∩ E)
= 100 + 50-33 = 117
Question 8.
Let A = {x: x ∈ W ,x<5} and B = (x : x is a prime number less than 5} and U = {x: x is an integer O ≤ x ≤ 6} (MARCH-2015)
i) Write A,B in roster form.
ii) Find (A-B)∪(B-A)
iii) Verify (A ∪ B)’ = A’ ∩ B’
Answer:
i) A= {0,1,2,3,4}; B = {2,3}
ii) A – B = {0,1,4}; B – A ={ }
iii) U= {0,1,2,3,4,5,6}
A’ = {5,6}, B’ = {0,1,4,5,6}
(A∪B)’ = {5,6}
A’ ∩ B’ = {5,6}
Question 9.
If U = {1,2,3,4,5,6,7,8}, A = {2,4,6,8} and B = {2,4,8} (MAY-2016)
then:
i) Write A’, B’.
ii) For the above sets A and B prove that (A∪B)’ = A’∩B’
iii) Check whether (A∩B)’ = A’∪B’
Answer:
i) A’ = {1,3,5,7};B’ = {1,3,5,6,7}
ii) A ∪ B = {2,4,6,8}, (A ∪ B)’ = {1,3,5,7}
A’∩B’ = {l,3,5,7} => (A∪B)’ = A’∩B’
iii) A ∩ B = {2,4,8}; (A ∩ B)’ = {1,3,5,6,7}
A’∪B’ = {1,3,5,6,7} => (A∩B)’ = A’∪B’
Plus One Maths Sets 6 Marks Important Questions
Question 1.
i) What is A∪A’? (IMP-2012)
ii) If A and B are two sets such that n(A∪B) = 17 and n(A∩B) = 5,
find n(A) + n(B)
iii) In a group of 100 peoples, 40 people like cinema, 10 like both drama and cinema. How many like drama? How many like drama only not cinema?
Answer:
i) A∪A’ = ∪
ii) We have; A(A∪B)=n(A) + n(B) – n(A∩B)
=> 17 = n(A) + n(B) – 5
=> n(A) + n(B) = 17 + 5 = 22
iii) Let D – is the set of Drama, C is the set of Cinema.
Given;
n(D∪C) = 100, n{C) = 40, n(D∩C) = 10,
n(D ∪ C) = n(D) + n(C) – n(D ∩ C)
=>100 = n(D) +40 – 10
=> n(D) = 100-40 +10 = 70
n(Drama not Cinema) = n(D ∩ C’)
= n(D) – n(D∩C) = 70-10 = 60
Question 2.
i) If A and B are two sets such that A ⊂ B, (IMP-2013)
a) A ∪B is
b) Draw the Venn diagram of B – A
ii) In a committee, 60 people speak English,30 speak Hindi and 15 speak both English and Hindi. How many speak atleast one of these two languages?
Answer:
i) a) B
b)
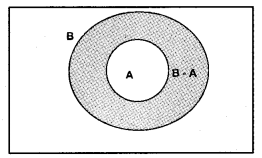
ii) Let the events be E – English and H – Hindi
n(E) = 60; n(H) = 30; n(E∩H) = 15
People speak atleast one of these two languages = n(E∪H)
= n(E) + n(H)-n(E∩H)
= 60 + 30 – 15 = 75
Question 3.
Consider the set A = {2,3,5,7} and B = {1,2,3,4,6,12} (MARCH-2014)
i) Find A∩B.
ii) Find A – B,B – A and hence show that (A∩B)∪(A – B)∪(B – A)=A∪B
iii) Write the power set of A ∩ B
Answer:
i) A ∩ B = {2,3}
ii) A – B = {5,7} ,B-A = {1,4,6,12}
(A∪ B) = {1,2,3,4,5,6,712}
(A ∩B) ∪(A – B) ∪ (B – A) = {1,2,3,4,5,6,7,12}
iii) P(A∩B) = {𝟇,{2},{3},{2,3}}
Question 4.
i) If A = {1,2,3,4} and B = {3,4,5,6} then (MARCH-2014)
A – B= ………
(ii) In a group of 70 people, 37 like coffee, 52 like tea and each person likes atleast one of the two drinks. How many people like both coffee and tea?
iii) Let U = {1,2,3,4,5,6}, A= {2,3} and B = {3,4,5}. Find A’,B’and hence show that (A ∪ B)’ = A’ ∩ B’
Answer:
i) A – B = {1,2}
ii) n(C∪T) = 70,n(C) = 37,n(t) = 52 ,n(C∪T) = n(C) + n(T) – n(C∩T)
=> 70 = 37 + 52 – n(C ∩ T)
=> n(C ∩ T) = 89 – 70 = 19
iii) A= {1,4,5,6},B’ = {1,2,6}
A’∩B’ = {1,6}
{A∪B)’ = ({2,3,4,5})’ = {1,6}
Hence; (A∪ B)’= A’ ∩ B’
Question 5.
Let A= {1,2,3,4,5}, B = {1,2,6} and C = {1,6,7,8} (IMP-2014)
i) Find A∪B and B∩C
ii) Show that
A∪(B∩C) = (A ∪ B)∩(A ∪ C)
iii) Find A – (B∩C) and (A ∪ B) – (B∩C)
Answer:
i) A∪B = {1,2,3,4,5,6}
(B∩C) = {1,6}
ii) A∪ (B∩C) = {1,2,3,4,5} ∪ {1,6}
= {1,2,3,4,5,6}
A∪C = {1,2,3,4,5,6,7,8}
(A ∪ B) ∩ (A ∪ C) = {1,2,3,4,5,6}
Hence A∪(B∩C) = (A∪B)∩(A∪C)
iii) A- (B∩C) = {1,2,3,4,5} – {1,6} = {2,3,4,5}
(A∪B) – (B∩C) = {2,3,4,5}
Question 6.
i) A: {x : x is a prime number x ≤ 6} (IMP-2015)
a) Represent A in Roster form.
b) Write the Power set of A.
ii) Out of 25 members in an office 17 like to take tea, 16 like to take coffee. Assume that each takes at least one of the two drinks. How many like (a) Both coffee and tea? (b) Only tea and not coffee?
Answer:
i) A ={2,3,5}
ii) P(A) = {𝟇,{2},{3},{5},{2,3},{2,5},{3,5},{2,3,5}}
iii) Let the sets be defined as follows;
T- Tea; C – Coffee.
n(T) = 17; n(C) = 16; n(T ∪ C) = 25
n(T ∪ C) = n(T) + n(C) – n(T ∩ C)
Coffee and Tea = n(T∩C) = 17 + 16 – 25 = 8
Only tea and not coffee =
n(T ∩C’) = n(T) – n(T∩C) = 17 – 8 = 9
Question 7.
i) If A is a subset of the set B, then (MARCH-2016)
A∩B = _____
ii) Represent the above set A∩B by Venn diagram.
iii) In a school, there are 20 teachers who teach Mathematics or Physics. Of These, 12 teach Mathematics, 12 teach Physics. How many teach both the subject?
Answer:
i) A
ii)
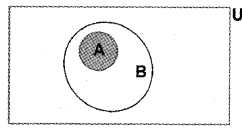
iii) Let the sets be defined as follows;
M- Mathematics; P – Physics.
n(M) = 12
n(P) = 12;
n(M∩P) = 20
n(M ∪ P) = n(M) + n(P) – n(M ∩ P)
n(M ∪ P) = 12 +12- 20 = 4
Question 8.
i) If U is the universal set and A is any set U∩A (MARCH-2017)
(a) U
(b) A
(c)𝟇
(d) A’
ii) Consider the sets
U = {a,b,c,d,e,f,g}, A = {b,c,d,e}, B = {a,c,g). Find A’and B’ the verify (A∪B)’ = A’∩B’
iii) In a group of 400 people, 250 speaks Hindi, 200 can speak Malayalam. How many people can speak both Malayalam and Hindi?
Answer:
i) b) A
ii) A∪B = {a,b,c,d,e,g}
A’ = {a,f,g} ;
B’ = {b,d,e,f};
(A∪B)’ = {f}; A’∩B’ = {f}
iii) n(A∩B) = 400,n(A) = 250
n(B) = 200
n(A ∩ B) = n(A) + n(B) – n(A ∪ B)
= 250 + 200 – 400
= 50