Plus One Computer Science Notes Chapter 2 Data Representation and Boolean Algebra

Kerala Plus One Computer Science Notes Chapter 2 Data Representation and Boolean Algebra

Number System:
It is a systematic way to represent numbers in different ways. Each number system has its own Base, that is a number and that number of symbols or digits used.

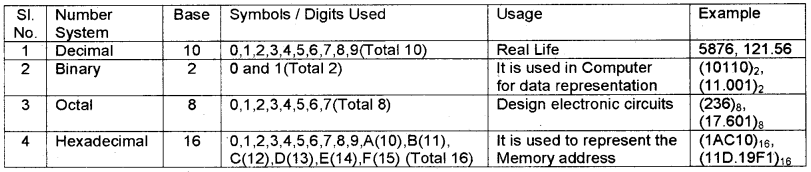
1. Most Significant Digit (MSD): The digit with most weight is called MSD. MSD is also called Left Most Digit(LMD)
2. Least Significant Digit (LSD): The digit with least weight is called LSD. LSD is also called Right Most Digit(RMD)
   • eg: 106 : Here MSD : 1 and LSD : 6
   • 345.78: Here MSD : 3 and LSD : 8
3. A Binary Digit is also called a bit.
4. The weight of each digit of a number can be represented by the power of its base.

Number conversions:
In general, to convert a decimal number into another number system(binary or octal or hexadecimal) do the following. Divide the number successively by the base of the number system do you want to convert and write down the remainders from bottom to top.

To convert a decimal fraction into another number system .multiply the number by the base of the number system do you want to convert then integer part and fractional part are separated again multiply the fractional part by the base and do the steps repeatedly until the fractional part becomes zero. Finally write down the integer part from top to bottom.

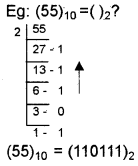
Decimal to Binary:
Divide the number by the base 2 successively and write down the remainders from bottom to top.

Decimal fraction to binary:
multiply the number by the base 2 then integer part and fractional part are separated again multiply the fractional part by the base 2 and do the steps repeatedly until the fractional part becomes zero. Finally write down the integer part from top to bottom.

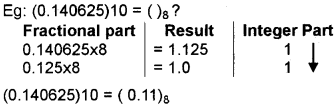
Decimal to Octal:
Divide the number by the base 8 successively and write down the remainders from bottom to top.

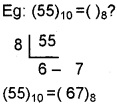
Decimal fraction to octal:
multiply the number by the base 8 then integer part and fractional part are separated again multiply the fractional part by the base 8 and do the steps repeatedly until the fractional part becomes zero. Finally write down the integer part from top to bottom.
eg: (55)₁₀ = ()₈

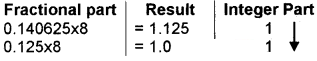
(0.140625)₁₀ = (0.11)₈

Decimal to Hexadecimal:
Divide the number by the base 16 successively and write down the remainders from bottom to top.

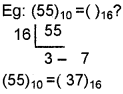
Decimal fraction to hexadecimal:
multiply the number by the base 16 then integer part and fractional part are separated again multiply the fractional part by the base 16 and do the steps repeatedly until the fractional part becomes zero. Finally write down the integer part from top to bottom.

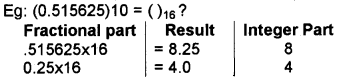
Converting a number from any number system into decimal: For this multiply each digit by its corresponding weight and sum it up.

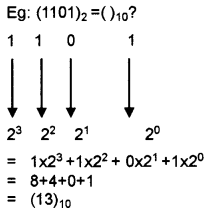
Binary to decimal conversion:
For this multiply each bit by its corresponding weight and sum it up. The weights are power of 2.

Converting binary fraction to decimal

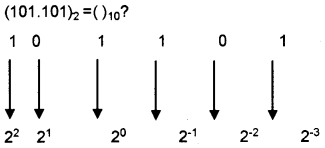
101.101 = 1 × 2² + 0 × 2¹ + 1 × 2⁰ + 1 × 2^-1 + 0 × 2^-2 + 1 × 2^-3
= 4 + 0 + 1 + 1/2 + 0 + 1/8
= 5 + 0.5 + 0.125
(101.101)₂ = (5.625)₁₀

Octal to decimal conversion:
For this multiply each bit by its corresponding weight and sum it up. The weights are power of 8.
Eg: (1007)₈ =()₁₀?

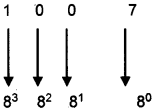
1 × 8³ + 0 × 8² + 0 × 8¹ + 7 × 8⁰
= 512 + 0 + 0 + 7
=(519)₁₀
Converting octal fraction to decimal (600.005)₈ =()₁₀?

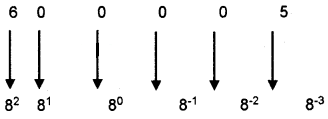
= 6 × 8² + 0 × 8¹ + 0 × 8⁰ + 0 × 8^-1 + 0 × 8^-2 + 5 × 8^-3
= 384 + 0 + 0 + 0 + 0 + 0.009765625
= (384.009765625)₁₀

Hexadecimal to decimal conversion:
For this multiply each bit by its corresponding weight and sum it up. The weights are power of 16.
Eg: (100)₁₆ = ()₁₀?

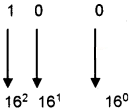
= 1 × 16² + 0 × 16¹ + 0 × 16⁰
= 256 + 0 + 0
= (256)₁₀
Converting Hexadecimal fraction to decimal (60A.4)₈ =()₁₀?

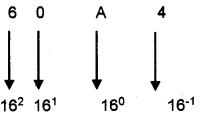
= 6 x 16² + 0 x 16¹ + 10 x 16⁰ + 4 x 16^-1
= 1536 + 0 + 0 + .25
= (1536.25)₁₀

Octal to binary conversion:
Convert each octal digit into its 3 bit binary equivalent. Consider the following table

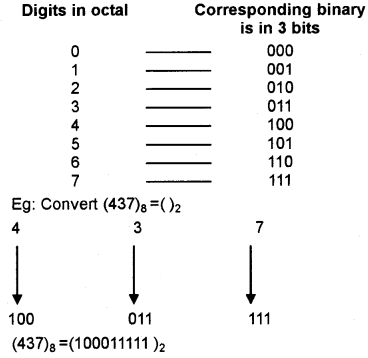
Hexadecimal to binary conversion:
Convert each Hexadecimal digit into its 4 bit binary equivalent. Consider the following table

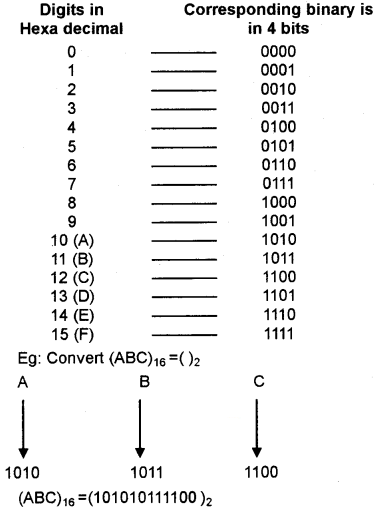
1010 1011 1100 (ABC)₁₆=(101010111100)₂

Binary to octal conversion
Divide the binary number into groups of 3 bits starting from the right to left(But in the fractional part start dividing from left to right). Insert necessary zeros in the left side(or right side in the case of fractional part)if needed and write down the corresponding octal equivalent.
eg: (10100110)₂= ()₈?
Insert one zero in the left side to form 3 bits group

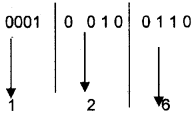
(10100110)₂= (246)₈

Binary to Hexadecimal conversion:
Divide the binary number into groups of 4 bits starting from the right to left(But in the fractional part start dividing from left to right). Insert necessary zeros in the left side(or right side in the case of fractional part)if needed and write down the corresponding Hexadecimal equivalent.
eg: (100100110)₂ = ()₁₆?
Insert 3 zeros in the left side to form 4 bits group

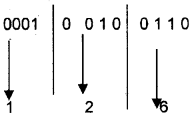
(100100110)₂ = (126)₁₆

Octal to Hexadecimal conversion:
First convert octal number into binary(see 1.6.7), then convert this binary into hexadecimal(also see 1.6.10)
eg: Convert (67)₈ = ( )₁₆
Step I: First convert this number into binary equivalent for this do the following:

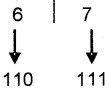
Step II: Next convert this number into hexadecimal equivalent for this do the following.

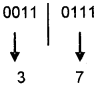
So the answer is (67)₈ = ( 37)₁₆

Hexadecimal to octal conversion:
First convert Hexadecimal to binary(see 1.6.8), then covert this binary into octal(also see 1.6.9)
eg: Convert (A1)₁₆ = ( )₈?
Step I: First convert this number into binary equivalent. For this do the following

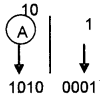
Step II. Next convert this number into octal equivalent. For this do the following.
So the answer is (A1)₁₆ = (241)₈

Data representation:
The data stored in the computer memory is in the form of binary.

Representation of integers
There are three ways to represent integers in computer. They are as follows:

1. Sign and Magnitude Representation (SMR)
2. 1’s Complement Representation
3. 2’s Complement Representation

1. SMR:
Normally a number has two parts sign and magnitude, eg: Consider a number+5. Here + is the sign and 5 is the magnitude. In SMR the most significant Bit (MSB) is used to represent the sign. If MSB is 0 sign is +ve and MSB is 1 sign is -ve. eg: If a computer has word size is 1 byte then

Here MSB is used for sign then the remaining 7 bits are used to represent magnitude. So we can , represent 2⁷ = 128 numbers. But there are negative and positive numbers. So 128 + 128 = 256 number. The numbers are 0 to +127 and 0 to -127. Here zero is repeated. So we can represent 256 – 1 = 255 numbers.

2. 1’s Complement Representation:
To get the 1’s complement of a binary number, just replace every 0 with 1 and every 1 with 0. Negative numbers are represented using 1’s complement but +ve number has no 1 ’s complement,
eg:
(i) To find the 1’s complement of -21
+21 = 00010101
To get the 1’s complement change all 0 to 1 and.all 1 to 0.
-21 = 11101010
1’s complement of-21 is 11101010

(ii) Find the 1’s complement of +21. Positive numbers are represented by using SMR.
+21 = 00010101 (No need to take the 1’s complement)

3. 2’s Complement Representation:
To get the 2’s complement of a binary number, just add 1 to its 1’s complement +ve number has no 2’s complement.
eg: To find the 2’s complement of -21
+21 = 00010101
First take the 1’s complement for this change all 1 to 0 and all 0 to 1

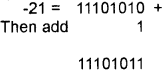
2’s complement of -21 is 1110 1011

Representation of floating point numbers:
A real number consists of an integer part and fractional part and represent by using Exponent and Mantissa method. This method is also used to represent too big numbers as well as too small numbers.
Eg: .0000000000000000000000001 can be represented easily as 1 × 10^-25. Here T is the Mantissa and -25 is the exponent.

A computer with 32 bit word length is used 24 bits for mantissa and the remaining 8 bits used to store exponent.

Representation of characters:
1. ASCII(American Standard Code for Information Interchange):
It is 7 bits code used to represent alphanumeric and some special characters in computer memory. It is introduced by U.S. government. Each character in the keyboard has a unique number.

Eg: ASCII code of ‘a’ is 97, when you press ‘a’ in the keyboard , a signal equivalent to 1100001 (Binary equivalent of 97 is 1100001) is passed to the computer memory. 2⁷ = 128, hence we can represent only 128 characters by using ASCII. It is not enough to represent all the characters of a standard keyboard.

2. EBCDIC(Extended Binary Coded Decimal Interchange Code):
It is an 8 bit code introduced by IBM(lnternational Business Machine). 2⁸ = 256 characters can be represented by using this.

3. ISCII(lndian Standard Code for Information Interchange):
It uses 8 bits to represent data and introduced by standardization committee and adopted by Bureau of Indian Standards(BIS).

4. Unicode:
The limitations to store more characters is solved by the introduction of Unicode. It uses 16 bits so 2¹⁶ = 65536 characters (i.e, world’s all written language characters) can store by using this.

Binary arithmetic:
Binary addition:
The rules for adding two bits

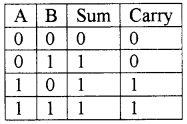
eg: Find the sum of binary numbers 110011 and 100001.

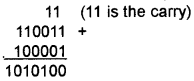
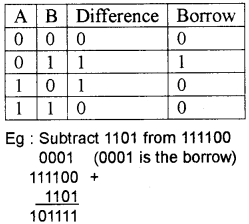
Binary subtraction:
The rules for subtracting a binary digit from another digit.

Subtraction using 1’s complement:
The steps are given below:

Step 1: Add 0s to the left of the subtrahend, to make two numbers with same number of bits.
Step 2: Find 1’s complement of subtrahend.
Step 3: Add the complement with minuend.
Step 4: If there is a carry, ignore the carry, the result is positive then add the carry 1 to the result.
eg: Subtract 1101 from 111100 using 1’s complement method.
Step 1: Insert two Os to the left of 1101. Hence the subtrahend is 001101.
Step 2: 1’s complement of 001101 is 110010
Step 3: Add this to the minuend.

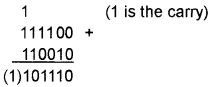
Step 4: Ignore the carry the result is positive and add add the carry 1 to 101110

Hence the result is 101111.

Subtraction using 2’s complement:
The steps are given below :
Step 1: Add 0s to the left of the subtrahend, to make two numbers with same number of bits.
Step 2: Find 2’s complement of subtrahend.
Step 3: Add the complement with minuend.
Step 4: If there is a carry, ignore the carry, the result is positive.
eg: Subtract 1101 from 111100 using 2’s complement method.
Step 1: Insert two 0s to the left of 1101. Hence the subtrahend is 001101.
Step 2: Find the 2’s complement of 001101.
1’s complement is 110010.
2’s complement is 110010 + 1 = 110011
Step 3: Add this to the minuend.

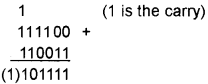
Step 4: Ignore the carry the result is positive. Hence the result is 101111.

Introduction to Boolean algebra:
The name Boolean Algebra is given to honour the British mathematician George Boole. Boolean algebra deals with two states true or false otherwise Yes or No and numerically either 0 or 1.

Binary valued quantities:
A logical decision which gives YES or No values is a binary decision, A statement which gives YES or NO values(TRUE or FALSE) is a logical statement or truth function. A variable which can assign TRUE or FALSE (1 or 0) values is a logical variable

Boolean operators and logic gates:
Logical Operators are AND, OR and NOT. A logical gate is a physical device (electronic circuit)that can perform logical operations on one or more logical inputs and produce a single logical output. A table represents the set f all possible values and the corresponding results in a statement is called truth table.
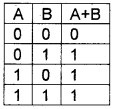
1. The OR operator and OR gate:
The OR operator gives a 1 either one of the operands is 1. If both operands are 0, it produces 0. The truth table of X OR Y is

The logical OR gate is given below.

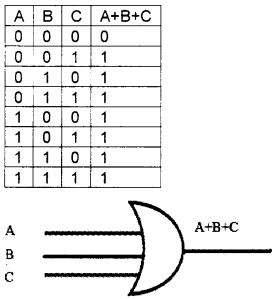
The truth table and the gate for the Boolean expression Y = A + B + C

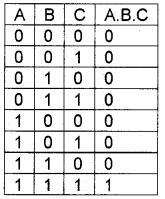
2. The AND operator and AND gate:
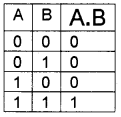
The AND operator gives a 1 if and only if both operands are 1. If either one of the operands is 0, it produces 0 The truth table of X AND Y is

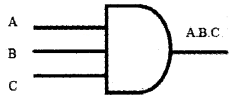
The logical AND gate is given below.

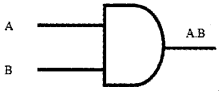
The truth table and the gate for the Boolean expression Y = A . B . C

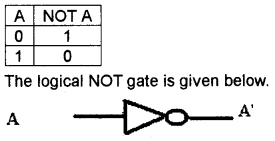
3. The NOT operator and NOT gate:
It produces the vice versa. NOT gate is also called inverter. It is a unary operator that means it has only one input and one output. The truth table of NOT X is

Basic postulates of Boolean algebra:
Boolean algebra consists of some fundamental laws. These laws are called postulates.
Postulate 1: Principles of 0 and 1
If A ≠ 0 , then A = 1 and A 1, then A = 0

Principle of Duality:
When changing the OR(+) to AND(.), AND (.) to OR(+), 0 to 1 and 1 to 0 in a Boolean expression we will get another Boolean relation which is the dual of the first, this is the principle of duality.

Basic theorems of Boolean algebra:
There are some standard and accepted rules in every theory, these rules are known as axioms of the theory.

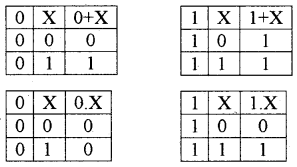
Identity law:
If X is a Boolean variable, the law states that

1. 0 + X = X
2. 1 + X = 1 (these are additive identity law)
3. 0 . X = 0
4. 1 . X = X (these are multiplicative identity law)

Following are the truth tables

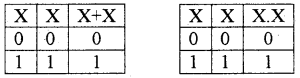
Idempotent law:
This law states that

1. X + X = X
2. X . X = X

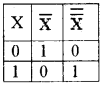
Involution law:
This states that
\(\overline{\overline{\mathrm{X}}}=\mathrm{x}\)
The compliment of compliment of a number is the number itself.

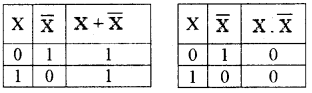
Complimentary law:
This law states that

1. \(x+\bar{x}=1\)
2. \(x \cdot \bar{x}=0\)

The truth table is given below

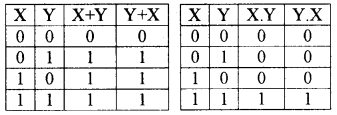
Commutative law:
This law allows to change the position of variable in OR and AND

1. X + Y = Y + X
2. X . Y = Y . X

The truth table is given below

Associative law:
It allows grouping of variables differently

1. X + (Y + Z) = (X + Y) + Z
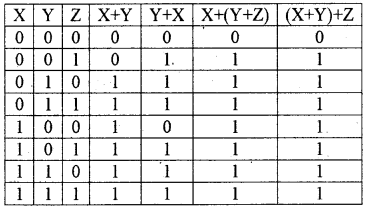
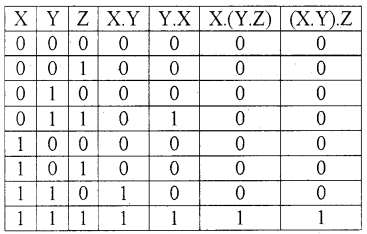
2. X . (Y . Z) = (X . Y) . Z

The truth table is given below

Distributive law:
This law allows expansion of multiplication over addition and also allows addition operation over multiplication.

1. X . (Y + Z) = X . Y + X . Z
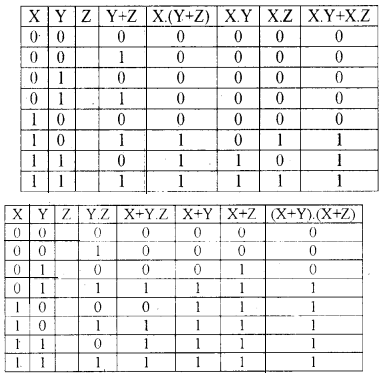
2. X + Y . Z = (X + Y) . (X + Z)

The truth table is given below

Absorption law:
It is a kind of distributive law in which two variables are used and result will be one of them

1. X + (X . Y) = X
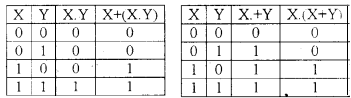
2. X . (X + Y) = X

The truth table is given below

De Morgan’s theorem:
Demorgan’s first theorem states that
\(\overline{\mathrm{X}+\mathrm{Y}}=\overline{\mathrm{X}} \cdot \overline{\mathrm{Y}}\)
ie. the compliment of sum of two variables equals product of their compliments.

The second theorem states that
\(\overline{\mathrm{X} . {\mathrm{Y}}}=\overline{\mathrm{X}}+\overline{\mathrm{Y}}\)
ie. The compliment of the product of two variables equals the sum of the compliment of those variables.

Circuit designing for simple Boolean expressions:
By using basic gates such as AND, OR and NOT gates we can create logic circuits.

Universal gates:
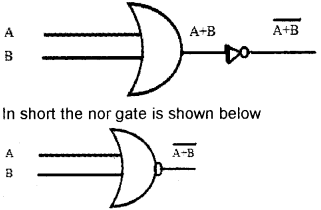
By using NAND and NOR gates only we can create other gates hence these gates are called Universal gate.

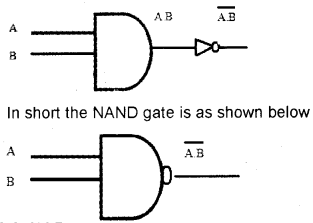
NAND gate:
The output of AND gate is inverted by NOT gate is the NAND gate

NOR gate:
The output of OR gate is inverted by NOT gate is the NOR gate.

Plus One Computer Science Notes