ML Aggarwal ICSE Solutions for Class 6 Maths Chapter 11 Understanding Symmetrical Shapes
ML Aggarwal SolutionsICSE SolutionsSelina ICSE Solutions
ML Aggarwal ICSE Solutions for Class 6 Maths Chapter 11 Understanding Symmetrical Shapes Exercise 11.1
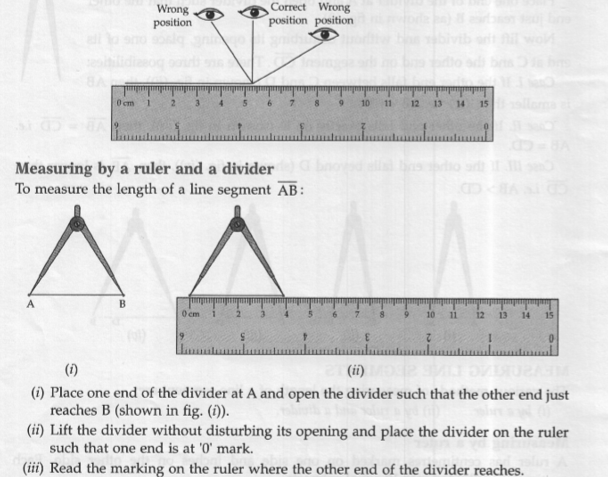
Solution 01:
It gives accurate measurement and avoids error due to thickness of ruler or positioning of eye (due to angular viewing)
Solution 02:
By measuring the lengths of the given figure
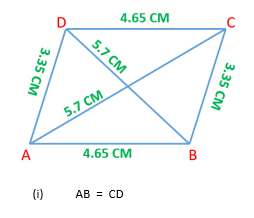
(i) AB = CD
(ii) BC < AB
(iii) AC = BD
(iv) CD < BD
Solution 03:
Given that AC = 10 CM, AB = 6 CM and BC = 4 CM
By constructing line segment by the given data, the model drawn as below.

Point B lies in between A and C
Solution 04:

By measuring the Lengths of line segments in the above figure
AB = 3 CM
BC = 1.5 CM
(i) It can be observed that AC = AB + BC [i.e. 4.5 CM = 3 CM + 1.5 CM]
(ii) AC – BC = AB 4.5 CM – 1.5 CM = 3 CM by measurement fount that AB = 3 CM, so AC – BC = AB.
Solution 05:
By measuring the lengths of the given figure.

Given data
AB = 1.9 CM
BC = 0.7 CM
CD = 1.9 CM
AD = 4.5 CM
(i) AC + BD = 2.6 CM + 2.6 CM = 5.2 CM AD + BC = 4.5 CM + 0.7 CM = 5.2 CM Hence, AC + BD = AD +BC.
(ii) AB + CD = 1.9 CM + 1.9 CM = 3.8 CM AD – BC = 4.5 CM – 0.7 CM = 3.8 CM Hence, AC + BD = AD +BC.
Solution 06:
By measuring the lengths of the given triangle ABC as below
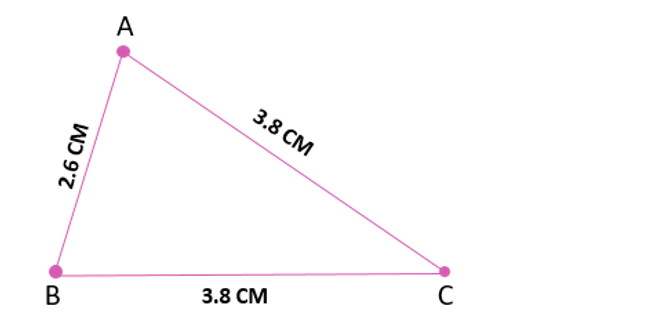
AB = 2.6 CM, AC = 3.8 CM and BC = 3.8 CM.
(i) AB + BC = 2.6 CM + 3.8 CM = 6.4 CM AC = 3.8 CM Hence, AB + BC > AC.
(ii) BC + AC = 3.8 CM + 3.8 CM = 7.6 CM AB = 2.6 CM Hence, AB > BC + AC.
(iii) AC + AB = 3.8 CM + 2.6 CM = 5.4 CM BC = 3.8 CM Hence, AC + AB > BC.
ML Aggarwal ICSE Solutions for Class 6 Maths Chapter 11 Understanding Symmetrical Shapes Exercise 11.2
Solution 01:
(i) When the hour hand moves from 4 to 10 clockwise, fraction of revolution turned = ½ Number of right angles turned = 2.
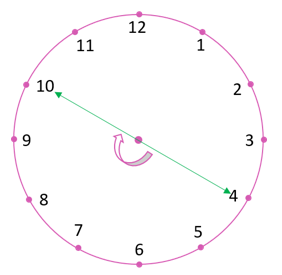
(ii) When the hour hand moves from 2 to 5 clockwise, fraction of revolution turned = ¼. Number of right angles turned = 1.
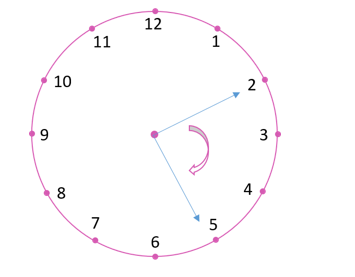
(iii) When the hour hand moves from 7 to 10 clockwise, fraction of revolution turned = ¼. Number of right angles turned = 1.
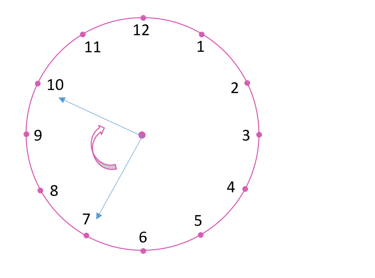
(iv) When the hour hand moves from 8 to 5 clockwise, fraction of revolution turned = ¾. Number of right angles turned = 3.
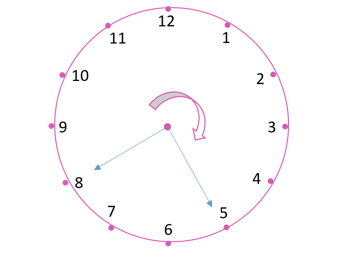
(v) When the hour hand moves from 11 to 5 clockwise, fraction of revolution turned = ½ Number of right angles turned = 2.
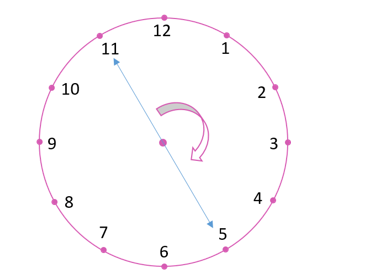
(vi) When the hour hand moves from 6 to 3 clockwise, Fraction of revolution turned = ¾. Number of right angles turned = 3.
Solution 02:
(i) When the hour hand moves from 10 and makes half revolution, clockwise it will stop at 4.

(ii) When the hour hand moves from 4 and makes 1/4 revolution, clockwise it will stop at 7.
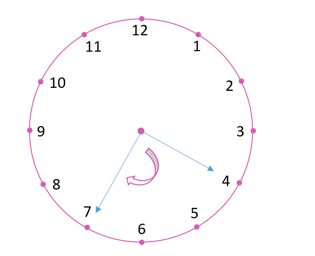
(iii) When the hour hand moves from 4 and makes 3/4 revolution, clockwise it will stop at 1.
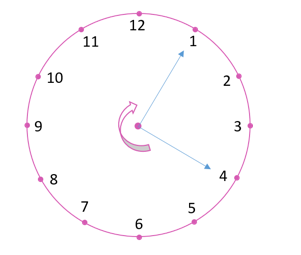
Solution 03:
(i) When the hour hand moves from 6 and turns through 1 right angle, clockwise it will stop at 9.
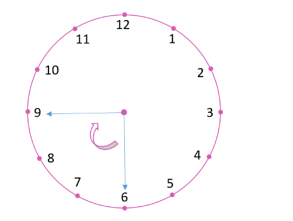
(ii) When the hour hand moves from 8 and turns through 2 right angles, clockwise it will stop at 2.
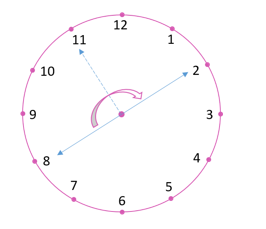
(iii) When the hour hand moves from 10 and turns through 3 right angles, clockwise it will stop at 7.
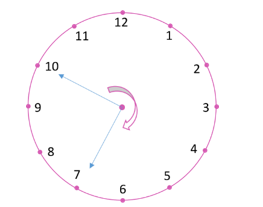
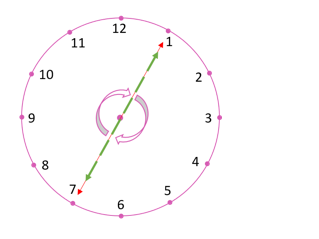
(iv) When the hour hand moves from 7 and turns through 2 straight angles, clockwise it will stop at 7.
Solution 04:
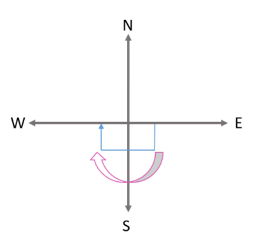
(i) While turning from north to south Fraction of a revolution = ¾. Number of right angles = 3.
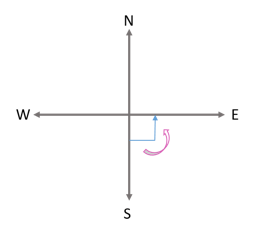
(ii) While turning from south to east Fraction of a revolution = 1/4. Number of right angles = 1.
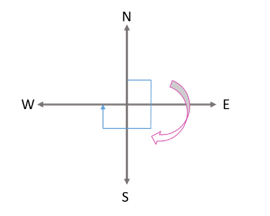
(iii) While turning from east to west (clockwise). Fraction of a revolution = 1/2. Number of right angles = 2.
Solution 05:
(i) Straight angle – (c) Half of a revolution
(ii) Right angle – (d) One fourth of a revolution
(iii) Complete angle – (f) One complete revolution
(iv) Acute angle – (b) Less than one fourth of a revolution
(v) Obtuse angle – (e) Between ¼ and ½ of a revolution
(vi) Reflex angle – (a) More than half of a revolution
Solution 06:
(i) Acute angle
(ii) Obtuse angle
(iii) Right Angle
(iv) Straight angle
(v) Reflex angle
(vi) Reflex angle
(vii) Acute angle
(viii) Obtuse angle
Solution 07:
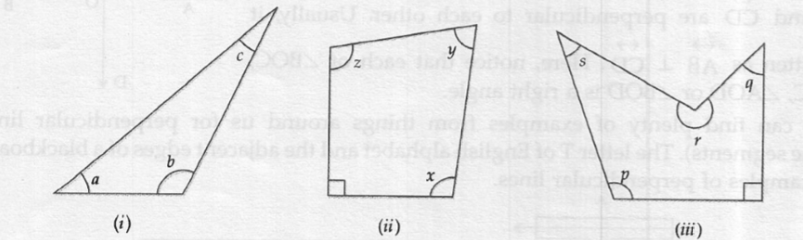
(i) Angle a and Angle c are acute, Angle b is obtuse
(ii) Angle x and Angle z are Obtuse, Angle y is acute
(iii) Angle p is obtuse, Angle q and Angle s are acute and Angle r is reflex.
Solution 08:

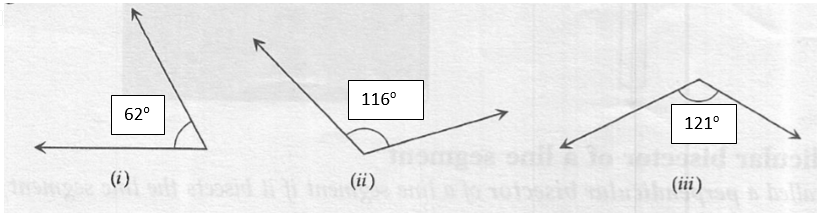
By measuring the protractor marked angles are as follows
(i) 62o
(ii) 116o
(iii) 121o
Solution 09:

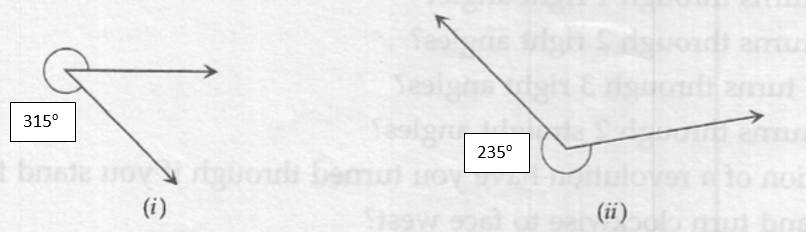
By measuring the protractor marked angles are as follows
(i) 315o
(ii) 235o
Solution 10:
In the clock the angle between every numeric is 30o i.e. angle between 1 and 2 is 30o, 2 and 3 is 30o and 4 and 6 is 30o x 2 = 60o
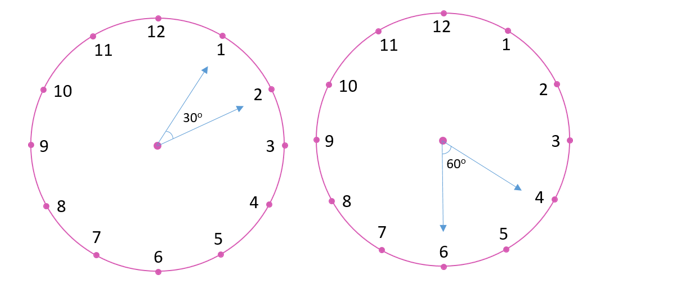
Similarly,
(i) Angle between the hands of the clock – 60o
(ii) Angle between the hands of the clock – 30o

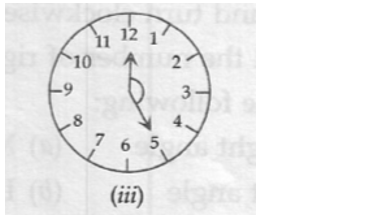
(iii) Angle between the hands of the clock – 150o
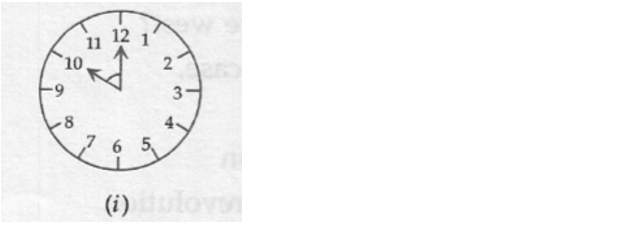
Solution 011:
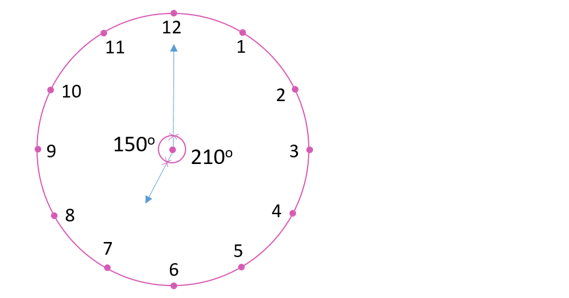
Smaller angle formed by the hour and minutes hands of a clock at 7’O clock is 150o [30o x 5 = 150o] (Type of Angle – Obtuse angle) as shown in the above model
Other Angle = 360o – 150o = 210o (Type of Angle – Reflex angle)
Solution 12:
One is a 30o – 60o – 90o set square; the other is a 45o – 45o -90o set square. The angle of measure 90o is common between them.
ML Aggarwal ICSE Solutions for Class 6 Maths Chapter 11 Understanding Symmetrical Shapes Exercise 11.3
Solution 01:
Two straight line are called perpendicular lines if they intersect at right angles.
In the given models (i), (iii) and (iv) are perpendicular lines.
Solution 02:
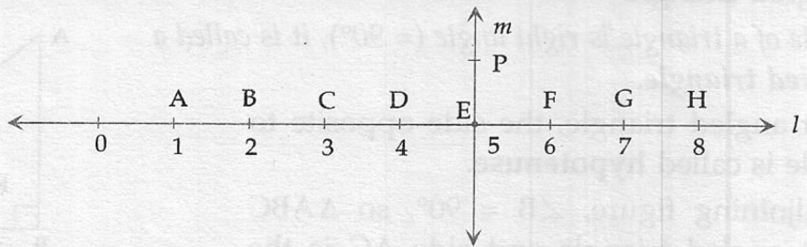 (i) Yes, CE = EG; E is the midpoint of CG
(i) Yes, CE = EG; E is the midpoint of CG
(ii) Yes, PF Line bisect segment BH – E is the midpoint of BH and Line P bisects line segment BH.
(iii) Line segment DF, Line segment BH
(iv) All are true (AC > FG, CD = GH and BC < EG)
ML Aggarwal ICSE Solutions for Class 6 Maths Chapter 11 Understanding Symmetrical Shapes Exercise 11.4
Solution 01:
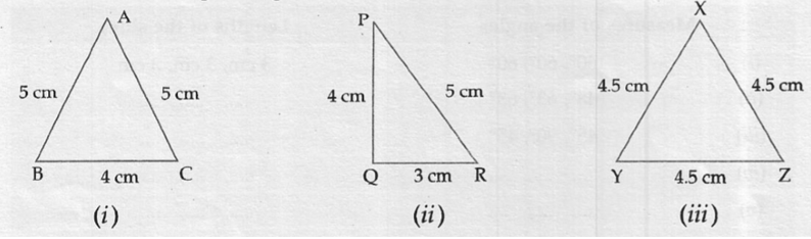
(i) Two sides are equal – Isosceles triangle
(ii) Three sides are different – Scalene triangle
(iii) Three sides are equal – Equilateral triangle
Solution 02:
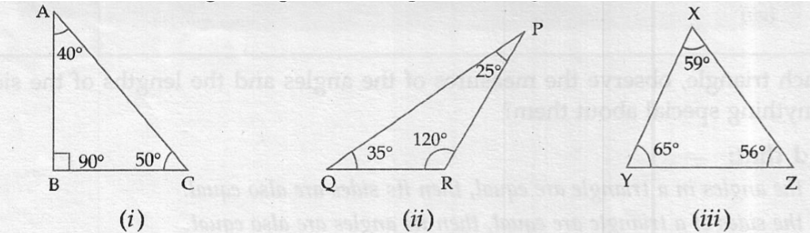
(i) Angle is 90o – Right angled triangle
(ii) Angle is more than 90o – Obtuse angled triangle
(iii) Angle is less than 90o – acute angled triangle
Solution 03:
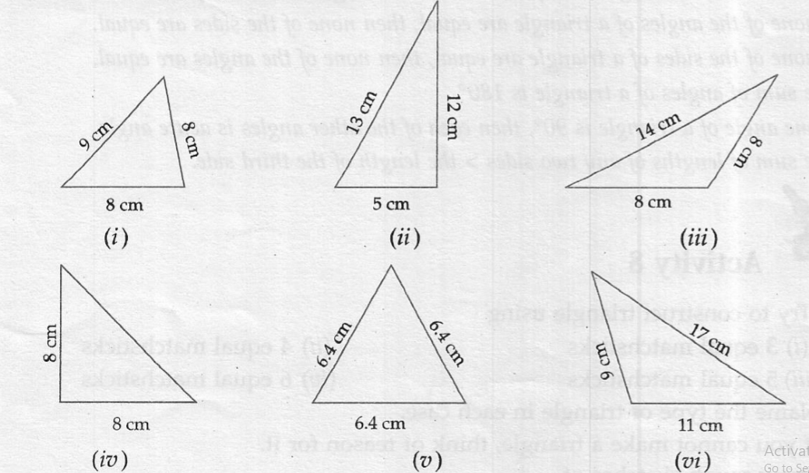
(i) Angle is less than 90o – acute angled triangle and two sides are in equal in length- Isosceles triangle.
(ii) Angle is 90o – right angled triangle and three sides are in not equal in length- scalene triangle.
(iii) Angle is more than 90o – Obtuse angled triangle and two sides are in equal in length- Isosceles triangle.
(iv) Angle is 90o – right angled triangle and two sides are equal in length- Isosceles triangle.
(v) Angle is less than 90o – acute angled triangle and three sides are in equal in length- Equilateral triangle.
(vi) Angle is more than 90o – Obtuse angled triangle and three sides are in not equal in length- scalene triangle.
Solution 04:
(i) Three sides of equal length – (e) Equilateral
(ii) 2 Sides of length – (g) Isosceles
(iii) All sides of different length – (a) Scalene
(iv) 3 acute angles – (f) Acute angled
(v) 1 right angle – (d) Right Angled
(vi) 1 Obtuse angle- C) Obtuse Angled
(vii) 1 Right angle with two sides of equal length – (b)Right angled Isosceles
Solution 05:
(i) False
(ii) True
(iii) True
(iv) False
(v) False
(vi) False
(vii) True
(viii) False
ML Aggarwal ICSE Solutions for Class 6 Maths Chapter 11 Understanding Symmetrical Shapes Exercise 11.5
Solution 01:
(i) True
(ii) True
(iii) True
(iv) True
(v) False
(vi) False
(vii) False
Solution 02:
(i) Not a polygon, because it is not a closed curve
(ii) Polygon, because it is a simple closed curve made up entirely of line segments
(iii) Not a polygon, because it is not a simple curve
(iv) Not a polygon, because it is not made up of entirely line segments.
Solution 03:
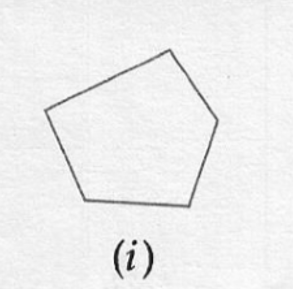
(i) Pentagon
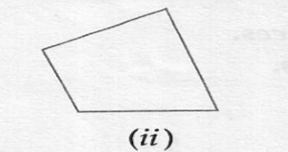
(ii) Quadrilateral
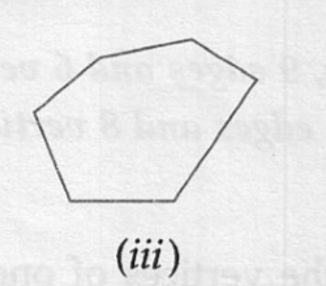
(iii) Hexagon
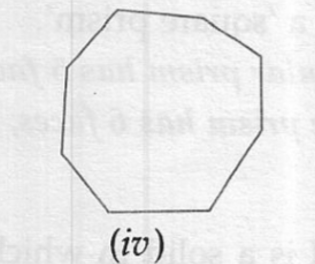
(iv) Octagon
Solution 04:
ABCDE is a regular pentagon and diagonals as in the below figure.
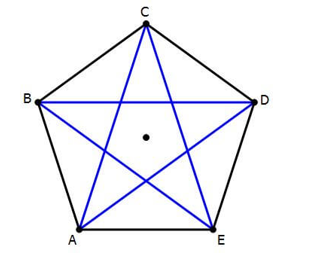
Solution 05:
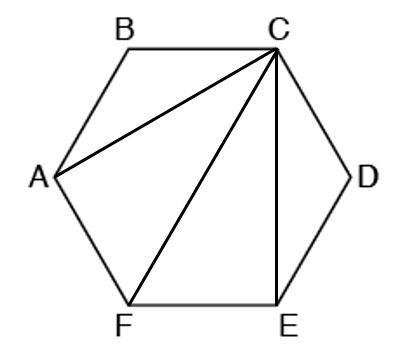
Let ABCDEF be regular hexagon then
(i) Triangle ABC is an Isosceles triangle.
(ii) Triangle CEF is a right angled triangle.
Solution 06:
ABCD is a regular quadrilateral – Square.
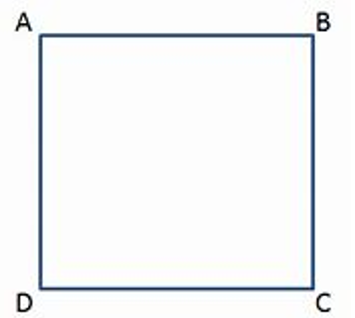
ML Aggarwal ICSE Solutions for Class 6 Maths Chapter 11 Understanding Symmetrical Shapes Exercise 11.6
Solution 01:
(i) Cuboid
(ii) Cuboid
(iii) Cuboid
(iv) Cylinder
(v) Cube
(vi) Sphere
Solution 02:
(i) Cone
(ii) Sphere
(iii) Cube
(iv) Pyramid
(v) Cylinder
(vi) Cuboid
Solution 03:
(i) A cube has 6 square faces, 12 edges and 8 vertices.
(ii) A triangular prism has 2 triangular faces, 3 rectangular faces, 9 edges and 6 vertices.
(iii) A triangular pyramid has 4 faces, 6 edges and 4 vertices.
