ML Aggarwal Class 9 Simultaneous Linear Equations Chapter Test

ML Aggarwal Class 9 Solutions Chapter 5 Chapter Test

Solve the following simultaneous linear equations (1 to 4):
Question 1.
(i) 2x – \(\frac {3}{4}\) y = 3, 5x – 2y = 7
Answer:

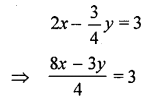
⇒ 8x – 3y = 3 × 4
⇒ 8x – 3y = 12 (1)
and 5x – 2y = 7 (2)
Multiplying equation (1) by 2 and equation (2) by 3, we get

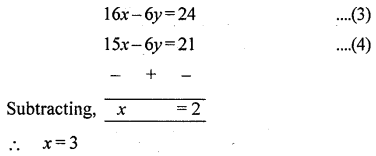
Substituting the value of x in equation (2), we get
5 × 3 – 2y = 7
⇒ 15 – 2y = 7
⇒ 15 – 7 = 2y
⇒ 2y = 8
⇒ y = \(\frac {8}{2}\)
⇒ y = 4
Hence, x = 3, y = 4

(ii) 2(x – 4) = 9y + 2, x – 6y = 2
Answer:
2(x – 4) = 9y + 2 …(1)
x – 6y = 2 …(2)
Now, 2 (x – 4) = 9y + 2 ⇒ 2x – 8 = 9y + 2
⇒ 2x – 9y = 2 + 8 ⇒ 2x – 9y = 10
Multiplying equation (2) by 2, we get

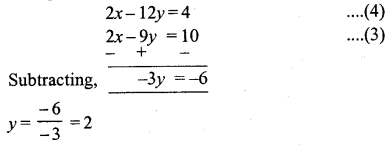
Substituting the value of y in equation (2) we get
x – 6 × 2 = 2 ⇒ x – 12 = 2 ⇒ x = 2 + 12
⇒ x = 14
Hence, x = 14, y = 2.

Question 2.
(i) 97x + 53y = 177, 53x + 97y = 573
Answer:
97x + 53y = 177 ……..(1)
And 53x + 97y = 573 ………..(2)
Multiplying equation (1) by 53 and equation (2) by 97, we get

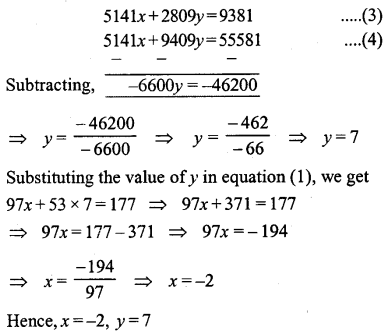
(ii) x + y = 5.5, x – y = 0.9
Answer:

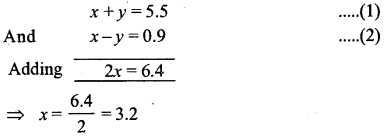
Substituting the value of x in equation (1), we get
3.2 + y = 5.5 ⇒ y = 5.5 – 3.2 ⇒ y = 23
Hence, x = 3.2, y = 2.3

Question 3.
(i) x + y = 7xy, 2x – 3y + xy = 0
Answer:
x + y = 7xy

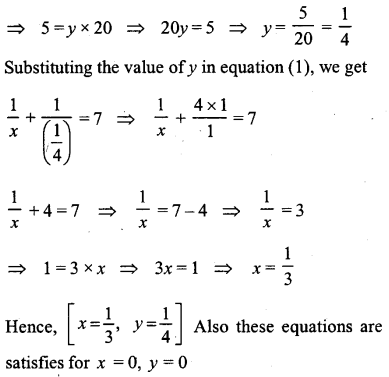
(ii)

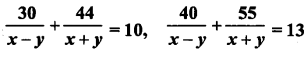
Answer:

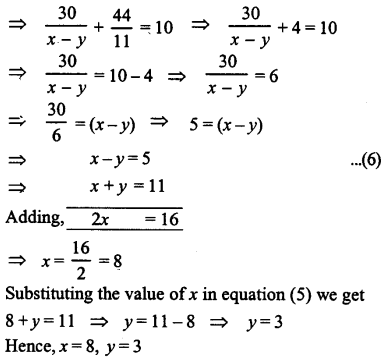
Question 4
(i) ax + by = a – b, bx – ay = a + b
Answer:
ax + by = a – b (1)
bx – ay = a + b (2)
Multiplying equa. (1), by a and equa. (2) by b, we get

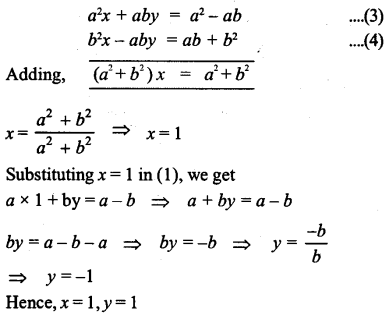
(ii) 3x + 2y = 2xy

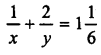
Answer:

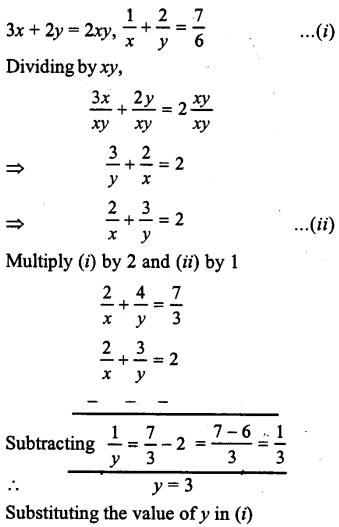
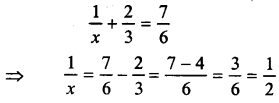
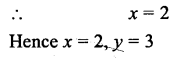
Question 5.
Solve 2x = \(\frac{3}{y}\) =9, 3x + \(\frac{7}{y}\) = 2. Hence find the value of k if x = ky + 5.
Answer:
Given equations

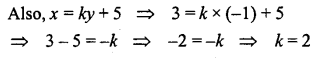
Question 6.
Solve:

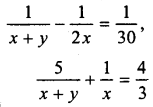
Hence f find the value of 2x² – y².
Answer:
Let x + y = a, then

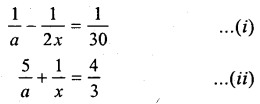
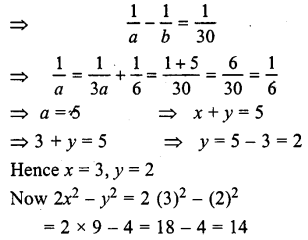
Question 7.
Can x, y be found to satisfy the following equations simultaneously ?

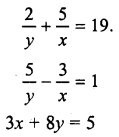
If so, then find
Answer:



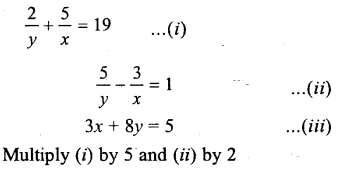
which in true
Hence the given three equations are simulteneously

ML Aggarwal Class 9 Solutions for ICSE Maths