ML Aggarwal Class 9 Solutions for ICSE Maths Chapter 11 Mid Point Theorem Chapter Test
Question 1.
ABCD is a rhombus with P, Q and R as mid¬points of AB, BC and CD respectively. Prove that PQ ⊥ QR.
Answer:
Given : ABCD is a rhombus with P, Q and R as mid-points of AB, BC and CD respectively.
To Prove: PQ ⊥ QR
Construction : Join AC & BD.
Proof : Diagonals of rhombus intersect at right angle.
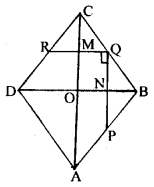
∴ ∠MON = 90°
In ∆BCD
Q and R are mid-points of BC and CD respectively.
∴ RQ || DB and RQ = \(\frac{1}{2}\) DB …..(2)
∴ RQ || DB ⇒ MQ || ON
∴ ∠MQN + ∠MON = 180°
⇒ ∠MQN + 90°= 180° ⇒ ∠MQN = 180°-90°
⇒ ∠MQN = 90° ⇒ NQ ⊥ MQ
or PQ ⊥ QR (Q.E.D.)
Question 2.
The diagonals of a quadrilateral ABCD are perpendicular. Show that the quadrilateral formed by joining the mid-points of its adjacent sides is a rectangle.
Answer:
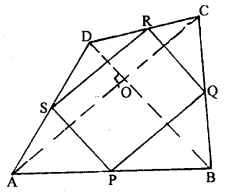
Given : ABCD is a quadrilateral in which diagonals AC and BD are perpendicular to each other. P, Q, R and S are mid-points of AB, BC, CD and DA respectively.
To prove: PQRS is a rectangle.
Proof : P and Q are mid-points of AB and BC (given)
∴ PQ || AC and PQ = \(\frac{1}{2}\) AC ….(1)
Again S and R are mid-points of AD and DC (given)
∴ SR || AC and SR = \(\frac{1}{2}\) AC ….(2)
From (1) and (2)
PQ || SR and PQ = SR
∴ PQRS is a parallelogram
Further AC and BD intersect at right angles
∴ SP || BD and BD ⊥ AC.
∴ SP ⊥ AC
i.e. SP ⊥ SR
i.e. ∠RSP =90″
∴ ∠RSP = ∠SRQ – ∠RQS = ∠SPQ = 90°
∴ PQRS is a rectangle (Q.E.D.)
Question 3.
If D, E, F are mid-points of the sides BC, CA and AB respectively of a ∆ ABC, Prove that AD and FE bisect each other.
Answer:
Given : D, E, F are mid-points of the sides BC, CA and AB respectively of a ∆ ABC
To Prove: AD and FE bisect each other.
Const: Join ED and FD
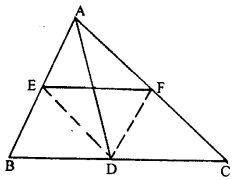
Proof : D and E are mid-points of BC and AB respectively (given).
∴ DE || AC ⇒ DE || AF ….(1)
Again D and F are mid-points of BC and AC respectively (given)
∴ DF || AB ⇒ DF || AE …..(2)
From (1) and (2)
ADEF is a ||gm
∵ Diagonals of a ||gm bisect each other
∴ AD and EF bisect each other.
Hence, the result. (Q.E.D.)
Question 4.
In ∆ABC, D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F. Prove that BDEF is a parallelogram. If AB = 8 cm and BC = 9 cm, find the perimeter of the parallelogram BDEF.
Answer:
Given. In ∆ABC, D and E are the mid-points of sides AB and AC respectively. DE is joined and from E, EF || AB is drawn AB = 8 cm and BC = 9cm.
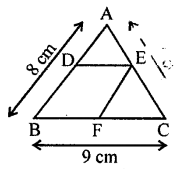
To prove.
(i) BDEI is a parallelogram.
(ii) Find the perimeter of BDEF
Proof: In ∆ABC,
∵ B and E are the mid-points of AB and AC respectively
∴ DE || BC and DE = \(\frac{1}{2}\)BC
∵ EF || AB
∴ DEFB is a parallelogram.
∴ DE = BF
∵ DE = \(\frac{1}{2}\) BC = \(\frac{1}{2}\) × 9 = 4·5 cm
EF = \(\frac{1}{2}\) AB = \(\frac{1}{2}\) × 8 = 4 cm.
∴ Perimeter of BDEF = 2 (DE + EF)
=2 (4·5 + 4)
= 8·5 × 2 = 17 cm.
Question 5.
In the given figure, ABCD is a parallelogram and E is mid-point of AD. DL || EB meets AB produced at F. Prove that B is mid-point of AF and EB = LF.
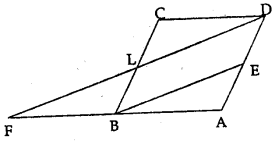
Solution:
Given : In the given figure,
ABCD is a parallelogram
E is mid-point of AD
DL || EB meets AB produced at F
To prove : EB = LF
B is mid-point of AF
Proof: ∵ BC || AD and BE || LD
∴ BEDL is a parallelogram
∴ BE = LDandBL = AE
∵ E is mid-point of AD
∴ L is mid-point of BC
In ∆FAD,
E is mid-point of AD and BE || LD at FLD
∴ B is mid point of AF
∵ EB = \(\frac{1}{2}\) FD = LF
Question 6.
In the given figure, ABCD is a parallelogram. If P and Q are mid-points of sides CD and BC respectively. Show that CR = \(\frac{1}{4}\) AC.
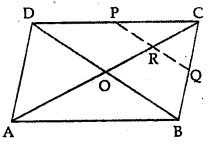
Solution:
Given : In the figure, ABCD is a parallelogram P and Q are the mid-points of sides CD and BC respectively.
To prove : CR = \(\frac{1}{4}\) AC
Construction : Join AC and BD.
Proof: In ||gm ABCD, diagonals AC and BD bisect each other at O
AO = OC or OC = \(\frac{1}{2}\) AC …….(i)
In ∆BCD,
P and Q are mid points of CD and BC
∴ PQ || BD
∵ In ∆BCO,
Q is mid-point of BC and PQ || OB
∴ R is mid-point of CO
∴ CR = \(\frac{1}{2}\) OC = \(\frac{1}{2}\) (\(\frac{1}{2}\)BC)
∴ CR = \(\frac{1}{4}\)BC