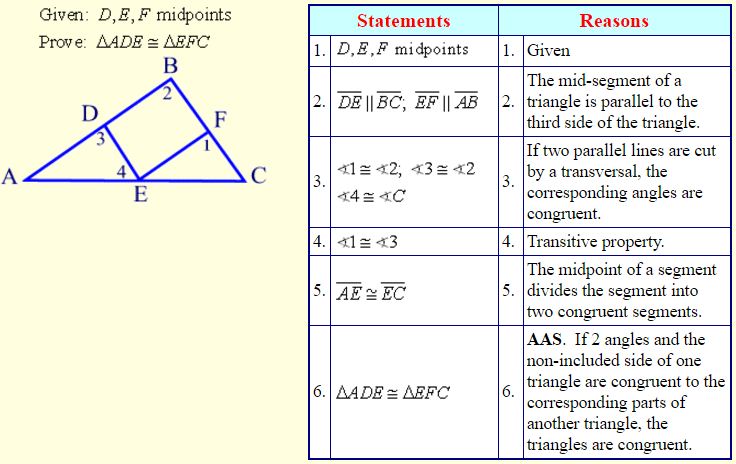
Mid-Segment of a Triangle

Mid-Segment of a Triangle

Definition:
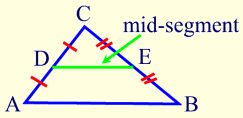
The mid-segment of a triangle (also called a midline) is a segment joining the midpoints of two sides of a triangle.

Properties:

1. The mid-segment of a triangle joins the midpoints of two sides of a triangle such that it is parallel to the third side of the triangle.
2. The mid-segment of a triangle joins the midpoints of two sides of a triangle such that its length is half the length of the third side of the triangle.

Examples:

1. Given DE is the length of the mid-segment. Find AB.
   
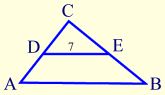
   Solution:
   The mid-segment is half of the third side.
   7 is half of 14.
   AB = 14.
2. Given DE, DF, and FE are the lengths of mid-segments. Find the perimeter of triangle ABC.
   
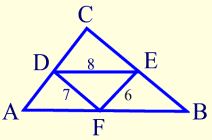
   Solution:
   The mid-segment is half of the third side.
   6 is half of 12 so AC = 12
   7 is half of 14 so CB = 14
   8 is half of 16 so AB = 16
   The perimeter of the large triangle ABC is:
   12 + 14 + 16 = 42.
3. .