Matrices

Matrices

Definition
A rectangular arrangement of numbers (which may be real or complex numbers) in rows and columns, is called a matrix. This arrangement is enclosed by small ( ) or big [ ] brackets. The numbers are called the elements of the matrix or entries in the matrix.

Order of a matrix

A matrix having m rows and n columns is called a matrix of order m×n or simply m×n matrix (read as an m by n matrix). A matrix A of order m×n is usually written in the following manner:

A matrix of order m × n contains mn elements. Every row of such a matrix contains n elements and every column contains m elements.

Equality of matrices

Two matrix A and B are said to be equal matrix if they are of same order and their corresponding elements are equal.

Types of matrices

https://www.youtube.com/watch?v=nfG4NwLhH14

1. Row matrix: A matrix is said to be a row matrix or row vector if it has only one row and any number of columns. Example: [5 0 3] is a row matrix of order 1× 3 and [2] is a row matrix of order 1×1.
2. Column matrix: A matrix is said to be a column matrix or column vector if it has only one column and any number of rows.
   Example: \(\left[ \begin{matrix} 2 \\ 3 \\ -6 \end{matrix} \right]\) is a column matrix of order 3 × 1 and [2] is a column matrix of order 1 × 1. Observe that [2] is both a row matrix as well as a column matrix.
3. Singleton matrix: If in a matrix there is only one element then it is called singleton matrix.
   Thus, A = [a_ij]_m×n is a singleton matrix, if m = n =1
   Example: [2], [3], [a], [–3] are singleton matrices.
4. Null or zero matrix: If in a matrix all the elements are zero then it is called a zero matrix and it is generally denoted by O. Thus A = [a_ij]_m×n is a zero matrix if a_ij = 0 for all i and j.
   Example: \(\left[ 0 \right] ,\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix},\left[ \begin{matrix} 0 & 0 & 0 \\ 0 & 0 & 0 \end{matrix} \right] ,\left[ \begin{matrix} 0 & 0 \end{matrix} \right]\) are all zero matrices, but of different orders.
5. Square matrix: If number of rows and number of columns in a matrix are equal, then it is called a square matrix.
   Thus A = [a_ij]_m×n is a square matrix if m = n.
   Example: \(\left[ \begin{matrix} { a }_{ 11 } & { a }_{ 12 } & { a }_{ 13 } \\ { a }_{ 21 } & { a }_{ 22 } & { a }_{ 23 } \\ { a }_{ 31 } & { a }_{ 32 } & { a }_{ 33 } \end{matrix} \right]\) is a square matrix of order 3×3.
   (i) If m ≠ n then matrix is called a rectangular matrix.
   (ii) The elements of a square matrix A for which i = j, i.e. a₁₁, a₂₂, a₃₃, ….. a_mn are called diagonal elements and the line joining these elements is called the principal diagonal or leading diagonal of matrix A.
6. Diagonal matrix: If all elements except the principal diagonal in a square matrix are zero, it is called a diagonal matrix. Thus a square matrix A = [a_ij] is a diagonal matrix if a_ij ≠ 0 when i ≠ j.
   Example: \(\left[ \begin{matrix} 2 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 4 \end{matrix} \right]\) is a diagonal matrix of order 3× 3, which can be denoted by diag [2, 3, 4].
7. Identity matrix: A square matrix in which elements in the main diagonal are all ‘1’ and rest are all zero is called an identity matrix or unit matrix. Thus, the square matrix A = [a_ij] is an identity matrix, if
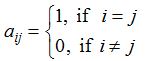
   We denote the identity matrix of order n by I_n.
   Example: \(\left[ 1 \right] ,\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix},\left[ \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix} \right]\) are identity matrices of order 1, 2 and 3 respectively.
8. Scalar matrix: A square matrix whose all non diagonal elements are zero and diagonal elements are equal is called a scalar matrix. Thus, if A = [a_ij] is a square matrix and 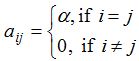, then A is a scalar matrix.
   Unit matrix and null square matrices are also scalar matrices.
9. Triangular matrix: A square matrix [a_ij] is said to be triangular matrix if each element above or below the principal diagonal is zero. It is of two types
   (i) Upper triangular matrix: A square matrix [a_ij] is called the upper triangular matrix, if a_ij = 0 when i > j.
   Example: \(\left[ \begin{matrix} 3 & 1 & 2 \\ 0 & 4 & 3 \\ 0 & 0 & 6 \end{matrix} \right] \) is an upper triangular matrix of order 3 × 3.
   (ii) Lower triangular matrix: A square matrix [a_ij] is called the lower triangular matrix, if a_ij = 0 when i< j.
   Example: \(\left[ \begin{matrix} 1 & 0 & 0 \\ 2 & 3 & 0 \\ 4 & 5 & 2 \end{matrix} \right]\) is a lower triangular matrix of order 3 × 3.

Trace of a matrix

The sum of diagonal elements of a square matrix. A is called the trace of matrix A , which is denoted by tr A.

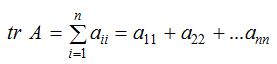
Properties of trace of a matrix
Let A = [a_ii]_n×n  and B = [b_ij]_n×n and λ be a scalar

1. tr(λA) = λ tr(A)
2. tr(A – B) = tr(A) – tr(B)
3. tr(AB) = tr(BA)
4. tr(A)= tr(A’) or tr (A^T)
5. tr(I_n) = n
6. tr (0)= 0
7. tr(AB) ≠ trA.trB

Addition and subtraction of matrices

If A = [a_ij]_m×n  and B = [b_ij]_m×n are two matrices of the same order then their sum A+B is a matrix whose each element is the sum of corresponding elements i.e., A + B = [a_ij + b_ij]_m×n.
Similarly, their subtraction is defined as A – B = [a_ij – b_ij]_m×n

Matrix addition and subtraction can be possible only when matrices are of the same order.
Properties of matrix addition : If A, B and C are matrices of same order, then

1. A + B = B + A (Commutative law)
2. (A + B) + C = A + (B + C) (Associative law)
3. A + O = O + A = A, where O is zero matrix which is additive identity of the matrix.
4. A + (–A) = O = (–A) + A , where (–A) is obtained by changing the sign of every element of A, which is additive inverse of the matrix.
5.