A Plus Topper

Improve your Grades

Math Labs with Activity - Verify the Properties of the Diagonals of a Parallelogram

by

Math Labs with Activity – Verify the Properties of the Diagonals of a Parallelogram

OBJECTIVE

To verify the properties of the diagonals of a parallelogram

Materials Required

  1. A sheet of white paper
  2. A sheet of glazed paper
  3. A geometry box
  4. A pair of scissors

Theory
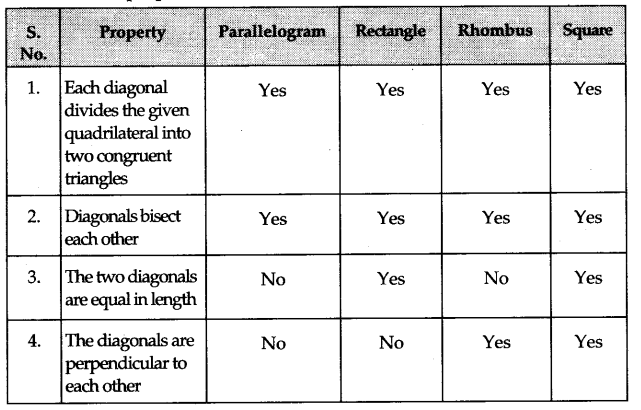
By geometry, we know that

  1. a diagonal of a parallelogram divides it into two congruent triangles, and
  2. the diagonals of a parallelogram bisect each other.

Procedure
Step 1: Construct a parallelogram ABCD on the sheet of white paper.
Step 2: Draw the diagonal AC of the parallelogram.
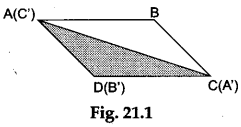
Step 3: Make an exact copy of ΔABC on the glazed paper. Label it as ΔA’B’C’. Cut ΔA’B’C formed on the glazed paper.
Step 4: Rotate ΔA’B’C’ formed on the glazed paper and place it over the ΔACD as shown in Figure 21.1. Record your observations (see Observation 1).
Math Labs with Activity - Verify the Properties of the Diagonals of a Parallelogram 1
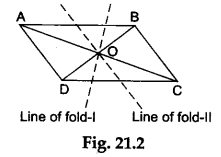
Step 5: Remove ΔA’B’C’. In the parallelogram ABCD draw the other diagonal BD.
Step 6: Mark the point O where the diagonals AC and BD intersect.
Step 7: Fold the paper along the line passing through the point O such that the line OA falls over the line OC as shown in Figure 21.2. Record your observations (see Observation 2).
Step 8: Fold the paper along the line passing through the point O such that the line OB falls over the line OD as shown in Figure 21.2. Record your observations (see Observation 3).
Math Labs with Activity - Verify the Properties of the Diagonals of a Parallelogram 2

Observations

  1. We observe that ΔA’B’C’ exactly covers ΔACD.
    Therefore, ΔA’B’C’ is congruent to ΔACD, i.e., ΔABC is congruent to ΔACD.
  2. During the first fold, when the line OA falls over the line OC, we observe that the point A falls exactly over the point C. This shows that OA = OC, i.e., point O is the midpoint of the diagonal AC. So, the diagonal BD bisects the diagonal AC.
  3. During the second fold, when the line OB falls over the line OD, we observe that the point B falls exactly over the point D. This shows that OB = OD, i.e., point O is the midpoint of the diagonal BD. So, the diagonal AC bisects the diagonal BD.

Result
It is verified that

  1. a diagonal of a parallelogram divides it into two congruent triangles, and
  2. the diagonals of a parallelogram bisect each other.

Math Labs with Activity - Verify the Properties of the Diagonals of a Parallelogram 3

Math Labs with ActivityMath LabsMath Lab ManualScience LabsScience Practical Skills