Math Labs with Activity - Verify the Identity (a² - b²) = (a+b)(a-b) (Method 2)

Math Labs with Activity – Verify the Identity (a² – b²) = (a+b)(a-b) (Method 2)

OBJECTIVE

To verify the identity (a² – b²) = (a+b)(a-b) (Method 2)

Materials Required

1. A piece of cardboard
2. A sheet of glazed paper
3. A sheet of white paper
4. A geometry box
5. A tube of glue
6. A pair of scissors

Procedure
We take any values of a and b such that a>b.
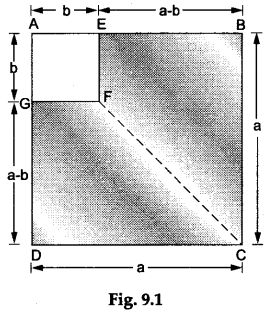
Step 1: Construct a square ABCD on the glazed paper such that each side of this square measures a units. Inside this square construct another square AEFG of side b units (where b < a) as shown in Figure 9.1. Join FC.

Step 2: Paste the sheet of white paper on the cardboard. Cut the two quadrilaterals EBCF and GFCD from the glazed paper and place them on the white sheet.

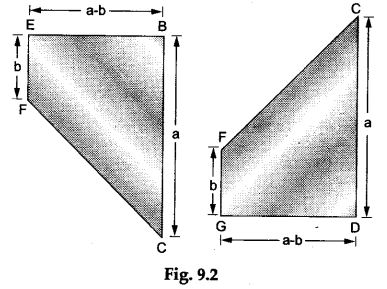
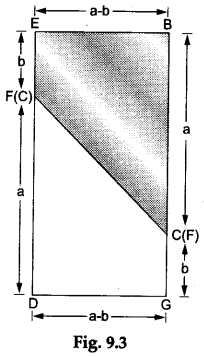
Step 3: Reverse the quadrilateral GFCD. Now paste the two quadrilaterals on the sheet of white paper to obtain the rectangle EBGD.

Observations and Calculations

1. In Figure 9.1, we have
   area of square ABCD = a² square units
   and area of smaller square AEFG =b² square units.
   ∴ area of quad. EBCF + area of quad. GFCD = area of square ABCD – area of square AEFG =(a² -b²) square units.
2. In Figure 9.3, we have
   area of rect. EBGD = (a+b)(a-b) square units.
   ∴ area of quad. EBCF + area of quad. GFCD =(a+b)(a-b) square units.
   Thus, from the above calculations we have (a² – b²) = (a+b)(a-b).

Result
The identity (a² – b²) = (a+b)(a-b) is verified geometrically.

Math Labs with ActivityMath LabsMath Lab ManualScience LabsScience Practical Skills