ISC Physics Question Paper 2013 Solved for Class 12

ISC Physics Previous Year Question Paper 2013 Solved for Class 12

Maximum Marks: 70
Time allowed: 3 hours

• Candidates are allowed additional 15 minutes for only reading the paper. They must NOT start writing during this time.
• Answer all questions in Part I and six questions from Part II, choosing two questions from each of the Sections A, B and C.
• All working, including rough work, should be done on the same sheet as, and adjacent to, the rest of the answer.
• The intended marks for questions or parts of questions are given in brackets [ ].
• Material to be supplied: Log tables including Trigonometric functions
• A list of useful physical constants is given at the end of this paper.

Part-I
(Answer all questions)

Question 1.
(A) Choose the correct alternative (a), (b), (c) or (d) for each of the questions given below : [5]
(i) Relative permittivity of water is 81. If ∈w and ∈0 are permitivities of water and vacuum respectively, then.
(a) \(\epsilon_{0}=9 \epsilon_{w}\)
(b) \(\epsilon_{0}=81 \epsilon_{w}\)
(c) \(\epsilon_{w}=9 \epsilon_{0}\)
(d) \(\epsilon_{w}=81 \epsilon_{0}\)

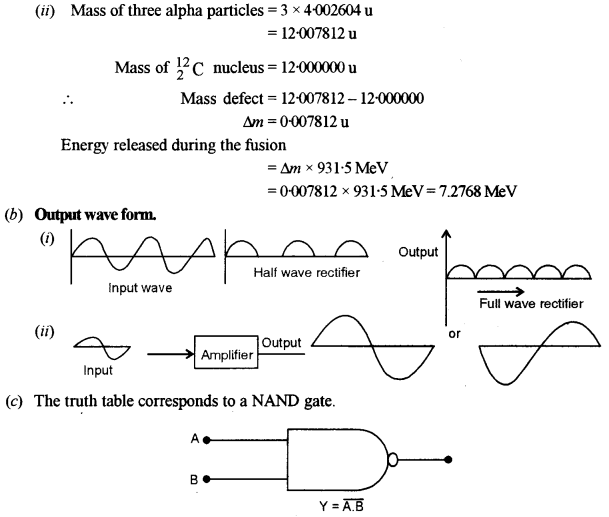
ii) Five resistors are connected as shown in figure. The effective resistance i.e., equivalent resistance between the points A and B is :
(a) 4 Ω
(b) 5 Ω
(c) 15 Ω
(d) 20 Ω

(iii) The Biot Savart’s Law in vector form is:
(a) \(\overline{\delta \mathrm{B}}=\frac{\mu_{0}}{4 \pi} \frac{d l(\overrightarrow{\mathrm{I}} \times \vec{r})}{r^{3}}\)
(b) \(\overline{\delta \mathrm{B}}=\frac{\mu_{0}}{4 \pi} \frac{\mathrm{I}(\overrightarrow{d l} \times \vec{r})}{r^{3}}\)
(c) \(\overline{\delta \mathrm{B}}=\frac{\mu_{0}}{4 \pi} \frac{\mathrm{I}(\vec{r} \times \overrightarrow{d l})}{r^{3}}\)
(d) \(\overline{\delta \mathrm{B}}=\frac{\mu_{0}}{4 \pi} \frac{\mathrm{I}(d \vec{l} \times \vec{r})}{r^{2}}\)

(iv) In an astronomical telescope of refracting type :
(a) Eyepiece has greater focal length
(b) Objective has greater focal length
(c) Objective and eyepiece have equal focal length
(d) Eyepiece has greater aperture than the objective.

(v) The particles which cannot be accelerated by a cyclotron or a Van de Graff generator are :
(a) Alpha particles
(b) Beta particles
(c) Neutrons
(d) Protons [15]

(B) Answer all questions given below briefly and to the point:
(i) A large hollow metallic sphere has a positive charge of 35.4 μC at its center. Find how much electric flux emanates from the sphere.

(ii) A current ‘I’ flows through a metallic wire of radius ‘r’ and the free electrons in it drift with a velocity v_d. Calculate the drift velocity of the free electrons through the wire of the same material, having double the radius, when same current flows through it.

(iii) Name any one instrument which works on the principle of tangent law in magnetism.

(iv) State the SI unit of magnetic dipole moment.

(v) Alternating current flowing through a certain electrical device leads over the potential difference across it by 90°. State whether this device is a resistor, capacitor or an inductor.

(vi) What is the shape of the wave front diverging from a point source of light ?

(vii) The critical angle for a given transparent medium and air is i_c. A ray of light travelling in air is incident on this transparent medium at an angle of incidence equal to the polarising angle i_p. What is the relation between the two angles i_c and i_p ?

(viii) Find the focal length and nature of a lens whose optical power is – 5D.

(ix) What is Modulation ? Explain in brief.

(x) What are the dark lines seen in the solar spectrum called ?

(xi) What is the relation between wavelength and momentum of moving particles ?

(xii) Name the series of lines in the hydrogen spectrum which lies in the ultra-violet region.

(xiii) Fill in the blank in the given nuclear reaction:
\(\begin{array}{r}{+\frac{27}{13} \mathrm{Al} \longrightarrow_{12}^{25} \mathrm{Mg}+\frac{4}{2} \mathrm{He}} \\ {13}\end{array}\)

(xiv) Give an example where energy is converted into matter.

(xv) To convert a pure semiconductor into n-type semiconductor, what type of impurity is added to it ?
Answer:
Answer.
(A) (i) (d)
(ii) (a)
(iii) (b)
(iv) (b)
(v) (c)

(B) (i) Here, q = 35.4 x 10^-6 C
By Gauss Law,
\(\phi=\frac{q}{\epsilon_{0}}=\frac{35 \cdot 4 \times 10^{-6}}{8 \cdot 85 \times 10^{-12}}=4 \times 10^{6} \mathrm{Nm}^{2} \mathrm{C}^{-1}\)

(ii) We know,

(iv) The SI unit of magnetic dipole moment is Coulomb-meter (Cm).
(v) The device is a capacitor.
(vi) Spherical.
(vii) If i_p is the polarising angle and n the refractive index of the medium, then n = tan i_p If i_c is the critical angle,then

(viii) We know that,
\(f_{m}=\frac{1}{\mathrm{D}}=-\frac{1}{5}=-0 \cdot 2 \mathrm{m}=-20 \mathrm{cm}\)
∴ – ve sign shows that the lens is concave.

(ix) The audio signal cannot be transmitted efficiently as such. Modulation is the process of modifying some characteristic of a high frequency carrier wave (amplitude, frequency or phase) in accordance with the instantaneous value of the amplitude of modulating signal. The modulating signal is then transmitted across space.

(x) Dark lines has also called Fraunhoffer’s lines.

(xi) The required relation is λ = h/p where λ = wavelength and p the momentum of the particle and h = Planck’s constant.

(xii) The series emitted in the hydrogen spectrums in ultra-violet region is called the “Lyman Series.”

(xiii) The missing particle is \(_{1}^{2} \mathrm{H}\)

(xiv) In pair production. It is materialization of energy.

(xv) To get n-type semiconductor, the semiconductor is doped with an impurity like antimony.

Part- II
(Answer any six questions in this part, choosing two questions from each of the Sections A, B and C)

Section-A
(Answer any six questions)

Question 2.
(a) (i) Write an expression (derivation not required) for intensity’ of electric field in :
(1) Axial position.
(2) Broad side position of an electric dipole, in terms of its length (2a) dipole moment (p) and distance (r).
(ii) What is the ratio of these two intensities i.e., E₁ : E₂, for a short electric dipole ? [3]

(b) Three capacitors C₁ = 6 μF, C₂ = 12 μF and C₃ = 20 μF are connected to a 100 V battery, as shown in figure alongside:

Calculate:
(i) Charge on each plate of capacitor C₁.
(ii) Electrostatic potential energy stored in capacitor C₃. [3]

(c) ‘n’ cells, each of emf’e and internal resistance ‘r’ are joined in series to form a row. ‘m’ such rows are connected in parallel to form a battery of N = mn cells. This battery is connected to an external resistance ‘R’. [3]
(i) What is the emf of this battery and how much is its internal resistance ?
(if) Show that current ‘I’ flowing through the external resistance R’ is given by :
\(\mathrm{I}=\frac{\mathrm{N} e}{m \mathrm{R}+n r}\)
Answer:




Question 3.
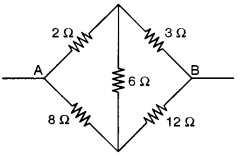
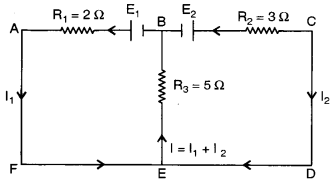
(a) In the circuit shown in figure, E₁ = 17 V, E₂ = 21V, R₁ = 2 Ω, R₂ = 3 Ω and R₃ = 5 Ω. Using Kirchhoff’s laws,find the currents flowing through the resistors R₁, R₂ and R₃. (Internal resistance of each of the batteries is negligible). [4]

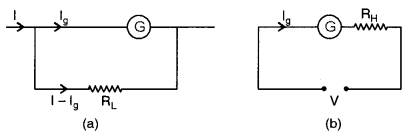
(b) You are provided with one low resistance R_L and one high resistance R_H and two galvanometers. One galvanometer is to be converted to an ammeter and the other to a voltmeter. Show how you will do this with the help of simple, labelled diagrams. [2]

(c) (i) Plot a labelled graph to show variation of thermo-emf ‘e’ versus temperature difference ‘θ’ between the two junctions of a thermo couple. Mark ‘N’ as neutral temperature and ‘I’ as temperature of inversion.
(ii) What is Peltier effect ? [3]
Answer:
(a) The distribution of current in the given circuit is as given below:
Apply first law at the point E



(b) A galvanometer is connected into an ammeter by connecting a low resistance of a suitable value in parallel with the galvanometer and into a voltmeter by connecting a high resistance in series with galvanometer as shown in fig. (a) and (b) respectively.

Question 4.
(a) Figure below shows two infinitely long and thin current carrying conductors X and Y kept in vacuum, parallel to each other, at a distance ‘a’. [2]

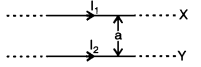
(i) How much force per unit length acts on the conductor Y due to the current flowing through X ? Write your answer in terms of (μ₀/4π), I₁, I₂ and a.
(Derivation of formula is not required.)
(ii) Define ampere, in terms of force between two current earning conductors.

(b) A metallic rod CD rests on a thick metallic wire PQRS with arms PQ and RS parallel to each other, at a distance l = 40 cm, as shown in figure. A uniform magnetic field B = 0.1 T acts perpendicular to the plane of this paper, pointing inwards (i.e,.. away from the reader). The rod is now made to slide towards right, with a constant velocity of v = 5 0 ms^-1. [3]

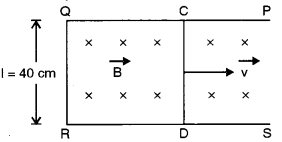
(i) How much emf is induced between the two ends of the rod CD ?
(ii) What is the direction in which the induced current flows.

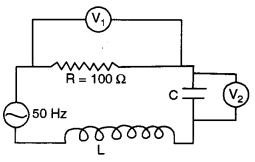
(c) (i) Figur below shows a series RCL circuit connected to an ac source which generates an alternating emf of frequency 50 Hz. The readings of the voltmeters V₁ and V₂ are 80 V and 60 respectively.

Find :
(1) the current in the circuit.
(2) the capacitance C of the capacitor.
(ii) At resonance, what is the relation between impedance of a series LCR circuit and its resistance R ?
Answer:
(a) (i) Two conductors X and Y of infinite length and separted by a distance ‘a’ carry currents I1 and I2 respectively. The force of attraction per unit length is given by
\(\frac{\mathrm{F}}{l}=\frac{\mu_{0}}{4 \pi} \frac{2 \mathrm{I}_{1} \mathrm{I}_{2}}{a}\)

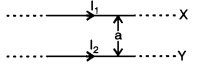
(ii) Definition of Ampere : 1 ampere is that much current which when flowing through each of the two infinitely long conductors separated by 1 m in vacuum results in a force 2 x 10-7 newton per meter length on each of them.

Section-B
(Answer any two questions)

Question 5.
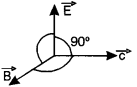
(a) (i) In an electromagnetic wave, how are electric vector \((\overrightarrow{\mathrm{E}})\), magnetic vector \((\overrightarrow{\mathrm{B}})\) and velocity of propagation of the wave \((\overrightarrow{\mathrm{C}})\) oriented ? [2]
(ii) How long wold gamma radiation take to travel from sun to earth, a distance of 1.5 x 10¹¹ m?

(b) With the help of a labelled diagram, show that fringe separation β in Young’s double slit experiment is given by : [4]
\(\beta=\frac{\lambda \mathrm{D}}{d}\)
where the terms have their usual meaning.

(c) (i) What is the difference between polarised light and unpolarised light based on the direction of electric vector \((\overrightarrow{\mathrm{E}})\) ?
(ii) What will be the effect on the width of the central bright fringe in the diffraction pattern of a single slift if:
(1) Monochromatic light of smaller wavelength is used.
(2) Slit is made narrower. [2]
Answer:

(b) In the fig. are shown two coherent sources S₁ and S₂ illuminated by the same source S.d is the distance between the two sources. D is the disance between the source and the screen. P is a point on the screen having an angle height θ. O is a point on the screen situated symmetrically w.r.t. two sources. Let OP = Y. Path difference between the disturbances starting from S₂ and Si reaching P. is
\(p=\mathrm{S}_{2} \mathrm{P}-\mathrm{S}_{1} \mathrm{P}\)



(c) (i) (1) In unpolarised light, the direction of the electric field vector is in any direction in a plane perpendicular to the direction of propagation.
(2) In polarised light, the direction of the electic vector is one particular direction perpendicular to the direction of propagation.
(ii) Width of the central maxima \(\left(2 \frac{\lambda}{a} \mathrm{D}\right)\) clearly :

• decreases when the wavelength is decreased.
• increases when the slit width V decreases.

Question 6.
(a) At what angle, a ray of light should be incident on the first face AB of a regular glass prism ABC so that the emergent ray grazes the adjacent face AC ? [3]

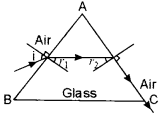
See figure alongside. (Refractive Index of glass = 1.6)

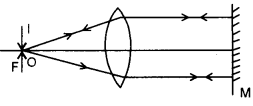
(b) A convex lens ‘L’ and a plane mirror ‘M’ are arranged as shown in figure below. Position of object pin ‘O’ is adjusted in such a way that the inverted image ‘I’ formed by the lens mirror combination, coincides with the object pin ‘O’. Explain how and when this happens. [2]

(c) Starting with an expression for refraction at a single spherical surface, obtain an expression for lens maker’s formula. [3]
Answer:


(b) When the object O is at the focus of the lens, the rays after refraction through the lens will be rendered parallel to the principal axis. These rays will strike the mirror normally and will retrace their path giving rise to an image, which will coincide with O as shown.

(c)

Consider a thin convex lens XY having R₁ and R₂ as the radii of curvatures of the two surfaces XP₁Y and XP₂Y respectively. Let n₁ be the refractive index of the medium in which the object O is situated and n₂ the refractive index of the material of the lens. The first surface of radius of curvature R₁ forms the image of the object O at a distance v’ from the surface XP₁Y. This image then serves as a virtual object for the second surface giving rise to a final image at I. For refraction at the first surface, we can write

Question 7.
(a) Show that the axial chromatic aberration (f_r – f_v) for a convex lens is equal to the product of its mean focal length (f) and dispersive power (ω) of its material i.e., Prove : [3]
f_r – f_v = ωf

(b) Draw a labelled diagram of an image formed by a compound microscope, with the image at least distance of distinct vision. Write any one expression for its magnifying power. [3]

(c) What is meant by long-sightedness ? How can this defect be corrected ? [2]
Answer:




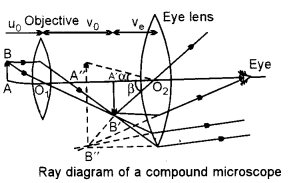
Here, μ₀ and v₀ are the objective distance and v₀ the image distance from the objective lens and D, the distance of distinct vision.

(c) A person suffering from long-sightedness can see clearly far objects but the close objects appear to be blurred. This defect can be corrected by using a convex lens of a proper focal length.

Section-C
(Answer any two questions)

Question 8.
(a) (i) What is meant by ‘Quantization of charge’ ?
(ii) In Thomson’s experiment, prove that the ratio of chage to the mass (e/m) of an electron is given
\(\frac{e}{m}=\frac{1}{2 \mathrm{V}} \cdot \frac{\mathrm{E}^{2}}{\mathrm{B}^{2}}\)
where the terms have their usual meaning. [3]

(b) In a photoelectric cell, a retarding potential of 0.5 V is required to block the movement of electrons from the cathode when monochromatic light of wavelength 400 nm is incident on its surface. Find the work function of the material of the cathode. [3]

(c) Name a phenomenon or an experiment which proves : [2]
(i) Particle nature of electromagnetic radiations. [2]
(ii) Wave nature of particles.
(Description of the phenomenon/experiment is not required).
Answer:

(c) (i) The phenomenon of photoelectric effect proves the particle nature of electromagnetic radiations.
(ii) Davisson-Germer experiment proves the wave nature of particles.

Question 9.
(a) (i) State the postulate of Bohr’s theory regarding : [3]

• Angular momentum of an electron.
• Emission of a photon.

(ii) Total energy of an electron orbiting around the nucleus of an atom is always negative. What is the significance of this ?

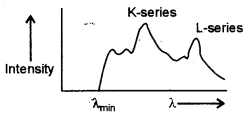
(b) (i) Draw a labelled graph showing variation of relative intensity of X-rays versus their wavelength λ. Mark λ_min on the graph.
(ii) State how the value of λ_min can be varied. [3]

(c) Half life of a certain radioactive substance is 6 hours. If you had 3.2 kg of this substance in the beginning, how much of it will disintegrate in one day ? [2]
Answer.
(a) (i) Postulates of Bohr’s theory:
(1) According to angular momentum postulate, electron can revolve only in those orbits around the nucleus in which its angular momentum is an integral multiple of h/2π
i. e., \(m v r=n \frac{h}{2 \pi}\)

(2) The emission or absorption of energy takes place when an electron jumps from one excited state to the other. If the energy state E₂ to the energy state E₁, the frequency of the emitted radiation is given by
E₂-E₁ =h_v
(ii) If the total energy of an electron orbiting around the nucleus is – ve, it implies that the electron is not free but is bound to the nucleus. To make the electron, energy must be supplied from an external source.

(b) (i) The relation between the intensity of X-rays emitted and the corresponding wavelength is as shown below


Question 10.
(a) (i) What is the significance of binding energy per nucleon of a nucleus ?
(ii) In a certain star, three alpha particles undergo fusion in a single reaction to form \(_{6}^{12} \mathrm{C}\) nucleus. Calculate the energy released in this reaction in MeV
\(\text { Given } : m\left(\begin{array}{l}{4} \\ {2}\end{array} \mathrm{He}\right)=4 \cdot 002604 \mathrm{u} \text { and } m(\stackrel{12}{6} \mathrm{C})=12 \cdot 000000 \mathrm{u} \text { . }\)  [3]

(b) Show by drawing labelled diagrams, the nature of output voltages in case of: [3]
(i) A half wave rectifier.
(ii) A frill wave rectifier. .
(iii) An Amplifier,
(In each case, input is an ac voltage)
Circuit diagrams of these devices are not required.

(c) Identify the logic gate whose truth table is given below and draw its symbol: [2]


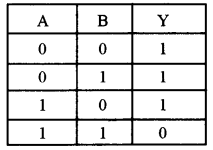
Answer:
(i) Binding energy per nucleon of a nucleus is defined as the average energy required to remove a nucleon from the nucleus. More the binding energy per nucleon more stable is the nucleus.

ISC Class 12 Physics Previous Year Question Papers