ISC Maths Question Paper 2010 Solved for Class 12

ISC Maths Previous Year Question Paper 2010 Solved for Class 12

Time Allowed: 3 Hours
Maximum Marks: 100

(Candidates are allowed additional 15 minutes for only reading the paper. They must NOT start writing during this time.)

• The Question Paper consists of three sections A, B and C.
• Candidates are required to attempt all questions from Section A and all questions either from Section B or Section C.
• Section A: Internal choice has been provided in three questions of four marks each and two questions of six marks each.
• Section B: Internal choice has been provided in two questions of four marks each.
• Section C: Internal choice has been provided in two questions of four marks each.
• All working, including rough work, should be done on the same sheet as, and adjacent to the rest of the answer.
• The intended marks for questions or parts of questions are given in brackets [ ].
• Mathematical tables and graph papers are provided.

Section – A
(All questions are compulsory in this part)

Question 1.
(i) If the matrix \(A=\left[\begin{array}{rrr}{6} & {x} & {2} \\ {2} & {-1} & {2} \\ {-10} & {5} & {2}\end{array}\right]\) is a singular matrix, find the value of x. [3]
(ii) Solve: \(\cos ^{-1}\left[\sin \left(\cos ^{-1} x\right)\right]=\pi / 3\) [3]
(iii) Show that the liney = x + √7 touches the hyperbola 9x² – 16y² = 144. [3]
(iv) Evaluate: \(\lim _{x \rightarrow \pi / 2}\left[x \tan x-\frac{\pi}{2} \sec x\right]\) [3]
(v) Evaluate: \(\int \frac{x}{(x+1)^{2}} d x\) [3]
(vi) Evaluate: \(\int_{-3}^{3}|x+2| d x\) [3]
(vii) A fair die is thrown once. What is the probability that either an even number or a number greater than three will turn up? [3]
(viii) If the regression equation of x on y is given by mx – y + 10 = 0 and the equation ofyonx is given by -2x + 5y = 14, determine the value of ‘m’ if the coefficient of correlation between x and y is \(\frac{1}{\sqrt{10}}\) [3]
(ix) If 1, ω, ω² are the three cube roots of unity, then simplify: (3 + 5ω + 3ω²)² (1 + 2ω + ω²) [3]
(x) Solve the differential equation: cosec³x dy – cosec y dx = 0 [3]
Answer:

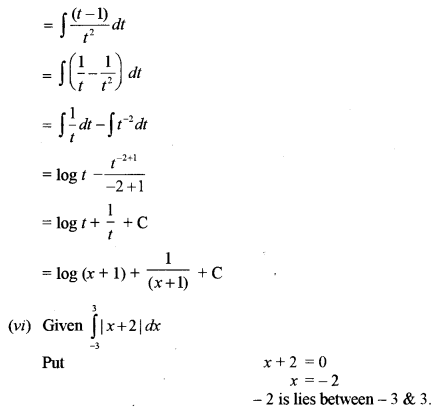
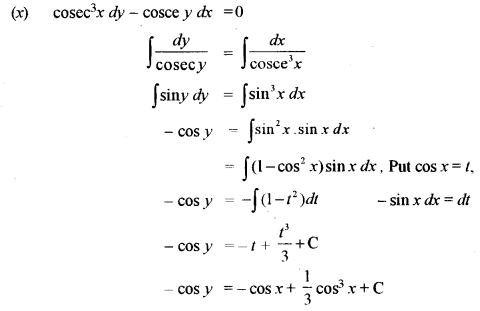
Question 2.
(a) By using properties of determinants, prove that the determinant \(\left|\begin{array}{ccc}{a} & {\sin x} & {\cos x} \\ {-\sin x} & {-a} & {1} \\ {\cos x} & {1} & {a}\end{array}\right|\) is independent of x. [5]
(b) Using matrix method, solve the following equations: [5]
5x + 3y + z = 16
2x + y + 3z = 19
x + 2y + 4z = 25
Answer:

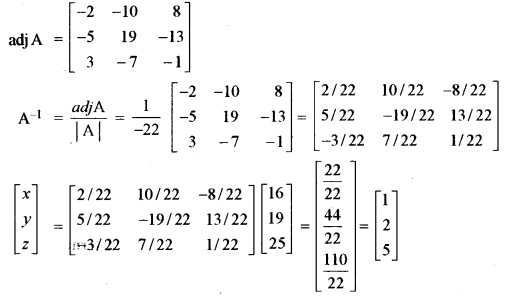
Question 3.
(a) Using Rolle’s theorem, find a point on the curvey = sinx + cos x – 1, \(x \in\left[0, \frac{\pi}{2}\right]\) tangent is parallel to the x- axis. [5]
(b) Find the equation of the parabola whose focus is (-1, -2) and the equation of the directrix is given by 4x – 3y + 2 = 0. Also find the equation of the axis. [5]
Answer:

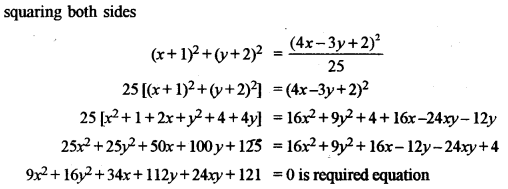
Question 4.
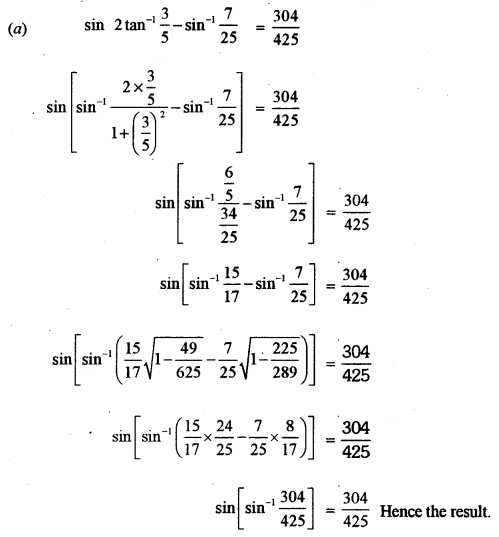
(a) Prove that: [5]
\(\sin \left[2 \tan ^{-1} \frac{3}{5}-\sin ^{-1} \frac{7}{25}=\frac{304}{425}\right]\)
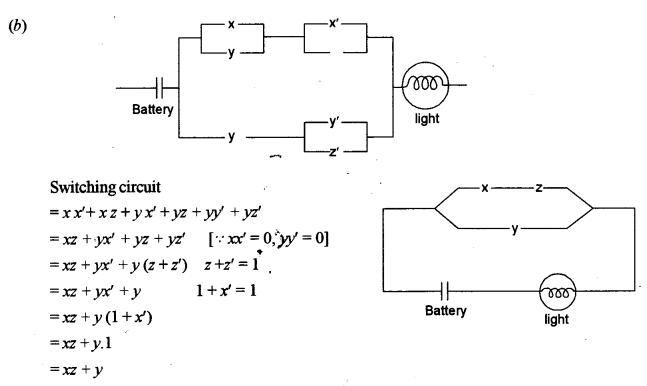
(b) x, y and z represent three switches in an ‘ON’ position and x’ y ‘and z’ represent the same three switches in an ‘OFF’ position. Construct a switching circuit representing the polynomial (x + y) (x’ + z) + y(y’ + z’).
Using the laws of Boolean Algebra, show that the above polynomial is equivalent to xz + y and construct an equivalent switching circuit. [5]
Answer:

Question 5.
(a) Using a suitable substitution, find the derivative of \(\tan ^{-1} \sqrt{\frac{a-x}{a+x}}\) with respect to x. [5]
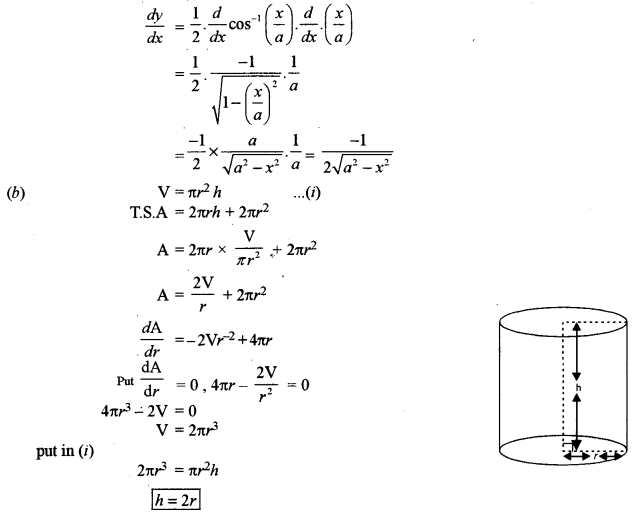
(b) A closed right circular cylinder has volume \(\frac{539}{2}\) cubic units. Find the radius and the height of the cylinder so that the total surface area is minimum. [5]
Answer:

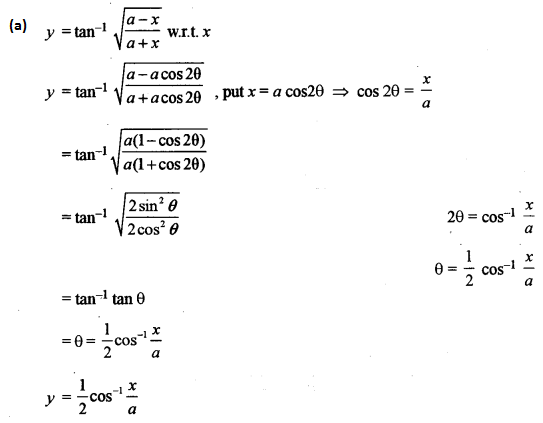
Question 6.
(a) Evaluate: [5]
\(\int \frac{2 \sin 2 \theta-\cos \theta}{6-\cos ^{2} \theta-4 \sin \theta} d \theta\)
(b) Draw a rough sketch of the curve y = x² – 5x + 6 and find the area bounded by the curve and the x-axis. [5]
Answer:

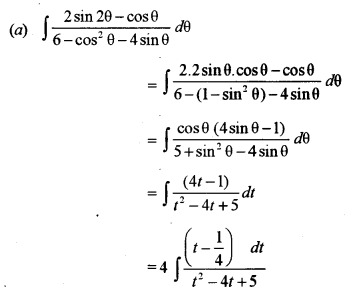
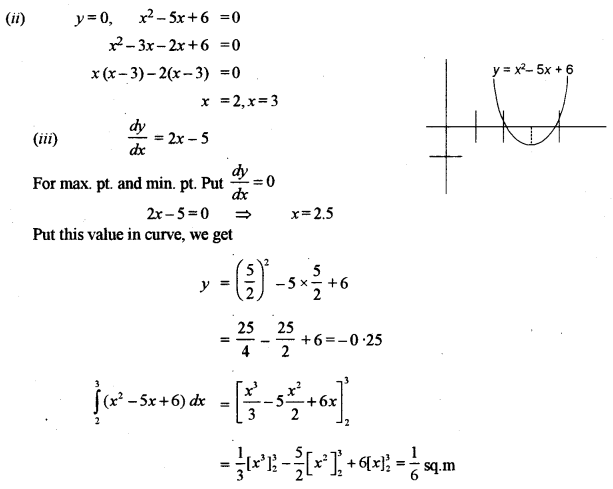
Question 7.
(a) Find the equations of the two lines of regression for the following observations: [5]
(3, 6), (4, 5), (5, 4), (6, 3), (7, 2)
Find an estimate of y for x = 2.5
(b) Calculate Spearman’s coefficient of rank correlation from the following data and interpret the result: [5]

Answer:

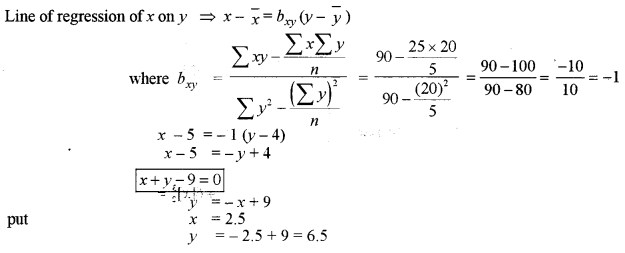
Question 8.
(a) Akhil and Vijay appear for an interview for two vacancies. The probability of Akhil’s selection is \(\frac { 1 }{ 4 }\) and Vijay’s selection is \(\frac { 2 }{ 3 }\). Find the probability that only one of them will be selected. [5]
(b) There are two bags. One bag contains six green and three red balls. The second bag contains five green and four red balls. One ball is transferred from tire first bag to the second bag. Then one ball is drawn from the second bag. Find the probability that it is a red ball. [5]
Answer:

Question 9.
(a) Solve the differential equation: (y + log x) dx – x dy = 0, given that y = 0, when x = 1. [5]
(b) Find the locus of a complex number z = x + iy, satisfying the relation |3z – 4i| ≤ |3z + 2|. [5]
Illustrate the locus in Argand’s plane.
Answer:

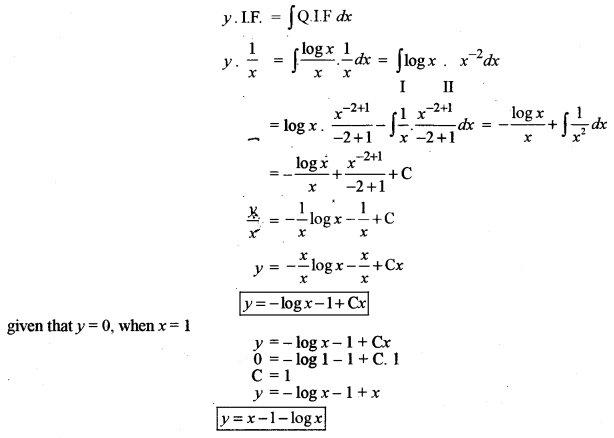
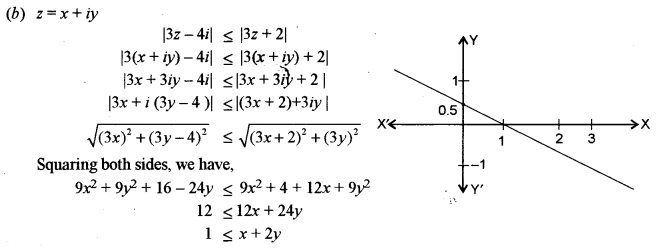
Section – B

Question 10.
(a) Find the value of λ for which the four points with position yeptors \(2 \hat{i}+5 \hat{j}+\hat{k},-\hat{j}-4 \hat{k}\), \(3 \hat{i}+\lambda \hat{j}+8 \hat{k} \text { and }-4 \hat{i}+3 \hat{j}+4 \hat{k}\) are coplaner, then find λ. [5]
(b) In any ∆ABC, prove by vector method that \(\cos B=\frac{c^{2}+a^{2}-b^{2}}{2 c a}\) [5]
Answer:

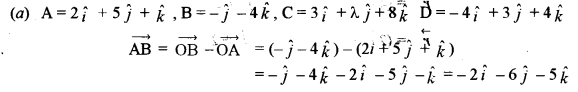
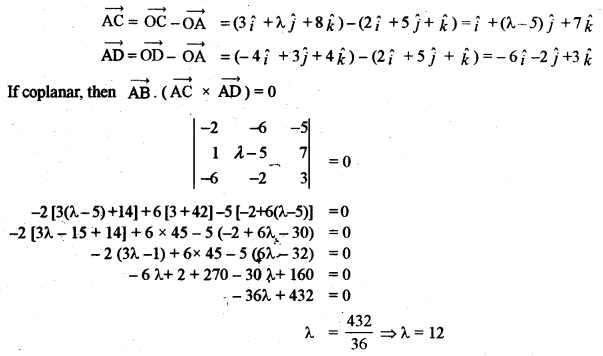
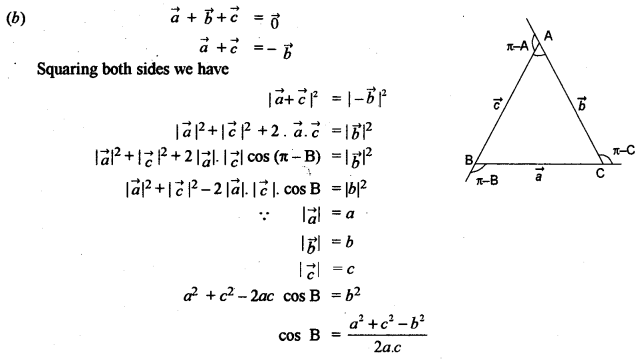
Question 11.
(a) Find the shortest distance between the lines whose vector equations are:
\(\vec{r}=(4 \hat{i}-\hat{j}+2 \hat{k})+\lambda(\hat{i}+2 \hat{j}-3 \hat{k}) \text { and } \vec{r}=(2 \hat{i}+\hat{j}-\hat{k})+\mu(\hat{3} \hat{i}+2 \hat{j}-4 \hat{k})\)
(b) Find the equation of the plane passing through the line of intersection of the planes x + 2y + 3z – 4 = 0 and 3z – y = 0 and perpendicular to the plane 3x + 4y – 2z + 6 = 0. [5]
Answer:

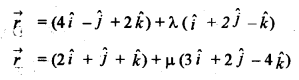
Question 12.
(a) A factory has three machines A, B, C producing 1500, 2500 and 3000 bulbs per day respectively. Machine A produces 1.5% defective bulbs, machine B produces 2% defective bulbs and machine C produces 2.5% defective bulbs. At the end of the day, abulb is drawn at random and is found to be defective. What is the probability that this defective bulb has been produced by machine B? [5]
(b) Five bad eggs are mixed with 10 good ones. If three eggs are drawn one by one with replacement, find the probability distribution of the number of good eggs drawn. [5]
Answer:
(a) Total daily production of bulb = 1500 + 2500 + 3000 = 7000 units
E₁, E₂, E₃ be the events of selecting a bulb produced by the three machine A, B and C

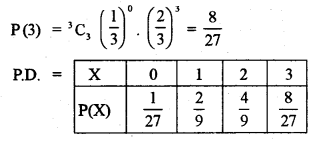
Section – C

Question 13.
(a) A company produces two types of items, P and Q. Manufacturing of both items requires the metals gold and copper. Each unit of item P requires 3 gms of gold and 1 gm of copper while that of item Q requires 1 gm of gold and 2 gms of copper. The company has 9 gms of gold and 8 gms of copper in its store. If each unit of item P makes a profit of Rs 50 and each unit of item Q makes a profit of Rs 60, determine the number of units of each item that the company should produce to maximize profit. What is the maximum profit? [5]
(b) At the beginning of each quarter, a sum of Rs 1,500 is deposited into a savings account that pays 12% per annum compounded quarterly. Find the amount in the account at the end of four years. [5]
Answer:

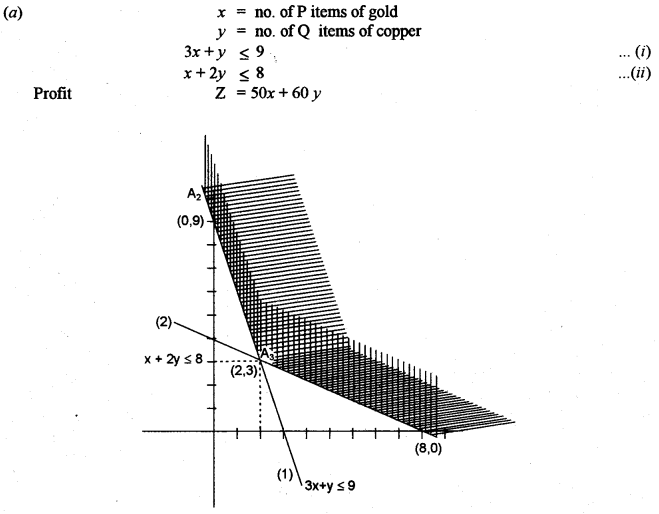
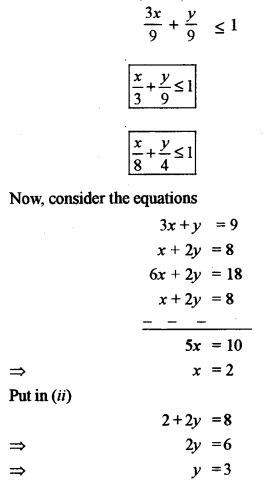
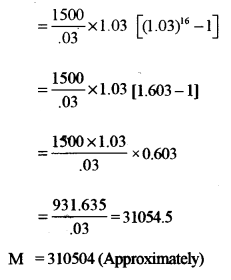
Question 14.
(a) A bill of exchange for Rs 722 was drawn on the 3rd April 2009, payable three months after date. It was discounted on 15th April 2009 at 4.75% per annum. What was the discounted value of the gift? [5]
(b) The average cost function AC for a commodity is given by \(\mathrm{AC}=x+5+\frac{36}{x}\) in terms of output x. Find the:
(i) Total cost and the marginal cost as the functions of x. [5]
(ii) Output for which AC increases.
Answer:

Question 15.
(a) The index number for the following data, for the year 2008, taking 2004 as the base year was found to be 116. The simple aggregate method was used for calculation. Find the numerical values of x and y if the sum of the prices in the year 2008 is Rs. 203. [5]

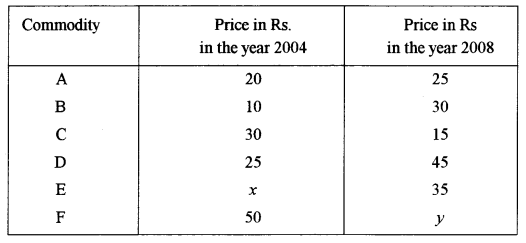
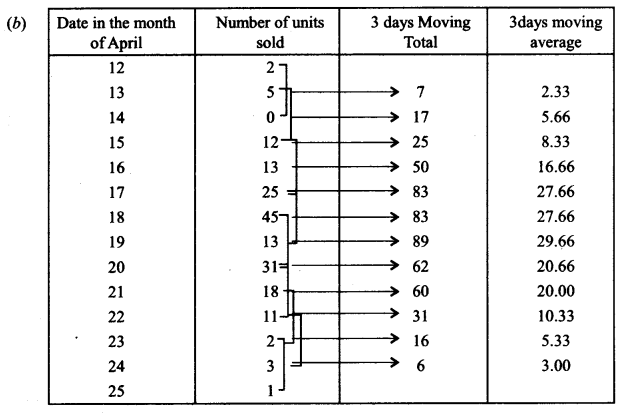
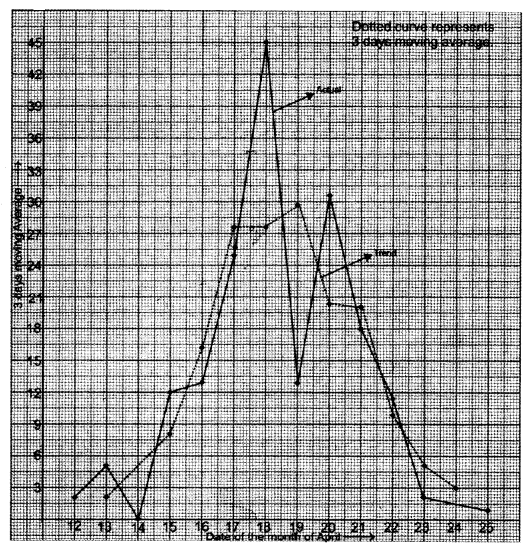
(b) Consider the following data: [5]

Calculate three days moving averages and display these and the original figures on the same graph.
Answer:

ISC Class 12 Maths Previous Year Question Papers