Exponential Functions

Exponential Functions

Definition:
The exponential function with base b is defined by f^–(x) = b^x  

where b > 0  , b≠1

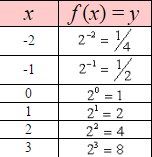
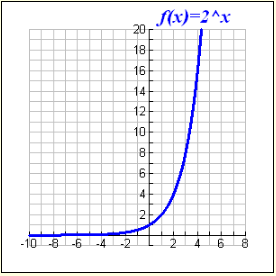
Most exponential graphs resemble this same shape.
This graph is very, very small on its left side and is extremely close to the x-axis. As the graph progresses to the right, it starts to grow faster and faster and shoots off the top of the graph very quickly, as seen at the right.

In a straight line, the “rate of change” remains the same across the graph. In these graphs, the “rate of change” increases or decreases across the graphs.

Characteristics:

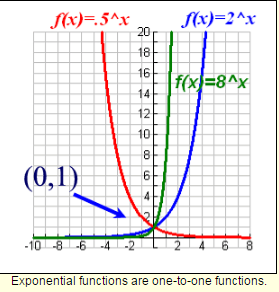
Such exponential graphs of the form f(x) = b^x have certain characteristics in common:

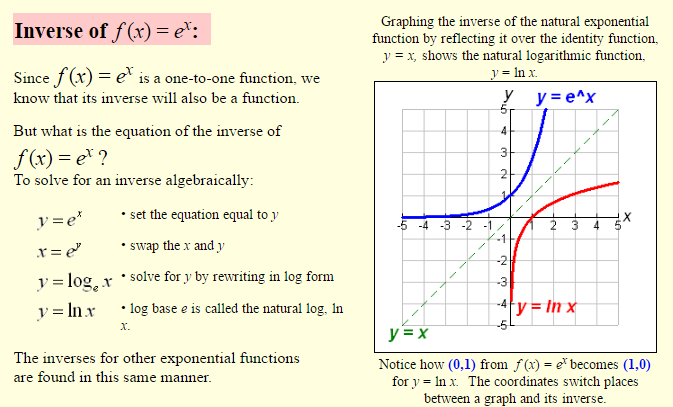
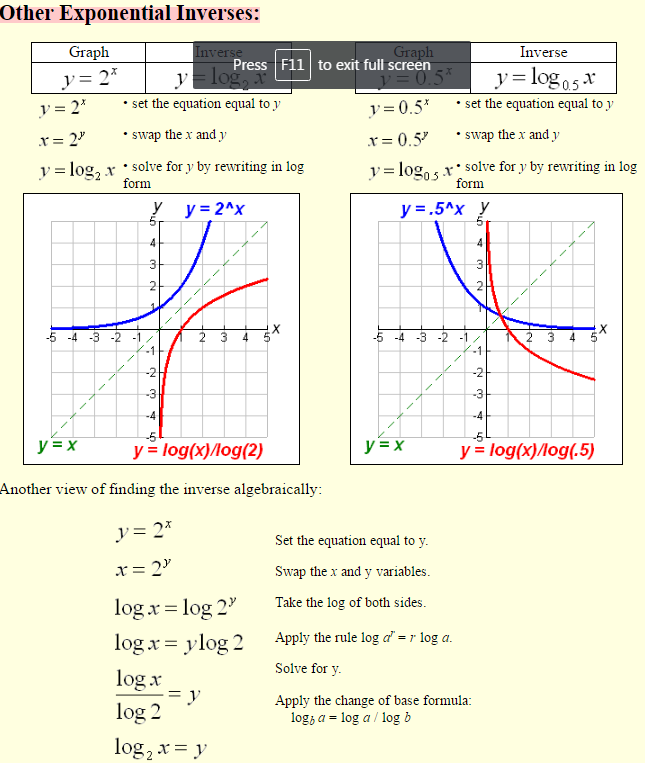
Exponential functions are one-to-one functions. • graph crosses the y-axis at (0,1)
• when b > 1, the graph increases

• when 0 < b < 1, the graph decreases

• the domain is all real numbers

• the range is all positive real numbers (never zero)

• graph passes the vertical line test – it is a function

• graph passes the horizontal line test – its inverse is also a function.

• graph is asymptotic to the x-axis – gets very, very close to the x-axis but does not touch it or cross it.

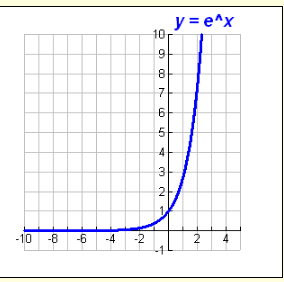
Natural Exponential Function:

The function defined by f (x) = e^x is called the natural exponential function.

(e is an irrational number, approximately 2.71828183, named after the 18th century Swiss mathematician, Leonhard Euler .)

Notice how the characteristics of this graph are similar to those seen above.

This function is simply a “version” of
where b >1.