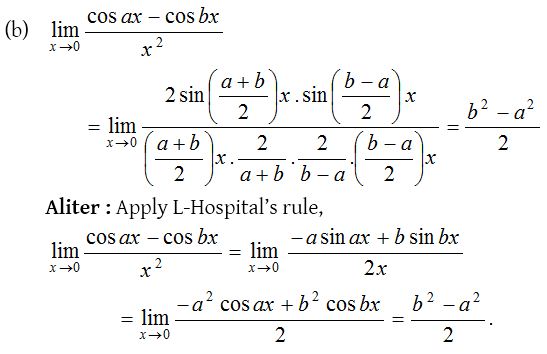Evaluating Limits
Methods of evaluation of limits
We shall divide the problems of evaluation of limits in five categories.
(1) Algebraic limits:
Let f(x) be an algebraic function and ‘a’ be a real number. Then ![]() is known as an algebraic limit.
is known as an algebraic limit.
- Direct substitution method: If by direct substitution of the point in the given expression we get a finite number, then the number obtained is the limit of the given expression.
- Factorisation method: In this method, numerator and denominator are factorised. The common factors are cancelled and the rest outputs the results.
- Rationalisation method: Rationalisation is followed when we have fractional powers (like \(\frac { 1 }{ 2 } ,\frac { 1 }{ 3 }\) etc.) on expressions in numerator or denominator or in both. After rationalisation the terms are factorised which on cancellation gives the result.
- Based on the form when x → ∞: In this case expression should be expressed as a function 1/x and then after removing indeterminate form, (if it is there) replace 1/x by 0.
(2) Trigonometric limits:
To evaluate trigonometric limit the following results are very important.
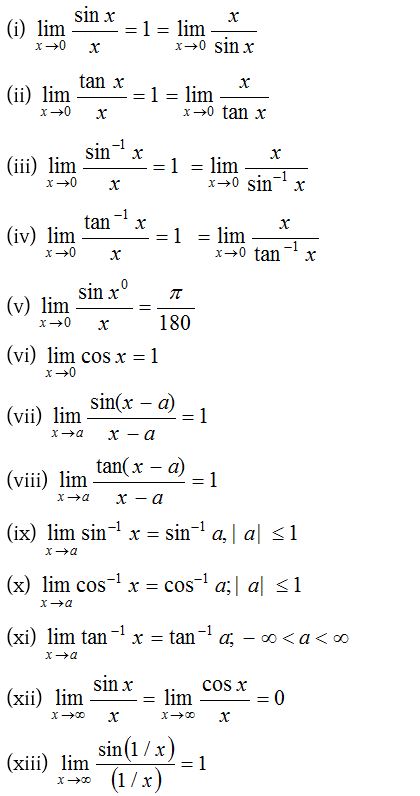
(3) Logarithmic limits:
To evaluate the logarithmic limits we use following formulae:
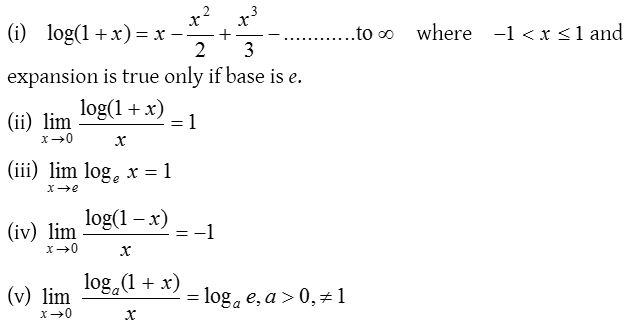
(4) Exponential limits:
(i) Based on series expansion:
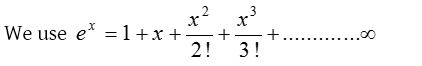
To evaluate the exponential limits we use the following results:
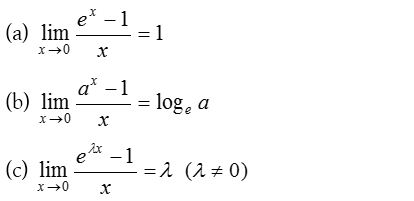
(ii) Based on the form 1∞: To evaluate the exponential form 1∞ we use the following results.
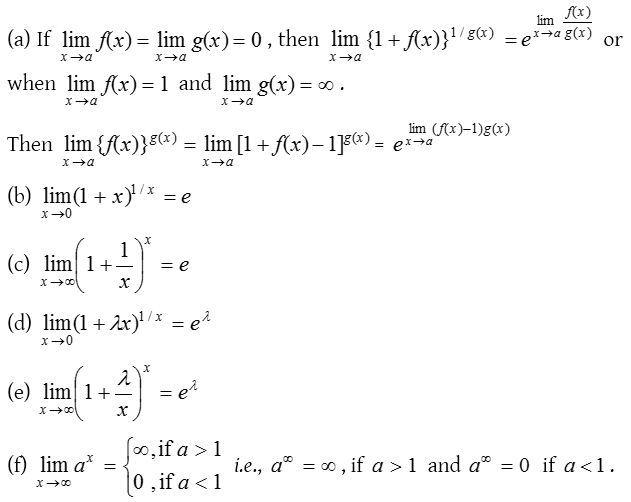
(5) L-Hospital’s rule:
If f(x) and g(x) be two functions of x such that

Sometimes it may be necessary to repeat this process a number of times till our goal of evaluating limit is achieved.
Evaluating Limits Problems with Solutions
1.
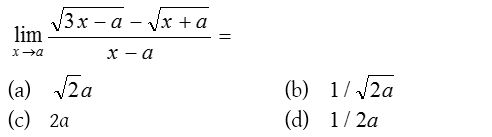
Solution:
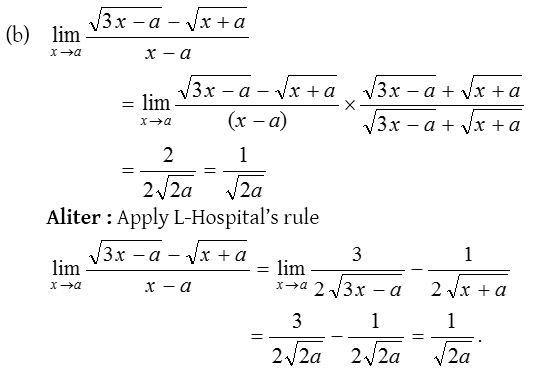
2.
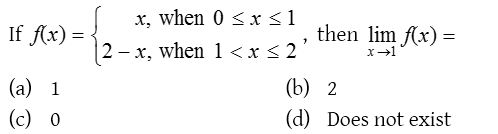
Solution:
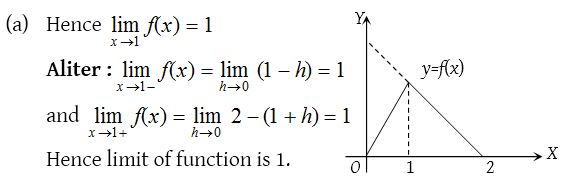
3.

Solution:
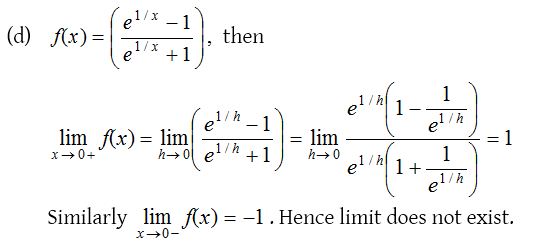
4.

Solution:
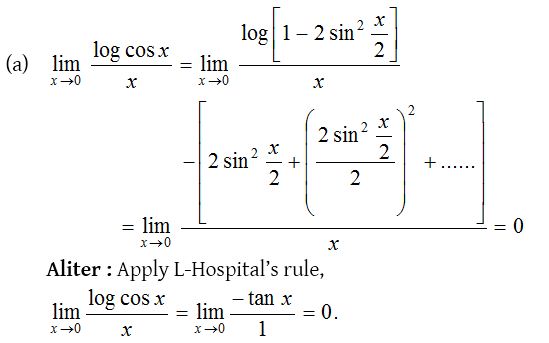
5.

Solution:
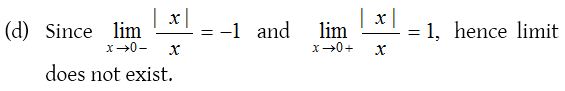
6.
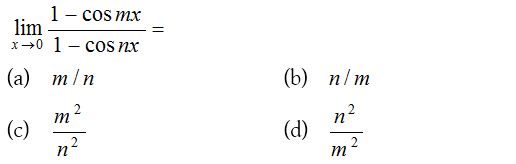
Solution:
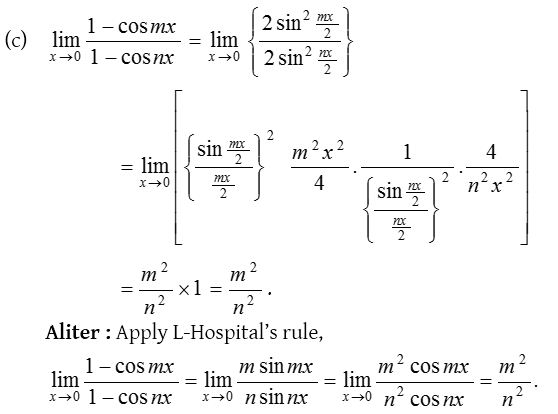
7.

Solution:
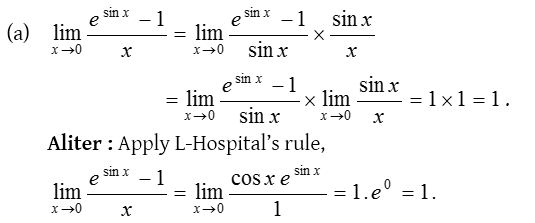
8.
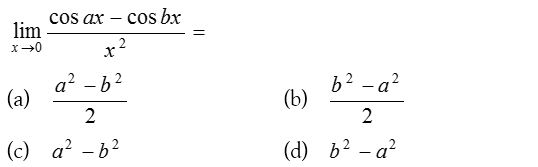
Solution: