Equation of Circles
Let’s review what we already know about circles.
Definition: A circle is a locus (set) of points in a plane equidistant from a fixed point.

Now, if we “multiply out” the above example (x-2)2 + (y+5)2 = 9 we will get:
(x-2)2 + (y+5)2 = 9
(x2-4x+4) +( y2+10y+25) = 9
x2-4x+4+ y2+10y+25 = 9
x2+ y2-4x+10y+20= 0
x2+y2+Cx+Dy+E = 0
When multiplied out, we obtain the “general form” of the equation of a circle. Notice that in this form we can clearly see that the equation of a circle has both x2 and y2 terms and these terms have the same coefficient (usually 1).
When the equation of a circle appears in “general form”, it is often beneficial to convert the equation to “center-radius” form to easily read the center coordinates and the radius for graphing.

Examples:
1. Convert x2+ y2-4x-6y+8= 0 into center-radius form.
This conversion requires use of the technique of completing the square.
We will be creating two perfect square trinomials within the equation.
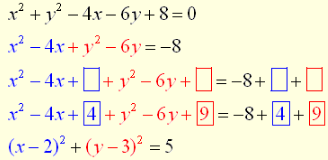
- Start by grouping the x related terms together and the y related terms together. Move any numerical constants (plain numbers) to the other side.
- Get ready to insert the needed values for creating the perfect square trinomials. Remember to balance both sides of the equation.
- Find each missing value by taking half of the “middle term” and squaring. This value will always be positive as a result of the squaring process.
- Rewrite in factored form.
You can now read that the center of the circle is at (2, 3) and the radius is /5
2. How do the coordinates of the center of a circle relate to C and D when the equation of the circle is in the general form x2+ y2+Cx+Dy+E = 0.
Let’s make some observations. Re-examine our previous equations in general form and center-radius form. Do you see a relationship between the center coordinates and C and D?

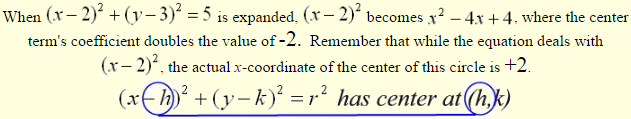
3. Write the equation of a circle whose diameter has endpoints (4, -1) and (-6, 7).

4. Write the equation for the circle shown below if it is shifted 3 units to the right and 4 units up.
A shift of 3 units to the right and 4 units up places the center at the point (3, 4). The radius of the circle can be seen from the graph to be 5.
Equation:(x-3)2 + (y-4)2 = 25
5. Convert 2x2+ 2y2+6x-8y+12= 0 into center-radius form.
Whoa!!! This equation looks different. Are we sure this is a circle???
In this equation, both the x and y terms appear in squared form and their coefficients (the numbers in front of them) are the same. Yes, we have a circle here! We will, however, have to deal with the coefficients of 2 before we can complete the square.
